一.行列式
1.利用行列式的性質進行簡化
(1)重要行列式
主對角線,副對角線(不要忘了-1的次數),拉普拉斯展開(副對角線是m*n),范德蒙
(2)行列式展開定理
每一行/列的元素乘以它對應的代數余子式
擴展:拉普拉斯展開定理,可以按照任意行和列數進行展開,行列式的值=|A|* |B|*(-1)^(按哪幾行和列展開的行和 和 列和相加)
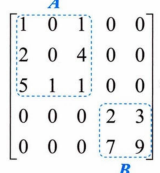
上面的矩陣就是=|A|* |B|*(-1)^(4 + 5 + 4 + 5) = 6
(3)加邊法

遇到如圖所示得行列式可以使用加邊法(實質還是行列式的展開定理)
方法詳解:在整個行列式的左上角加一行和一列,左上角的元素是1(加其他位置也可以,要滿足行列式的展開定理就行),讓他的一行/一列等于0(除了左上角的元素),一列等于(a1,a2,a3,a4)^T,這樣就可以使用第一列/第一行將行列式里的aiaj都消掉,最后轉化成爪形行列式
(4)遞推
高階到低階:遞推;低階到高階:歸納;
擴展:二階差分方程

Dn和Dn-2差2階就叫二階差分方程
解法:和求二階微分方程一樣,先算找特征方程算特征根解出來r1=α,r2=β
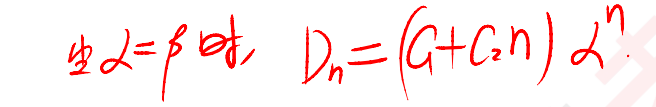

(5)三對角矩陣

2.代數余子式求和
(1)代數余子式定義
(2)展開定理
(3)A*(這里包含了A的所有代數余子式)
3.抽像形行列式的計算
(1)行列式的性質
(2)行列式的公式
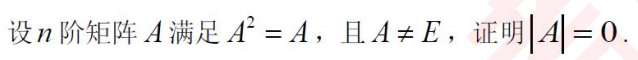
經典錯誤1:不能由行列式不等于E,得出行列式的值不為1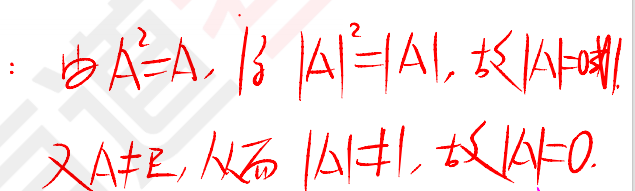
經典錯誤2:A≠E,的不出|A-E|不等于0
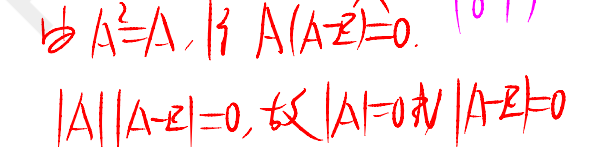

解法1:可以使用逆
解法2:秩
解法3:方程組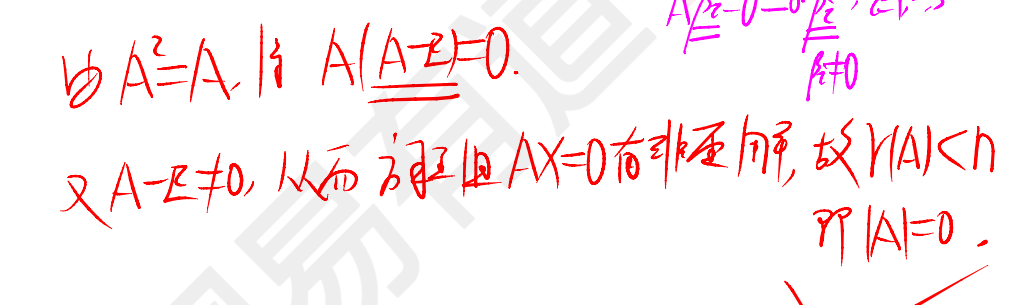
解法4:特征值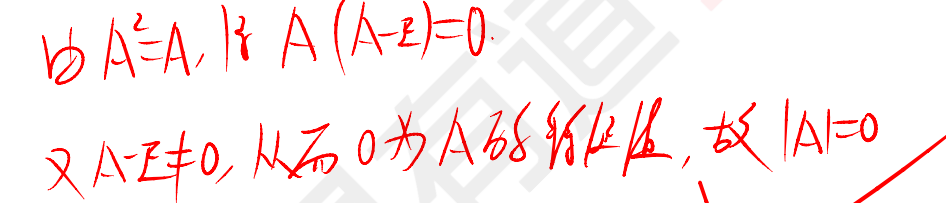
(4)總結AB=0:
a.r(A)+r(B)<=n
b.B的列向量都是Ax=0的解
c.A的行向量與B的列向量正交
d.若A為n階方陣,則B的非零列向量均為A的特征值
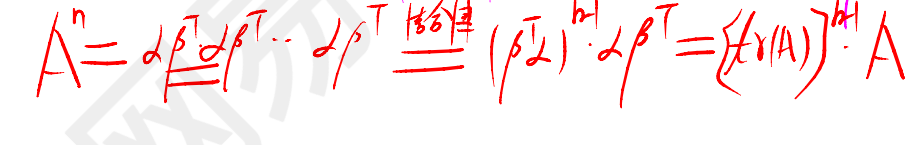
)








)


)






)