入門
久聞并查集的大名,今天來一探究竟,到底什么是并查集,并查集有什么用?
并查集(Disjoint Set Union, DSU)是一種處理不相交集合的合并及查詢問題的數據結構。
其實并查集的作用主要就有兩個:
1、將兩個元素添加到同一個集合
2、判斷兩個元素是否在同一個集合內
碰到諸如此類的問題,就可以條件反射的去想到用并查集來解決了。
首先就是預處理的操作了只需要將所有的點連向自己即可:
void pre_handle()
{for(int i=0;i<n;i++) father[i] = i;
} 然后就是添加函數和判斷函數了,這兩個函數都基于查找函數,要首先查找到兩個點的根節點是誰
普通的查找函數:查找函數是基于遞歸來實現的,就是不斷的遞歸去找父節點的父節點知道根節點
int find(int x)
{if(father[x] == x) return x;return find(father[x]);
}但是這樣一直遞歸無疑是一個非常浪費時間的過程,每次查找一個點的根節點的時候都要從這個點開始遞歸到根節點,其實這個過程中做了很多重復的東西,在一個點遞歸完之后,他的所有父節點是不就就無需再遞歸了呢,所以就要考慮能不能把路徑壓縮,其實只需要在遞歸的過程中,將每個點的父節點都存為根節點,這樣在下一次查找的時候,既可以直接根據這個點存的值直接找到該點的根節點了,比如一開始的1->2->3->4 當find(1)的時候在遞歸的過程中就變為了1->4, 2->4, 3->4 這樣在下一次找2的根節點的時候就直接遞歸一次即可返回4,這個操作在較深的圖中是很有用的!
int find(int x)
{if(father[x] == x) return x;father[x] = find(father[x]);//直接將根節點賦值給x的父節點 相當于深度變為了兩層return father[x];
}這樣是不是很妙呢?有了find函數,接下來的添加(join)和判斷(is_same)函數就很容易實現了。
join:
void join(int x,int y)
{x = find(x);//x直接存x的根節點y = find(y);//y同樣存y的根節點if(x==y) return ;//如果x和y的根節點相同就說明本來就在同一個集合內father[x] = y;//讓x的根節點指向y的根節點 就說明此時兩個集合已經聯通了
}is_same:
bool is_same(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}理論完成,下面開始做幾道題來練練手吧!
尋找存在的路徑?
題目鏈接:尋找存在的路徑
這是并查集的基礎模板的應用,按要求將聯通的兩個點加入到同一個集合中即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 110;
vector<int> father(N);
int n,m;
void pre_handle()
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;father[x] = find(father[x]);return father[x];
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;//兩個集合聯通
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
void solve()
{cin>>n>>m;pre_handle();for(int i=1;i<=m;i++){int u,v;cin>>u>>v;join(u,v);}int u,v;cin>>u>>v;if(is(u,v)) cout<<"1"<<endl;else cout<<"0"<<endl;
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
冗余的邊?
題目鏈接:冗余的邊
這道題雖然是看著像一個復雜的樹或圖問題,其實本質上就是判斷當前的邊所連接的兩個點之前可達不可達,如果可達(聯通)的話那么此時的邊就是冗余的了,又因為聯通無環無向圖就是一顆樹所以只有一條冗余的邊。那么只需要用并查集去判斷是否可達(在一個集合內)即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 1010;
vector<int> father(N);
int n;
int ans1,ans2;
void pre_handle()
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;father[x] = find(father[x]);return father[x];
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;//兩個集合聯通
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
void solve()
{cin>>n;pre_handle();for(int i=1;i<=n;i++){int u,v;cin>>u>>v;if(is(u,v))//只要u和v在同一個集合中(可達 聯通)就說明此時的邊冗余了{ans1 = u;ans2 = v;}else join(u,v);}cout<<ans1<<" "<<ans2<<endl;
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
冗余的邊II?
題目鏈接:冗余的邊II
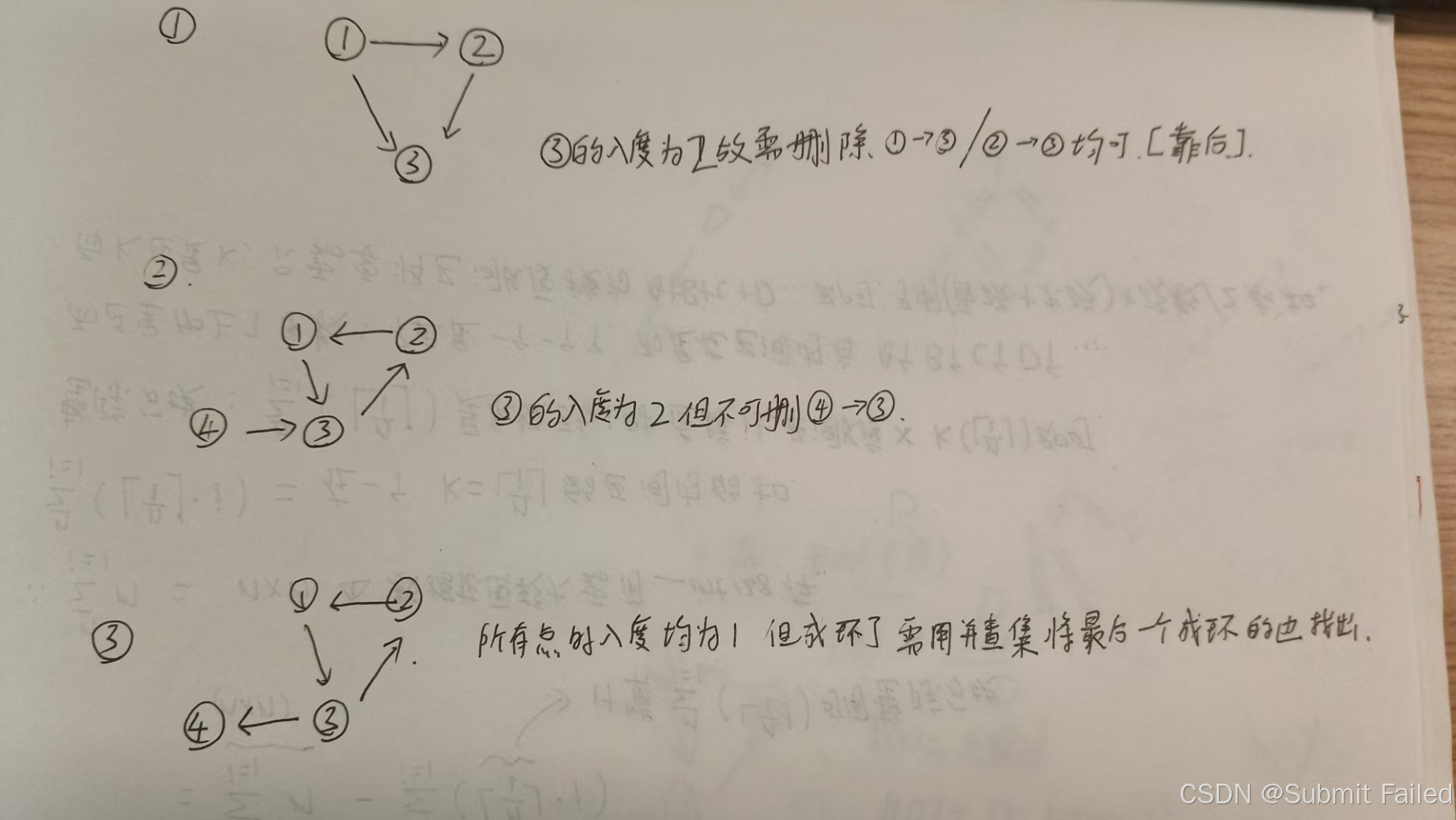
這道題原本是一個有向樹,因為多了一條冗余的邊導致成為了一個圖,所以我們就要判斷哪些情況是導致冗余的原因,大體上分為兩種
1.有向樹的性質就是除了根節點的入度為0,其他的節點入度為1,入度為2就說明不是樹了
2.入度也可能都是1,但是如果構成環了也就不是樹了
但是第一種情況又可以細分,入度為2可能只有其中一條邊是冗余的(入度為0的根節點與其相連的時候 這條邊就不是一個冗余的邊)所以要在入度為2的時候判斷一下是否能刪
可以利用并查集來判斷是否有環!
題目特殊條件:
圖是由"有向樹添加一條邊"構成的
這意味著原始結構是一棵有向樹(n-1條邊)
添加一條邊后(共n條邊),只可能產生兩種違規情況:
a) 某個節點入度變為2
b) 形成一個環并查集的適用性:
雖然并查集通常用于無向圖,但這里我們關注的是"連接性"而非方向
判斷是否有環時,方向不重要(有向環必然包含無向環)
判斷連通性時,方向也不重要(我們只需知道節點是否相連)
方向信息的處理:
入度統計單獨處理(用
indegree數組)并查集只負責檢測環和連通性
兩個部分各司其職,共同解決問題
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 1010;
vector<int> father(N),indegree(N,0),a;//定義并查集數組 入度數組 以及入度為2的數組
vector<pii> e(1);//存所有的兩兩有連接的邊 不需要建樹 只需要用入度和并查集統計邊即可
int n;
void init()//初始化并查集
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;return father[x] = find(father[x]);
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
bool istree(int x)//刪除x這條邊之后是否是一棵樹
{//判斷連通性時,方向并不重要(我們只需知道節點是否相連)init();for(int i=1;i<=n;i++){if(i == x) continue;if(is(e[i].fi,e[i].se)) return false;//成環了 不是有向樹了join(e[i].fi,e[i].se);}return true;
}
void solve()
{cin>>n;init();for(int i=1;i<=n;i++){int u,v;cin>>u>>v;e.push_back({u,v});indegree[v]++;}for(int i=1;i<=n;i++){if(indegree[e[i].se] == 2) a.push_back(i);//將導致入度為2的邊的編號存入}if(a.size()>0)//size==2{if(istree(a[1]))//因為要輸出標準輸入中靠后的一個 所以先判斷a[1]cout<<e[a[1]].fi<<' '<<e[a[1]].se<<endl;else//如果刪除a[1]這條邊的話還是一個圖 那么就一定是另一條邊了(因為只會多出來一條邊)cout<<e[a[0]].fi<<' '<<e[a[0]].se<<endl;}else//第三種情況{init();//找冗余的邊 用并查集 判斷成環的那條邊//判斷是否有環時,方向并不重要(有向環必然包含無向環)for(int i=1;i<=n;i++){if(is(e[i].fi,e[i].se)){cout<<e[i].fi<<' '<<e[i].se<<endl;return ;}elsejoin(e[i].fi,e[i].se);}}
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
總之,并查集應用于無向圖中,目的是看兩個點是否聯通或者兩個集合是否聯通以及將兩個點加入到同一個集合當中構成聯通性。?
這樣就將并查集的兩個主要作用給介紹完了,期待后續的迪杰斯特拉算法吧!

















)
和郵箱(Email)的特定彈窗)
