圖機器學習(5)——無監督圖學習
- 0. 前言
- 1. 無監督圖嵌入
- 2. 矩陣分解
- 2.1 圖分解
- 2.2 高階鄰接保留嵌入
- 2.3 帶有全局結構信息的圖表示
- 3. skip-gram 模型
- 3.1 DeepWalk
- 3.2 Node2Vec
- 3.3 Edge2Vec
- 3.4 Graph2Vec
0. 前言
無監督機器學習是指訓練過程中不利用任何目標信息的一類算法。這類算法能夠自主發現數據中的聚類結構、潛在模式、異常特征等,適用于沒有先驗知識或標準答案的各類問題。與其他機器學習算法類似,無監督模型在圖表示學習領域得到了廣泛應用。它們為解決節點分類、社區發現等下游任務提供了有效工具。
本節將介紹主流的無監督圖嵌入方法。這些技術的核心目標是從給定圖中自動學習其潛在表示,同時保持圖結構的關鍵特征。具體而言,算法需要在不依賴人工標注的情況下,通過挖掘圖數據的內在規律,生成能夠反映原始圖拓撲特性的低維向量表示。
1. 無監督圖嵌入
圖是定義在非歐幾里得空間中的復雜數學結構。簡單來說,這意味著我們往往難以明確界定圖中元素的“鄰近性”——甚至“鄰近”這一概念本身都可能難以定義。以社交網絡圖為例:兩個用戶可能彼此相連,但特征卻截然不同——一個可能關注時尚與服飾,另一個則可能熱衷于體育和電子游戲。這種情況下,是否能認為他們“相近”?
正因為如此,無監督機器學習算法在圖分析中得到了廣泛應用。無監督機器學習是一類可以在不需要人工標注數據的情況下進行訓練的機器學習算法。這類模型通常僅利用鄰接矩陣和節點特征中的信息,而無需預先了解下游機器學習任務的具體內容。
最常用的技術方案是學習能夠保持圖結構的嵌入表示。這類表示通常通過優化設計,使其能夠重建節點間的成對相似性(例如鄰接矩陣)。這些技術具有一項重要特性:學習到的表示可以編碼節點或圖之間的潛在關系,從而幫助我們發現隱藏的復雜新模式。
目前已有多種無監督圖機器學習算法,這些算法可歸納為三大類:淺層嵌入方法、自編碼器以及圖神經網絡 (Graph Neural Network, GNN),如下圖所示:
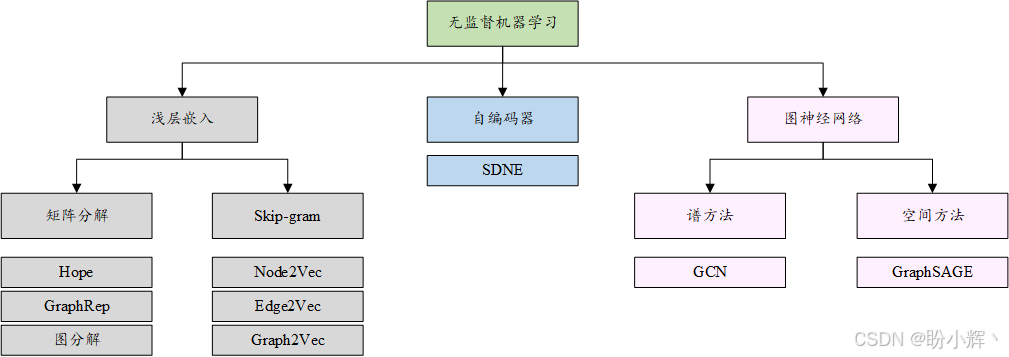
接下來,將介紹淺層嵌入算法背后的主要原理。淺層嵌入方法特指一類僅能學習并返回輸入數據嵌入值的算法,在本節中,我們將介紹其中的代表性算法,并通過實例演示其應用場景。
2. 矩陣分解
矩陣分解是一種廣泛應用于不同領域的通用分解技術。許多圖嵌入算法使用該技術來計算圖的節點嵌入。
我們將首先概述矩陣分解的基本原理,隨后重點介紹兩種使用矩陣分解構建圖的節點嵌入的算法,分別為圖分解 (Graph Factorization, GF) 和高階鄰近保留嵌入 (Higher-Order Proximity Preserved Embedding, HOPE)。
設輸入數據為矩陣 W∈Rm×nW ∈ ?^{m×n}W∈Rm×n,矩陣分解將其分解為 W≈V×HW ≈ V\times HW≈V×H 的形式,其中 V∈Rm×dV ∈ ?^{m×d}V∈Rm×d 稱為源矩陣,H∈Rd×nH ∈ ?^{d×n}H∈Rd×n 稱為豐度矩陣,ddd 代表生成嵌入空間的維度。矩陣分解算法通過最小化損失函數來學習 VVV 和 HHH 矩陣,該損失函數可根據具體求解問題進行調整。其通用形式采用 Frobenius 范數計算重構誤差,定義為 ‖W?V×H‖F2‖W - V\times H‖_F^2‖W?V×H‖F2?。
總體而言,所有基于矩陣分解的無監督嵌入算法都遵循相同原理:將圖結構表示的輸入矩陣分解為不同成分。各方法的主要區別在于優化過程中采用的損失函數——不同的損失函數能夠構建出突顯輸入圖特定性質的嵌入空間。
2.1 圖分解
圖分解算法 (graph factorization, GF) 是最早實現較好計算性能的節點嵌入模型之一。該算法基于前文所述的矩陣分解原理,對給定圖的鄰接矩陣進行分解。
設待計算節點嵌入的圖為 G=(V,E)G=(V,E)G=(V,E),其鄰接矩陣為 A∈R∣V∣×∣V∣A∈?^{|V|×|V|}A∈R∣V∣×∣V∣。該矩陣分解問題使用的損失函數 LLL 如下:
L=12∑(i,j)∈E(Ai,j?Yi,:Yj,:T)2+λ2∑i∣∣Yi,:∣∣2L=\frac 12\sum_{(i,j)\in E} (A_{i,j}-Y_{i,:}Y_{j,:}^T)^2+\frac {\lambda }2\sum_i||Y_{i,:}||^2 L=21?(i,j)∈E∑?(Ai,j??Yi,:?Yj,:T?)2+2λ?i∑?∣∣Yi,:?∣∣2
其中,(i,j)∈E(i,j)∈E(i,j)∈E 表示圖 GGG 中的一條邊,而 Y∈R∣V∣×dY∈?^{|V|×d}Y∈R∣V∣×d 為包含d維嵌入的矩陣。矩陣的每一行對應一個節點的嵌入表示。此外,嵌入矩陣的正則化項 λ\lambdaλ 用于確保問題即使在缺乏足夠數據的情況下仍然具有良好的數值解。
該方法使用的損失函數主要是為了提高 GF 的性能和可擴展性。需要注意的是,該方法生成的解可能是噪聲。此外,通過查看其矩陣分解公式,我們可以觀察到 GF 執行的是強對稱分解。該特性特別適合鄰接矩陣對稱的無向圖,但對于有向圖可能會成為潛在的限制。
接下來,使用 Python 和 GEM 庫實現 networkx 圖的節點嵌入。
(1) 使用 networkx 生成啞鈴圖 G 作為 GF 算法的輸入:
G = nx.barbell_graph(m1=10, m2=4)
(2) 調用 GraphFactorization 類生成二維 (d=2) 嵌入空間:
gf = GraphFactorization(d=2, data_set=None,max_iter=10000, eta=1*10**-4, regu=1.0)
(3) 通過 gf.learn_embedding(G) 計算輸入圖的節點嵌入:
gf.learn_embedding(G)
(4) 使用 gf.get_embedding() 方法獲取計算得到的嵌入結果:
import matplotlib.pyplot as pltfig, ax = plt.subplots(figsize=(10,10))for x in G.nodes():v = gf.get_embedding()[x]ax.scatter(v[0],v[1], s=1000)ax.annotate(str(x), (v[0],v[1]), fontsize=12)
運行結果如下所示:

從圖中可以觀察到,屬于組 1 和組 3 的節點被映射到空間的同一區域,這些節點與組2的節點形成了明顯分隔。這種映射方式雖然能有效區分組1、組 3 與組 2,但未能實現組 1 與組 3 之間的清晰分離。
2.2 高階鄰接保留嵌入
高階鄰接保留嵌入 (higher-order proximity preserved embedding, HOPE) 是另一種基于矩陣分解原理的圖嵌入技術。該方法能夠保留高階鄰接信息,并且不強制其嵌入具有任何對稱性質。在具體描述方法前,我們需要明確一階鄰接和高階鄰接:
- 一階鄰接 (
first-order proximity):給定圖 G=(V,E)G=(V,E)G=(V,E),其中每條邊有一個權重 wijw_{ij}wij?,若節點對 (vi,vj)(v_i,v_j)(vi?,vj?) 之間存在邊,則說它們之間的一階鄰接度為邊權重 wijw_{ij}wij?,否則,兩節點之間的一階鄰接度為0 - 二階和高階鄰接 (
second- and high-order proximity):通過二階鄰接,我們可以捕捉每對節點之間的二階關系。對于任意頂點對 (vi,vj)(v_i,v_j)(vi?,vj?),二階鄰接可視為從 viv_ivi? 到 vjv_jvj? 的兩步轉移過程。高階鄰接則對這一概念進行了推廣,使得我們可以捕捉到更為全局的結構。因此,高階鄰接可理解為從 viv_ivi? 到 vjv_jvj? 的 kkk (k≥3k≥3k≥3) 步轉移關系
給定了鄰接的定義后,我們可以描述 HOPE 方法。形式上,設 G=(V,E)G=(V,E)G=(V,E) 為需要計算嵌入的圖,A∈R∣V∣×∣V∣A∈R^{|V|×|V|}A∈R∣V∣×∣V∣ 為其鄰接矩陣。該問題使用的損失函數 LLL 定義如下:
L=∣∣S?YS×YtT∣∣F2L=||S-Y_S\times Y_t^T||_F^2 L=∣∣S?YS?×YtT?∣∣F2?
其中,S∈R∣V∣×∣V∣S\in \mathbb R^{|V|\times |V|}S∈R∣V∣×∣V∣ 是從圖 GGG 生成的相似度矩陣,YS∈R∣V∣×dY_S\in \mathbb R^{|V|\times d}YS?∈R∣V∣×d 和 Yt∈R∣V∣×dY_t\in \mathbb R^{|V|\times d}Yt?∈R∣V∣×d 是兩個嵌入矩陣,表示 ddd 維嵌入空間。更詳細地說,YSY_SYS? 代表源嵌入,YtY_tYt? 代表目標嵌入。
HOPE 使用這兩個矩陣來捕捉有向網絡中的非對稱鄰接關系,有向網絡中存在從源節點到目標節點的方向性。最終的嵌入矩陣 YYY 通過將 YSY_SYS? 和 YtY_tYt? 矩陣按列簡單拼接而成。由于此操作,HOPE 生成的最終嵌入空間將具有 2?d2*d2?d 個維度。
如前所述,矩陣 SSS 是從原圖 GGG 獲得的相似度矩陣,其目的是獲取高階鄰接信息。SSS 被計算為 S=Mg?MlS = M_g \cdot M_lS=Mg??Ml?,其中 MgM_gMg? 和 MlM_lMl? 都是矩陣多項式。
HOPE 的作者提出了多種計算 MgM_gMg? 和 MlM_lMl? 的方法。本節,我們展示一種常見且簡便的計算方法——Adamic-Adar (AA)。在該方法中,Mg=IM_g = IMg?=I (單位矩陣),而 Ml=A?D?AM_l = A\cdot D\cdot AMl?=A?D?A,其中 DDD 是對角矩陣,其元素 Dij=1/(∑j(Aij+Aji))D_{ij} = 1/(∑_j(A_{ij}+A_{ji}))Dij?=1/(∑j?(Aij?+Aji?))。其他計算 MgM_gMg? 和 MlM_lMl? 的方法還包括 Katz 指數、Rooted PageRank (RPR) 和共同鄰居 (Common Neighbors, CN)。
接下來,使用 Python 和 GEM 庫對給定的 networkx 圖執行節點嵌入:
import networkx as nx
from gem.embedding.hope import HOPEG = nx.barbell_graph(m1=10, m2=4)hp = HOPE(d=4, beta=0.01)
hp.learn_embedding(G)
上述代碼與 GF 方法使用的代碼類似,唯一區別在于類初始化時需要指定使用 HOPE 算法。根據 GEM 提供的實現,參數 ddd (表示嵌入空間的維度)將決定最終嵌入矩陣 YYY 的列數——該矩陣由 YSY_SYS? 和 YtY_tYt? 經列向拼接而成。
因此,YSY_SYS? 和 YtY_tYt? 的實際列數由參數 ddd 的值通過取整除法確定。代碼運行結果如下所示:

在本節中,由于是無向圖,源節點與目標節點不存在差異。上圖展示了表示 YSY_SYS? 的嵌入矩陣前兩個維度的分布情況。可以看到,HOPE 生成的嵌入空間在這種情況下能夠更好地區分不同的節點。
2.3 帶有全局結構信息的圖表示
帶有全局結構信息的圖表示 (GraphRep),如 HOPE,能夠保留高階鄰接信息的同時,不強制嵌入具有對稱性。形式上,假設 G=(V,E)G=(V,E)G=(V,E) 是我們想要計算節點嵌入的圖,且 A=R∣V∣×∣V∣A=\mathbb R^{|V|\times |V|}A=R∣V∣×∣V∣ 是它的鄰接矩陣。該問題使用的損失函數 LLL 如下:
Lk=‖Xk?YSk×Ytk?‖F2L_k = ‖X^k - Y_S^k\times {Y_t^k}^?‖_F^2 Lk?=‖Xk?YSk?×Ytk??‖F2?
其中,Xk=R∣V∣×∣V∣X^k=\mathbb R^{|V|\times |V|}Xk=R∣V∣×∣V∣ 是為獲取節點間 kkk 階鄰接度而從圖 GGG 生成的矩陣,YSkY_S^kYSk? 和 Ytk∈R∣V∣×dY_t^k\in R^{|V|\times d}Ytk?∈R∣V∣×d 分別是表示源節點和目標節點 kkk 階鄰接度的 ddd 維嵌入矩陣。
XkX^kXk 矩陣通過以下公式計算:
Xk=Πk(D?1A)X^k = \Pi_k(D?1A) Xk=Πk?(D?1A)
其中 DDD 為度矩陣(對角矩陣),其元素:
Dij={∑pAipi=j0i≠jD_{ij}=\begin{cases} \sum_pA_{ip} & i=j \\ 0 & i \neq j \end{cases} Dij?={∑p?Aip?0?i=ji=j?
X1=D?1AX^1=D^{-1}AX1=D?1A 表示單步概率轉移矩陣,Xij1X_{ij}^1Xij1? 即節點 viv_ivi? 到 vjv_jvj? 的單步轉移概率。推廣至 kkk 階時,XijkX_{ij}^kXijk? 表示 kkk 步轉移概率。
對于每一階鄰接度 kkk,都會擬合一個獨立的優化問題。最終所有 kkk 個嵌入矩陣按列拼接,得到完整的源嵌入矩陣。
接下來,利用 Python 的 karateclub 庫實現 networkx 圖的節點嵌入:
import networkx as nx
from karateclub.node_embedding.neighbourhood.grarep import GraRepG = nx.barbell_graph(m1=10, m2=4)
gr = GraRep(dimensions=2,order=3)
gr.fit(G)
調用 karateclub 庫中的 GraRep 類進行初始化,dimension 參數表示嵌入空間的維度,而 order 參數定義節點之間鄰接度的最大階數。最終嵌入矩陣(存儲在 embeddings 變量中)的列數為 dimension * order,因為對于每一個鄰接度階數,都會計算一個嵌入并在最終嵌入矩陣中連接起來。
具體而言,本節中計算了兩個維度,因此 embeddings[:,:2] 表示 k=1k=1k=1 的嵌入,embeddings[:,2:4] 表示 k=2k=2k=2 的嵌入,embeddings[:,4:] 表示 k=3k=3k=3 嵌入。代碼運行結果如下所示:

從圖中可以看到,不同的鄰接階數會生成不同的嵌入分布。由于輸入圖結構較為簡單,當 k=1k=1k=1 時就已經獲得了良好分離的嵌入空間。具體而言,屬于組 1 和組 3 的節點在所有鄰接階數下都具有相同的嵌入值(在散點圖中呈現重疊狀態)。
本節我們介紹了幾種基于矩陣分解的無監督圖嵌入方法。下一節將探討使用 skip-gram 模型實現無監督圖嵌入的技術。
3. skip-gram 模型
skip-gram 在不同的嵌入算法應用廣泛,為了更好地理解這些方法,在深入詳細描述之前,我們首先進行簡要概述。
skip-gram 模型是一個簡單的神經網絡,具有一個隱藏層,其訓練目標是預測當輸入詞出現時特定詞匯共現的概率。神經網絡通過使用文本語料庫作為參考構建訓練數據進行訓練,具體流程如下所示:

上圖中所示的例子展示了算法如何生成訓練數據。首先選擇一個目標單詞,然后以其為中心構建固定窗口大小 w 的滑動窗口。窗口內的單詞稱為上下文單詞。然后,根據窗口中的單詞構建多組(目標單詞,上下文單詞)對。
當整個語料庫的訓練數據生成完畢后,skip-gram 模型便開始訓練,預測給定目標詞出現時各個詞匯作為上下文詞的概率。在訓練過程中,神經網絡學習輸入單詞的緊湊表示。這也就是 skip-gram 模型被稱為 Word2Vec 技術的原因。skip-gram 模型的結構如下所示:

神經網絡的輸入是一個大小為 m 的二元向量,其中每個元素對應待嵌入語言的詞典中的一個單詞。在訓練過程中,當輸入 (目標詞, 上下文詞) 詞對時,向量中僅有目標詞對應的位置取值為 1,其余元素均為 0。隱藏層有 d 個神經元,隱藏層將學習每個單詞的嵌入表示,創建一個 d 維的嵌入空間。
輸出層為包含 m 個神經元的全連接層(與輸入向量維度相同),采用 softmax 激活函數。每個神經元對應詞典中的一個單詞,其輸出值表示該詞與輸入目標詞的關聯概率。考慮到 m 值較大時 softmax 計算復雜度較高,實際應用中通常采用分層 softmax (hierarchical softmax) 方法。
需要強調的是,skip-gram 模型的最終目標并非完成上述預測任務,而是構建輸入單詞的 d 維緊湊向量表示。利用隱藏層的權重矩陣,即可方便地提取出詞匯的嵌入。另一種常見的 skip-gram 模型的變體是基于上下文預測目標詞,即連續袋詞模型 (Continuous Bag-of-Words, CBOW)。
在理解 skip-gram 模型基本原理后,我們繼續介紹基于該模型構建的無監督圖嵌入算法。這類算法的核心思想可概括為:首先從輸入圖中提取節點游走序列,將這些序列視為特殊"語料庫"——其中每個節點對應一個"詞匯",若兩個節點在游走序列中相鄰則視為"上下文鄰近"。不同算法的核心差異在于游走序列的生成策略,不同的游走生成算法能夠突出圖的特定局部或全局結構特征。
3.1 DeepWalk
DeepWalk 算法使用 skip-gram 模型生成給定圖的節點嵌入。為深入理解該模型,需要首先引入隨機游走 (random walk) 的概念。
設 GGG 為給定圖結構,選擇頂點 viv_ivi? 作為起點。隨機選擇 viv_ivi? 的一個鄰居節點并移動至該節點,再從新位置隨機選擇下一個移動節點,重復此過程 ttt 次。如此產生的 ttt 個頂點隨機序列即為長度為 ttt 的隨機游走。需特別說明的是,該游走生成算法未施加任何構建約束,因此不能保證節點的局部鄰域特征得到完整保留。
利用隨機游走的概念,DeepWalk 算法為每個節點生成一個最大長度為 ttt 的隨機游走。這些序列將作為 skip-gram 模型的輸入數據,使用 skip-gram 生成的嵌入將作為最終的節點嵌入。下圖展示了該算法的逐步執行過程:

上圖所示算法流程如下:
- 隨機游走生成:對于輸入圖 GGG 中的每個節點,生成 γγγ 條最大長度為 ttt 的隨機游走序列。需要注意的是,參數 ttt 僅為長度上限,不同路徑允許存在長度差異,并沒有約束要求所有路徑長度相同
skip-gram訓練:使用上一步中生成的所有隨機游走,訓練skip-gram模型。當圖作為輸入傳遞給skip-gram模型時,圖可以看作是輸入文本語料庫,而圖中的單個節點可以看作是語料庫中的一個單詞。隨機游走序列可以看作是一個單詞序列(句子)。然后,使用隨機游走中節點生成的“虛擬”句子訓練skip-gram模型。此步驟使用標準skip-gram模型參數,窗口大小w和嵌入大小d- 嵌入生成:從訓練完成的
skip-gram模型隱藏層中提取節點嵌入表示
接下來,使用 Python 和 karateclub 庫對給定的 networkx 圖執行節點嵌入:
dw = DeepWalk(dimensions=2)
從 karateclub 庫導入 DeepWalk 類進行初始化,dimensions 參數表示嵌入空間的維度。DeepWalk 類接受的其他參數包括:
walk_number:為每個節點生成的隨機游走數walk_length:生成的隨機游走的最大長度window_size:skip-gram模型的窗口大小
使用 dw.fit(G) 在圖 GGG 上擬合模型,并通過 dw.get_embedding() 提取嵌入:
dw.fit(G)
代碼執行結果如下所示:

從上圖中可以看到,DeepWalk 能夠將區域 1 與區域 3 分離開來。這兩個群體受到了屬于區域 2 的節點的干擾。實際上,在嵌入空間中,這些節點并沒有呈現出清晰的區分。
3.2 Node2Vec
Node2Vec 算法可以看作 DeepWalk 的擴展。DeepWalk 類似,Node2Vec 同樣通過生成隨機游走序列作為 skip-gram 模型的輸入。訓練完成后,skip-gram 模型的隱藏層將用于生成圖中節點的嵌入表示。兩種算法的核心差異在于隨機游走序列的生成方式。
具體而言,DeepWalk 采用無偏隨機游走,而 Node2Vec 引入了一種新技術,用于在圖中生成有偏隨機游走。該算法通過結合廣度優先搜索 (Breadth- First Search, BFS) 和深度優先搜索 (Depth-First Search, DFS) 的圖探索策略來生成游走序列。這兩種策略在游走生成中的組合比例由參數 ppp 和 qqq 調控——參數 ppp 控制隨機游走返回上一節點的概率,而參數 qqq 則調控游走探索圖中未訪問區域的可能性。
得益于這種組合機制,Node2Vec 既能保持圖中局部結構的高階鄰接關系,又能保留全局社群結構特征。這種隨機游走生成方法克服了 DeepWalk 在保持節點局部鄰域特性方面的局限性。
接下來,使用 Python 的 node2vec 庫實現 networkx 圖的節點嵌入:
node2vec = Node2Vec(G, dimensions=2)
model = node2vec.fit(window=10)
embeddings = model.wv
首先從 node2vec 庫中初始化 Node2Vec 類,dimensions 參數表示嵌入空間的維度。使用 node2vec.fit(window=10) 擬合模型。最后,使用 model.wv 獲取嵌入向量。
需要注意的是,model.wv 是 Word2VecKeyedVectors 類的對象。為了獲取特定節點的嵌入向量,假設 nodeid 是節點的 ID,我們可以使用訓練好的模型:model.wv[str(nodeId)]。此外,Node2Vec類還接受以下參數:
num_walks:為每個節點生成的隨機游走的數量walk_length:生成的隨機游走的長度p,q:隨機游走生成算法的 ppp 和 qqq 參數
代碼運行結果如下所示:

從上圖中可以看出,與 DeepWalk 相比,Node2Vec 能夠在嵌入空間實現更好的節點分離效果。具體而言,區域 1 和區域 3 的節點能很好地聚類在空間的兩個不同區域,而區域 2 的節點則恰當地分布在兩個群體之間,且沒有任何重疊。
3.3 Edge2Vec
Edge2Vec 算法生成的是邊的嵌入空間而非節點嵌入。該算法本質上是 Node2Vec 生成嵌入的一個簡單應用。其主要思想是使用兩個相鄰節點的節點嵌入進行一些基本的數學運算,以提取它們之間邊的嵌入表示。
設 viv_ivi? 和 vjv_jvj? 為兩個相鄰節點,f(vi)f(v_i)f(vi?) 和 f(vj)f(v_j)f(vj?) 分別表示通過 Node2Vec 計算得到的節點嵌入。下表中列出的運算符可用于計算它們之間連邊的嵌入表示:
| 運算符 | 公式 | 類名 |
|---|---|---|
| Average | f(vi)+f(vj)2\frac {f(v_i)+f(v_j)} 22f(vi?)+f(vj?)? | AverageEmbedder |
| Hadamard | f(vi)?f(vj)f(v_i)*f(v_j)f(vi?)?f(vj?) | HadamardEmbedder |
| Weighted-L1 | ∣f(vi)?f(vj)∣\lvert f(v_i)-f(v_j)\rvert∣f(vi?)?f(vj?)∣ | WeightedL1Embedder |
| Weighted-L2 | ∣f(vi)?f(vj)∣2\lvert f(v_i)-f(v_j)\rvert ^2∣f(vi?)?f(vj?)∣2 | WeightedL2Embedder |
接下來,使用 Python 和 Node2Vec 庫實現給定 networkx 圖的邊嵌入:
from node2vec.edges import HadamardEmbedder
embedding = HadamardEmbedder(keyed_vectors=model.wv)
用 keyed_vectors 參數實例化 HadamardEmbedder 類,參數的值是由 Node2Vec 生成的嵌入。為了使用其他技術生成邊嵌入,只需更換使用上表所列的其他算子類。嵌入結果如下所示:

3.4 Graph2Vec
前文所述方法都是針對給定圖中單個節點或邊生成嵌入空間,Graph2Vec 將這一概念進行泛化,能夠為整張圖生成嵌入表示。
具體來說,給定一組圖結構數據,Graph2Vec 算法生成一個嵌入空間,其中每個點代表一個圖。該算法使用 Word2Vec skip-gram 模型的變體,即 Document to Vector (Doc2Vec) 來生成嵌入表示。下圖展示了該模型的簡化示意圖:
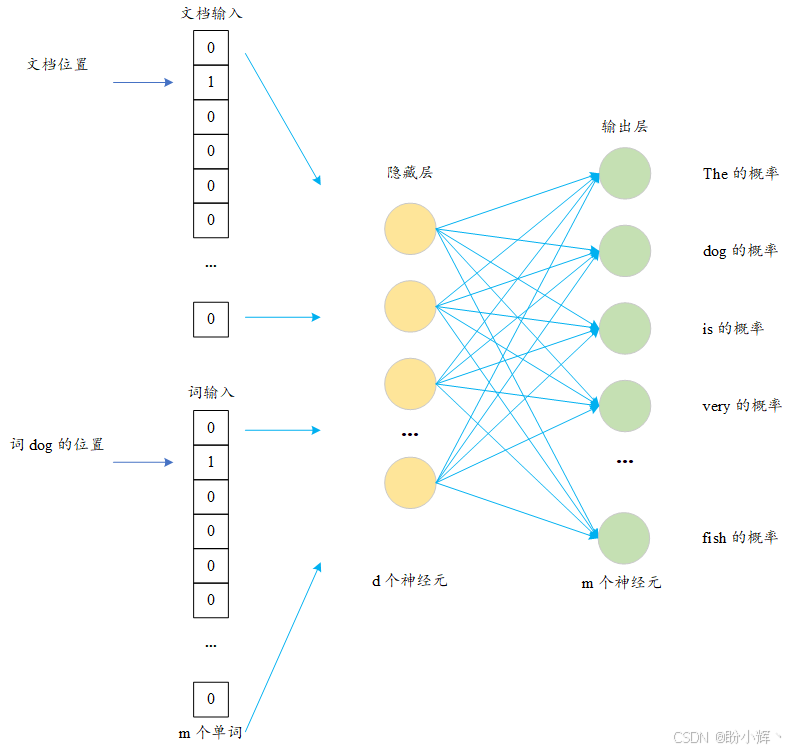
與簡單的 Word2Vec 相比,Doc2Vec 模型額外接收一個代表文檔的二元數組作為輸入。給定"目標"文檔和"目標"詞語,該模型會基于輸入的"目標"詞語及其所屬文檔,預測最可能出現的"上下文"詞語。
基于 Doc2Vec 模型,我們可以闡述 Graph2Vec 算法的核心思想:該方法將整張圖視為一個文檔,而將每個節點生成的自我圖 (ego graph) 視為構成該文檔的詞語。
換句話說,圖由子圖組成,正如文檔由句子組成。根據這一描述,算法可以總結為以下幾個步驟:
- 子圖生成:為每個節點生成一組帶根節點的子圖
Doc2Vec訓練:使用上一步驟生成的子圖來訓練Doc2Vec skip-gram模型- 嵌入生成:使用訓練好的
Doc2Vec模型的隱藏層中包含的信息來提取每個節點的嵌入
接下來,使用 Python 和 karateclub 庫實現一組 networkx 圖的圖嵌入。
(1) 使用隨機參數生成了 20 個 Watts-Strogatz 圖:
import random
import matplotlib.pyplot as plt
from karateclub import Graph2Vecn_graphs = 20def generate_radom():n = random.randint(6, 20)k = random.randint(5, n)p = random.uniform(0, 1)return nx.watts_strogatz_graph(n,k,p), [n,k,p]Gs = [generate_radom() for x in range(n_graphs)]
(2) 使用 karateclub 庫初始化 Graph2Vec 類,設置嵌入空間維度為 2:
model = Graph2Vec(dimensions=2, wl_iterations=10)
(3) 通過 model.fit(Gs) 方法在輸入數據上訓練模型:
model.fit([x[0] for x in Gs])
(4) 使用 model.get_embedding() 提取包含嵌入向量的數組:
embeddings = model.get_embedding()fig, ax = plt.subplots(figsize=(10,10))for i,vec in enumerate(embeddings):ax.scatter(vec[0],vec[1], s=1000)ax.annotate(str(i), (vec[0],vec[1]), fontsize=40)
代碼運行結果如下所示:
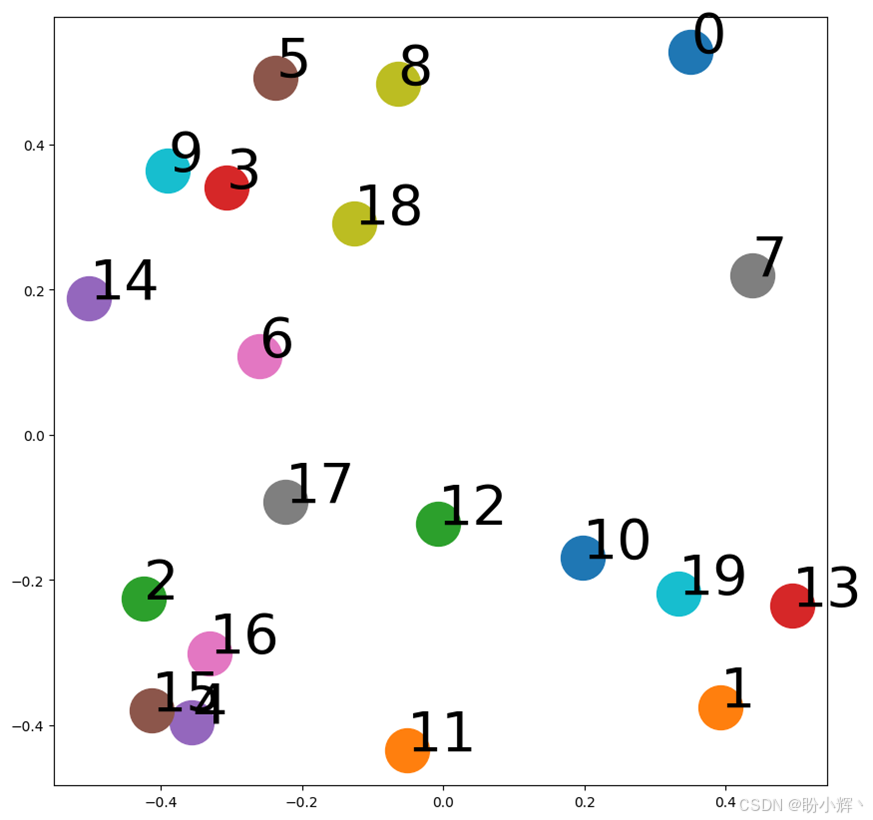
從上圖中可以看到為不同圖生成的嵌入。
在本節中,我們介紹了基于矩陣分解和 skip-gram 模型的多種淺層嵌入方法。




)


)
)


)
】MyBatis XML 注入審計)






