目錄

1.課題概述

2.系統仿真結果

3.核心程序

4.系統仿真參數

5.系統原理簡介

6.參考文獻

7.完整工程文件

---

1.課題概述

? ? ? ?基于Master-Slave主從博弈論的儲能與能源協調算法matlab仿真.主從博弈（Stackelberg Game）是一種具有層級決策結構的博弈模型，包含主導者（Leader）和跟隨者（Follower）兩類主體。在儲能與能源協調場景中，微網運營商（MGO）作為主導者，率先制定電價、熱價等策略；用戶聚合商（用戶側）作為跟隨者，根據主導者策略動態調整自身的用電、用熱及儲能使用策略，最終通過反向歸納法求解雙方策略的均衡點，實現系統整體效益最大化。

2.系統仿真結果

3.核心程序

matlab2024b

.................................
figure
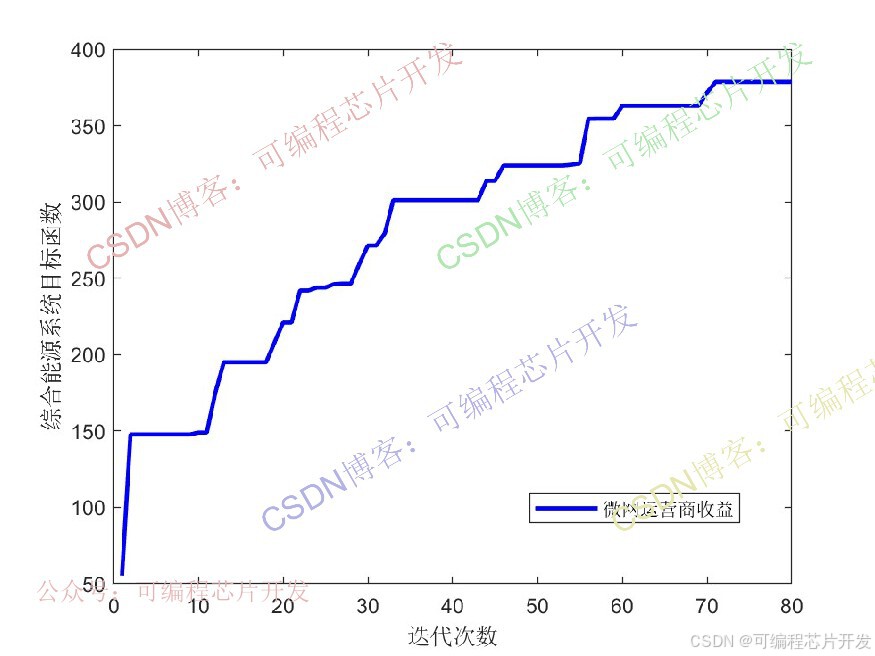
plot(yy1,'b','linewidth',2)
hold on
xlabel('迭代次數');
ylabel('綜合能源系統目標函數');
legend('微網運營商收益')xx=1:Tm;
PP=value([H_buy;Prl]);
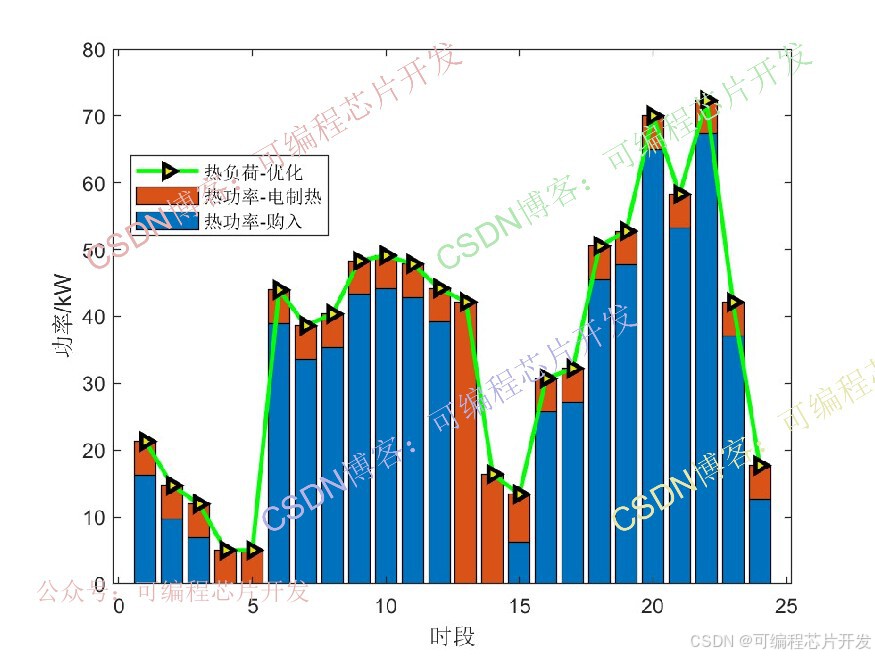
figure
bar(PP',0.8,'stack');
hold on
plot(value(H_buy+Prl),'-g>',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);legend('熱功率-購入','熱功率-電制熱','熱負荷-優化');
xlabel('時段');
ylabel('功率/kW');figure
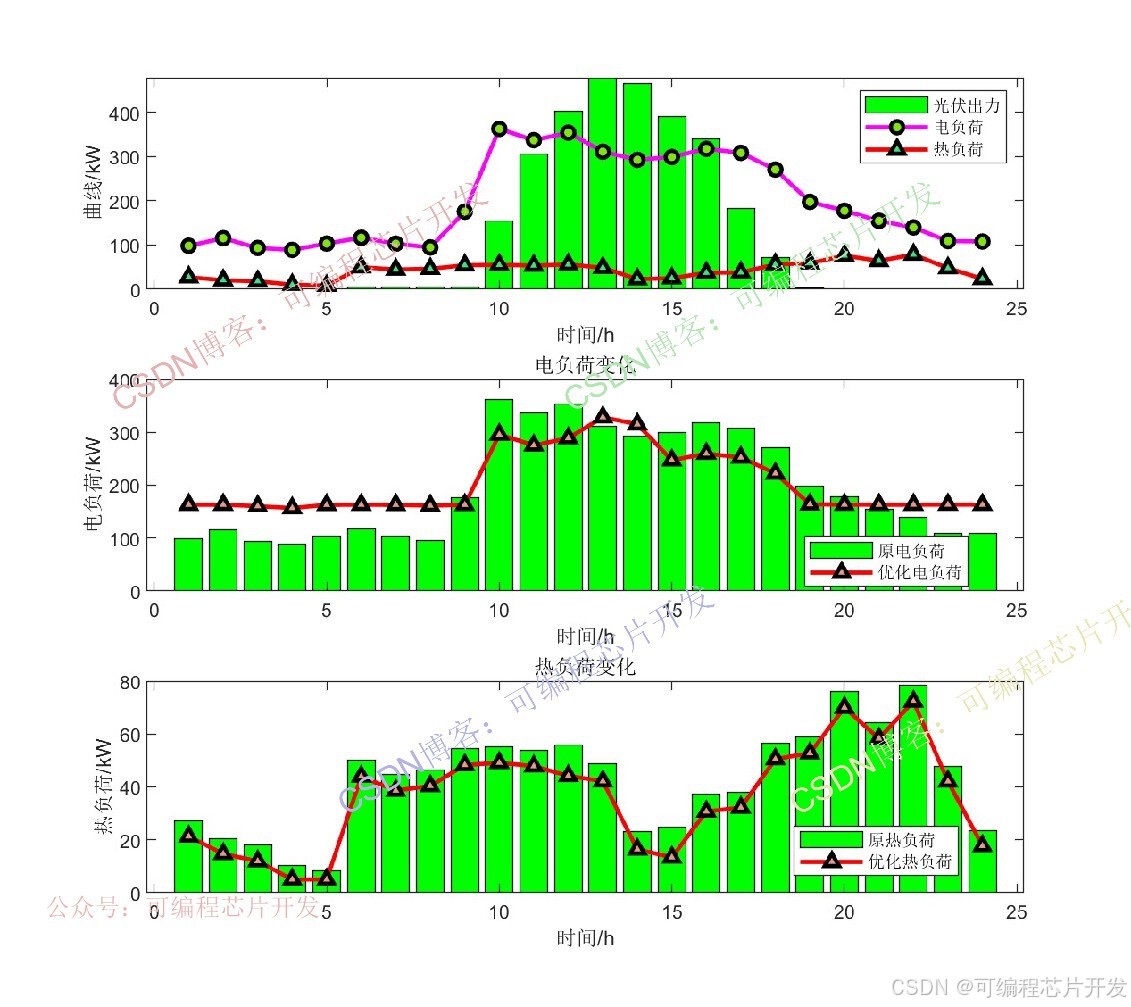
subplot(311);
bar(PV_pw,'g')
hold on
plot(E_load,'-mo',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.5,0.9,0.0]);hold on
plot(H_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.2,0.9,0.5]);hold on
xlabel('時間/h');
ylabel('曲線/kW');
legend('光伏出力','電負荷','熱負荷');subplot(312);
bar(E_load,'g');
hold on
plot(Eall_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.6,0.5]);hold on 
xlabel('時間/h');
ylabel('電負荷/kW');
title('電負荷變化');
legend('原電負荷','優化電負荷');subplot(313);
bar(H_load,'g');
hold on
plot(Hall_load,'-r^',...'LineWidth',2,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.6,0.5]);
hold on 
xlabel('時間/h');
ylabel('熱負荷/kW');
title('熱負荷變化');
legend('原熱負荷','優化熱負荷');figure
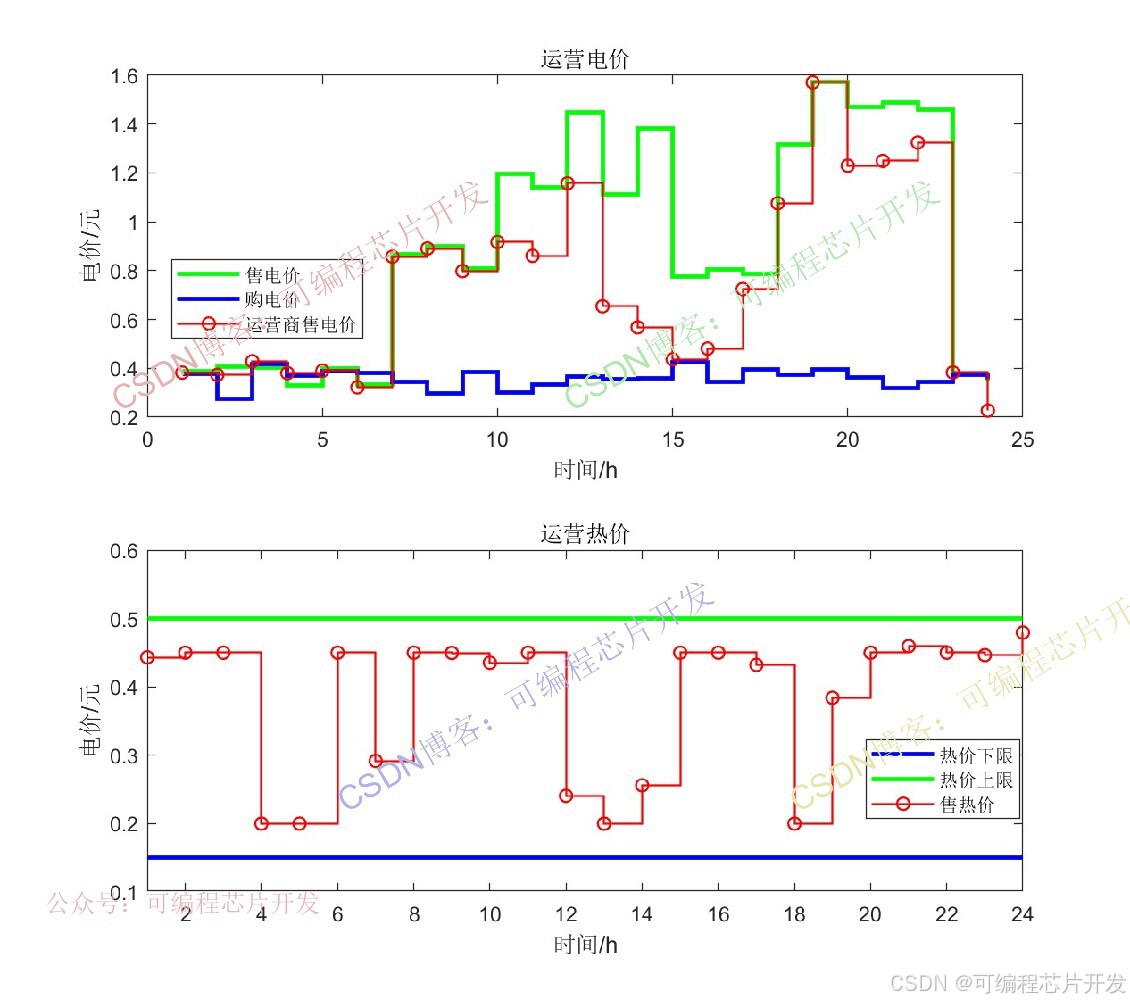
subplot(211);
xx=1:Tm;
stairs(Prices,'g','linewidth',2);
hold on
stairs(Priceb,'b','linewidth',2);
hold on
stairs(ybest(1,xx),'r-o','linewidth',1);
xlabel('時間/h');
ylabel('電價/元');
title('運營電價');
legend('售電價','購電價','運營商售電價');subplot(212);
xx=1:Tm;
stairs(Hmin,'b','linewidth',2);
hold on
stairs(Hmax,'g','linewidth',2);
hold on
stairs(ybest(1,xx+Tm),'r-o','linewidth',1);
xlabel('時間/h');
ylabel('電價/元');
title('運營熱價');
axis([1,Tm,0.1,0.6]);
legend('熱價下限','熱價上限','售熱價');
114

4.系統仿真參數

%主從博弈優化過程
%差分進化算法參數初始化
Pr   = 0.5;           % 變異縮放因子 
Pc   = 0.9;           % 交叉概率 %種群參數設置
Nums = 25;    % 種群規模 
dims = 48;    % 個體維度（前24維為電價，后24維為熱價）
Iters= 80;   % 最大迭代次數（控制算法運行周期）

5.系統原理簡介

決策目標：最大化自身收益，包含與電網的電力交易收益、向用戶售電售熱收益，同時最小化燃氣輪機運行成本。

微網運營商側：

用戶聚合商側：

將用戶聚合商的最優反應策略代入微網運營商模型，求解其收益最大化問題：

目標函數：最大化微網運營商收益

通過遺傳算法更新電價與熱價策略，具體操作包括：

選擇：基于輪盤賭選擇策略，保留高收益策略。

交叉：以交叉概率（如 80%）生成新策略組合。

變異：以變異概率（如 5%）隨機調整策略參數。

? ? ? ?該算法通過主從博弈框架實現了微網運營商與用戶聚合商的策略協同，結合共享儲能與電制熱等靈活資源，有效提升了系統整體效益。未來可擴展方向包括：

多主體博弈：引入共享儲能運營商作為獨立博弈方，優化其服務費定價策略；

不確定性建模：考慮光伏出力、負荷需求的隨機性，采用隨機規劃或魯棒優化；

實時調度：結合模型預測控制（MPC），將日前優化擴展至日內滾動優化。

6.參考文獻

[1] 董朝陽，趙俊華，文福拴，等。從智能電網到能源互聯網：基本概念與研究框架 [J]. 電力系統自動化，2014,38 (15):1-11.
[2] 孫宏斌，郭慶來，潘昭光。能源互聯網：理念、架構與前沿展望 [J]. 電力系統自動化，2015,39 (19):1-8.
[3] 丁濤，牟晨璐，別朝紅，等。能源互聯網及其優化運行研究現狀綜述 [J]. 中國電機工程學報，2018,38 (15):4318-4328+4632.
[4]MOHSENIAN-RAD H. Coordinated price-maker operation of large energy storage units in nodal energy markets[J]. IEEE Trans on Power Systems,2016,31(1):786-797.

7.完整工程文件

v

v