1 3D到2D透視投影

? ? 三維空間上點? p 投影到二維空間 q 有兩種方式：1）正交投影，2）透視投影。

? ? 正交投影直接舍去 z 軸信息，該模型僅在遠心鏡頭上是合理的，或者對于物體深度遠小于其到攝像機距離時的近似模型。

? ? 常規鏡頭成像可以使用透視投影建模，如下圖：

? ? ??

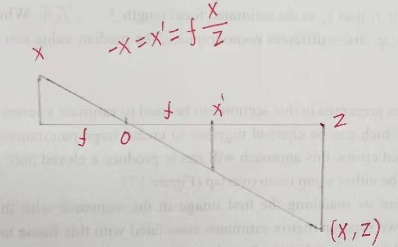
? ? 三維空間點 p=(X,Y,Z) 投影到二維空間點 q = (x,y)，鏡頭光軸在 Z 軸上，滿足關系?

，

? ? 真實的物理模型將 X 投影到 x, 但使用?

?可以避免關系式中產生一個負號，因此投影點可寫為?

,?同理，有?

。

? ? 使用矩陣可表示為?

，變換結果?

?為齊次坐標，

。

? ? 以上變換舉證前三列可表達相機自身相關性質，被稱為內參，比如?

，其中， f 表示相機焦距，af表示像元橫縱比（一般情形下為 1），

? ? cx,cy 表示 CCD 中心與光軸間平移距離，s 表示了 CCD 法向量與光軸不平行程度。

? ? 在實際應用中，一般會使用簡單模型?

，該模型僅表達了焦距與CCD中心平移。

? ? 如果將以上變換矩陣改寫成滿秩矩陣，那么其逆變換就變得很簡單，使用 4*4 變換矩陣重新構造透視投影如下：

? ? ?

，

，

,

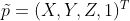
? ? 改寫齊次坐標?

，前兩個分量表示圖像上坐標值，第四個分量表示深度信息。

? ? 以上透視投影模型要求三維空間坐標滿足以下條件：

? ? 1）以鏡頭光心（小孔成像中的小孔）為原點；

? ? 2）Z軸垂直與 CCD 平面；

? ? 3）XY軸與 CCD 平面 xy 軸平行；

? ? 但在實際三維坐標系可能是任意建立的，所以在透視投影前需要變換坐標系，使用平移+旋轉模型如下：

? ??

，其中，R 為 3*3 旋轉矩陣，t 為平移向量。

? ? 綜上，任意三維空間上點到二維平面的透視投影可表示為?

，

，

。

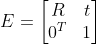
2 成對圖像配準

? ? ? ?

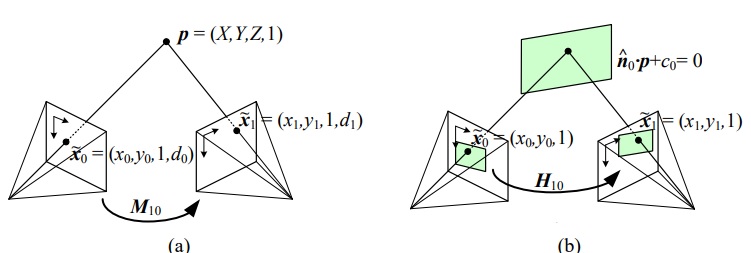
? ? 如上圖(a)所示，三維空間上點 p 映射到圖像平面為?

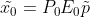
，由于?

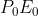
?均為滿足矩陣，故其逆矩陣一定存在，有?

。

? ? 結合?

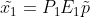
?可建立?

?與?

?之間的關系為?

。

? ? 以上關系需要相機記錄成像點深度信息，一般相機無法記錄深度信息，因此，可以使用圖像 (b)建立關系：

? ? 假設所有三維空間上點均在一個空間平面上，即滿足?

，

? ? 當進行投影變換時，其深度信息為零, 具體可表達為??

，

? ? 觀察可知，刪除變換矩陣最后一行與最后一列不影響計算結果，因此，可簡化表達式為?

，

? ? 以上變換有 8 個自由度，將變換矩陣重新改寫為?

，

? ? 變換矩陣?

?表達了平面場景的映射關系，這正好是 “圖像配準” 一文中使用的模型之一。

3 旋轉全景模型

? ? 在一個固定的世界坐標下，假設相機繞某旋轉點旋轉拍照，兩次（或多次）拍照間相機坐標原點保持不變，但光軸隨旋轉發生改變。

? ? 三維空間中任意固定點在每次拍照中的映射可表達為：

? ? 1）建立相機坐標系（原點與世界坐標系一致，光軸為相機當前光軸）；

? ? 2）使用旋轉矩陣 R 將世界坐標系下點旋轉為相機坐標系下點；

? ? 3）使用投影矩陣投影到相機平面；

? ? 因此，三維空間點在兩幅圖像中的映射關系可簡化為?

，

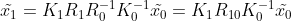
? ? 假設 K 僅包含相機焦距信息，則?

，

? ??

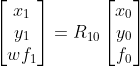
，當焦距已知時，此參數僅為旋轉，當焦距未知時，可以是固定焦距或者變化焦距。

? ? 一般情況下，該變化的參數個數為 4，包括 1）固定未知焦距，2）旋轉參數（3個），

? ? 這比8個參數投影變換更加簡化，該模型是用于全景圖像拼接的理想模型。

4 迭代求解

? ? 給定一對圖像上若干匹配點?

，使用平面投影變換可得?

，

? ? 兩邊同時乘以分母得?

，

? ? 進一步整理為?

，

? ? 使用該線性方程組可以求解變換矩陣?

?的初始估計。

? ? 在初始估計?

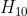
?基礎上使用非線性迭代方程為?

,

? ??

，

? ??

?為變換矩陣?

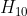
?的估計，

?為第二次迭代估計，通過最小化第二次估計誤差即求得合理的?

。

? ? 如果在每次迭代估計中使用上次迭代估計值?

?作為初始估計，即?

?中各個參數值均為零，迭代方程可改寫為

? ??

，

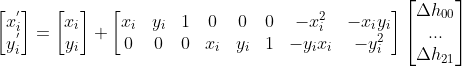
? ? 注意，以上?

?不再是初始匹配點，而是每次迭代后的計算點！！！

? ? 在旋轉全景模型中，

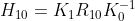
，當旋轉分量增加?

?后，

? ? 旋轉矩陣為??

,??

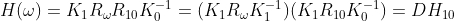
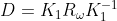
?為增量矩陣。

? ??

，當??

?為弧度單位且很小時，

，

? ??

，

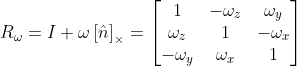
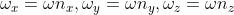
?表示旋轉軸。

? ? 增量矩陣 D 可改寫為?

，

? ? D 中變量為旋轉角度?

?，使用線性近似可表達為?

，

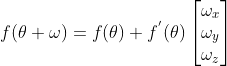
? ? 其中，

?為初始估計參數的變換結果，

?為旋轉一個小的角度?

?后的線性變換結果，

? ? 使用最小二乘法可以求解一個合理的旋轉角度。

? ? 觀察增量矩陣 D，可以發現 D 與 H 存在一種對應關系?

，

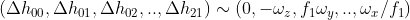
? ? 迭代公式?

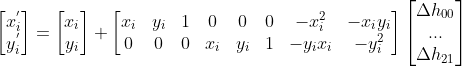
?可轉換為：

? ? ?

，

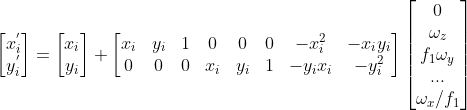
? ? 整理公式，使其為?

?的線性函數?

，

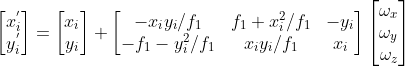
? ? 使用最小二乘法可以求解一個合理的旋轉角度。

? ? 以上迭代公式中，

?是一個未知量，但是可以從初始估計?

?中計算得出，具體如下：

? ??

，

? ?

，

? ??

，該旋轉矩陣為正交矩陣，

? ? 在旋轉矩陣每一項上乘以一個因子?

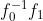
?不會改變矩陣正交特性，因此，可將上式改寫為：

? ??

，利用正交特性有：

? ??

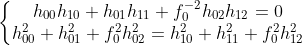
，可求解?

，

? ? 同理，利用第三行與第一行正交可求解?

，當焦距相等時，可估計焦距為

。?

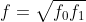
5 全局配準

? ? 由于每對圖像間的配準估計均可能存在誤差，當多幅圖像通過圖像對間配準參數配準時，會形成累積誤差，

? ? 這在全景圖像拼接中可能產生縫隙或者過疊加，所以需要校正圖像對間配準參數，稱作光束平差法(bundle adjustment)。

? ? 在光束平差法之前，通過圖像對間特征點匹配情況可以剔除一些孤立圖像，然后在保留圖像中進行全局配準。

? ? 假設有 n 幀圖像用于形成全景圖像，三維空間中有 m 個特征點在至少兩幀圖像中形成了映射關系，

? ??

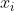
?表示第? i 個三維空間點，

?表示第 i 個三維空間點在第 j 幀圖像上形成的投影點，

?表示得 i 個三維空間點在第 j 幀圖像上是否存在投影點。

? ? 利用旋轉全景模型可建立?

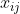
?到?

?的映射為?

，

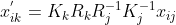
? ? 最小化?

?即可。

? ? 完成全局配準后，全景圖像仍然可能存在局部錯位，這可能是因為鏡頭鏡像畸變，攝像頭沒有完全繞光軸中心旋轉，場景中微小抖動等因素引起。

? ? 可以通過對整幅全景圖像建立一個類似稠密光流估計圖來抵消局部誤差，方法如下：

? ? 1）已經通過光束平差法重新估計了變換矩陣；

? ? 2）利用?

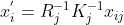
?計算第 j 幀圖像對應的第 i 個特征點位置；

? ? 3）求所有圖像幀上對應的第 i 個特征點的平均位置?

；

? ? 4）求第 i 個特征點在第 j 幀圖像上的精確位置?

；

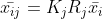
? ? 5）求第 i 個特征點在第 j 幀圖像上擾動?

;

? ? 6）使用插值構造全景圖像上局部擾動，用于全景拼接時補償局部模糊。

6 圖像合成

? ? 當所有相關圖像都完成注冊后，我們可以利用以上信息產生一張完整的拼接圖像，這個過程大致包括以下內容：

? ? 1）選擇合成表面，當少量圖像拼接時，可以選擇平坦全景圖；當全景圖視野很大時，如果選擇平坦全景圖，

? ? 則在周邊區域會產生很大扭曲變形，這時一般選擇圓柱面投影或者球面投影；

? ? 2）決定那一幀圖像作為中間參考圖像，由于已經知道每一幀圖像對應的旋轉角度，一般旋轉平均旋轉角度附近的圖像作為中間參考圖像；

? ? 3）將參考圖像平移到合成表面中心，將其他圖像按已知注冊信息映射到合成表面；

? ? 4）在重疊部分通過加權方式去除虛影；

? ? 5）使用拉普拉斯金字塔融合方案融合圖像，必要時進行曝光補償。