文章目錄
- 循環神經網絡(RNN)
- 簡單的循環神經網絡
- 長短期記憶網絡(LSTM)
- 門控循環單元(GRU)
循環神經網絡(RNN)
- 循環神經網絡(RecurrentNeuralNetwork,RNN)又稱遞歸神經網絡,它是常規前饋神經網絡(FeedforwardNeuralNetwork,FNN)的擴展,本節介紹幾種常見的循環神經網絡。
簡單的循環神經網絡
- 循環神經網絡(RNN)會遍歷所有序列的元素,每個當前層的輸出都與前面層的輸出有關,會將前面層的狀態信息保留下來。理論上,RNN應該可以處理任意長度的序列數據,但為了降低一定的復雜度,實踐中通常只會選取與前面的幾個狀態有關的信息。
- 簡單的循環神經網絡如圖:

- x是輸入,y是輸出,中間由一個箭頭表示數據循環更新的是隱藏層,主要由中間部分實現時間記憶功能。
- 神經網絡輸入x并產生輸出y,最后將輸出的結果反饋回去。假設在一個時間t內,神經網絡的輸入除來自輸入層的 x ( t ) x(t) x(t)外,還有上一時刻的輸出 y ( t ? 1 ) y(t-1) y(t?1),兩者共同輸入產生當前層的輸出 y ( t ) y(t) y(t)。
- 將這個神經網絡按照時間序列形式展開:

- 每個神經元的輸出都是根據當前的輸入 x ( t ) x(t) x(t)和上一時刻的 y ( t ? 1 ) y(t-1) y(t?1)共同決定。它們對應的權重分別是 W x W_x Wx?和 W y W_y Wy?,單個神經元的輸出計算如下:
y t = O ( x t T ? W x + y t ? 1 T ? W y + b ) \boldsymbol { y } _ { t } = \mathcal { O } ( \boldsymbol { x } _ { t } ^ { \mathrm { T } } \cdot \boldsymbol { W } _ { x } + \boldsymbol { y } _ { t - 1 } ^ { \mathrm { T } } \cdot \boldsymbol { W } _ { y } + b ) yt?=O(xtT??Wx?+yt?1T??Wy?+b) - 將隱藏層的層級展開,結果如下圖:
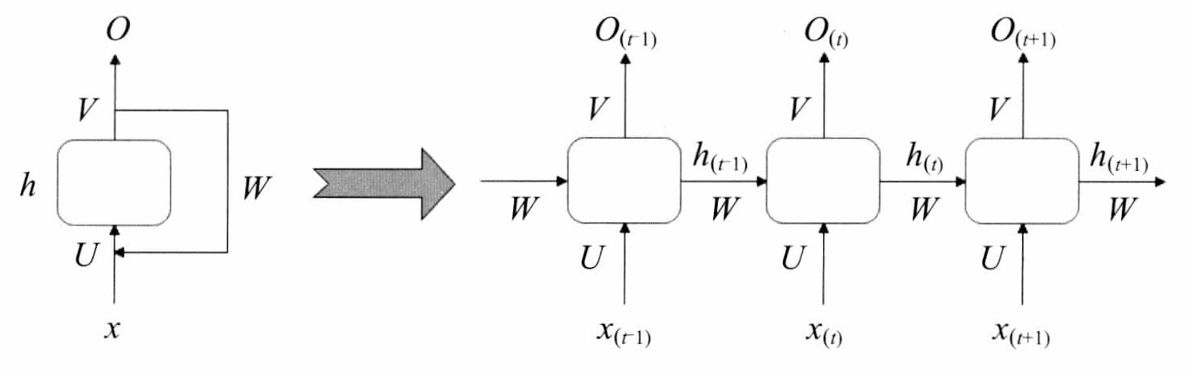
- RNN單元在時間 t t t的狀態記作 h t h_t ht?, U U U表示此刻輸入的權重, W W W表示前一次輸出的權重, V V V表示此刻輸出的權重。
- 在 t = 1 t=1 t=1時刻,一般 h 0 h_0 h0?表示初始狀態為0,隨機初始化 U 、 W 、 V U、W、V U、W、V,公式如下:
h 1 = f ( U x 1 + W h 0 + b h ) O 1 = g ( V h 1 + b o ) \begin {array} { l } { h _ { 1 } = f ( U x _ { 1 } + W h _ { 0 } + b _ { h } ) } \\ { O _ { 1 } = g ( V h _ { 1 } + b _ { o } ) } \\ \end{array} h1?=f(Ux1?+Wh0?+bh?)O1?=g(Vh1?+bo?)? - f 和 g 均為激活函數(光滑的曲線函數), f f f可以是Sigmoid、ReLU、Tanh等激活函數, g g g通常是Softmax損失函數。 b h b_h bh?是隱藏層的偏置項, b 0 b_0 b0?是輸出層的偏置項。
- 前向傳播算法,按照時間 t t t向前推進,而此時隱藏狀態 h 1 h_1 h1?是參與下一個時間的預測過程。
h 2 = f ( U x 2 + W h 1 + b h ) O 2 = g ( V h 2 + b o ) \begin {array} { l } { h _ { 2 } = f ( U x _ { 2 } + W h _ { 1 } + b _ { h } ) } \\ { O _ { 2 } = g ( V h _ { 2 } + b _ { o } ) } \\ \end{array} h2?=f(Ux2?+Wh1?+bh?)O2?=g(Vh2?+bo?)? - 以此類推,最終可得到輸出公式為:
h t = f ( U x t + W h t ? 1 + b h ) O t = g ( V h t + b o ) \begin {array} { l } { h _ { t } = f ( U x _ { t } + W h _ { t-1 } + b _ { h } ) } \\ { O _ { t } = g ( V h _ { t } + b _ { o } ) } \\ \end{array} ht?=f(Uxt?+Wht?1?+bh?)Ot?=g(Vht?+bo?)? - 權重共享機制通過統一網絡參數(W、U、V及偏置項)實現了三方面優勢:一是降低計算復雜度,二是增強模型泛化能力,三是實現對可變長度連續序列數據的特征提取。該機制不僅能捕捉序列特征的時空連續性,還通過位置無關的特性避免了逐位置規則學習,但保留了序列位置的識別能力。
- 盡管RNN網絡在時序數據處理上表現優異,其基礎結構仍存在顯著缺陷。理論上RNN應具備長期記憶能力和任意長度序列處理能力,但實際應用中會出現梯度消失現象。該問題源于兩方面:一是BP算法的固有缺陷(前饋神經網絡中隨深度增加出現訓練失效),二是RNN特有的長程依賴問題(時間跨度導致記憶衰減)。從數學視角看,當激活函數導數小于1時,多層網絡梯度呈指數衰減;反之若導數大于1則引發指數級梯度膨脹,造成網絡失穩(即梯度爆炸問題)。
- 針對這些局限性,學界提出了兩種主流改進架構:長短期記憶網絡(LSTM)和門控循環單元(GRU)。
長短期記憶網絡(LSTM)
- 長短期記憶網絡(Long Short-Term Memory,LSTM)主要為了解決標準RNN在處理長序列數據時面臨的梯度消失等問題。
- 基本的LSTM結構單元如圖:

- 圖中四個矩形即圖標1,2,3,4是普通神經網絡的隱藏層結構。其中 f ( t ) , i t , o ( t ) f_{(t),i_{{t}},o_(t)} f(t),it?,o(?t)?都是Logistic函數, g ( t ) g_{(t)} g(t)?是Tanh函數。
- LSTM單元狀態分為長時記憶和短時記憶,其中短時記憶i用向量 h ( t ) h_{(t)} h(t)?表示,長時記憶用 c ( t ) c_{(t)} c(t)?表示。
- LSTM單元結構中還有三個門限控制器:忘記門限,輸入門限和輸出門限。三個門限都使用Logistic函數,如果輸出值為1,表示門限打開;如果輸出值為0,表示門限關閉。
- 忘記門限:主要用 f ( t ) f_{(t)} f(t)?控制著長時記憶是否被遺忘。
- 輸入門限:主要由 i ( t ) i_{(t)} i(t)?和 g t g_{{t}} gt?, i ( t ) i_{(t)} i(t)?用于控制 g t g_{{t}} gt?用于增強記憶的部分。
- 輸出門限:主要由 o ( t ) o_{(t)} o(t)?控制應該在該時刻被讀取和輸出的部分。
- LSTM單元的基本流程如下:隨著短時記憶 c ( t ) c_{(t)} c(t)?從左到右橫穿整個網絡,它首先經過一個遺忘門,丟棄一些記憶,然后通過輸入門限來選擇增加一些新記憶,最后直接輸出 c ( t ) c_{(t)} c(t)?。此外,增加記憶這部分操作中,長時記憶先經過Tanh函數,然后被輸出門限過濾,產生了短時記憶ht)。
- 綜上所述,LSTM可以識別重要的輸入(輸入門限的作用),并將這些信息在長時記憶中存儲下來,通過遺忘門保留需要的部分,以及在需要的時候能夠提取它。
- LSTM單元結構中的三個門限控制器、兩種狀態以及輸出:
i ( t ) = σ ( w × i ? ? x ( t ) + w h i ? ? h ( t ? 1 ) + b i ) f ( t ) = σ ( w × j ? ? x ( t ) + w h j ? ? h ( t ? 1 ) + b f ) o ( t ) = σ ( w x o ? ? x ( t ) + w h o ? ? h ( t ? 1 ) + b o ) g ( t ) = T a n h ( w x g ? ? x ( t ) + w h g ? ? h ( t ? 1 ) + b g ) c ( t ) = f ( t ) ? c ( t ? 1 ) + i ( t ) ? g ( t ) y ( t ) = h ( t ) = o ( t ) ? T a n h ( c ( t ) ) \begin{array} { r l } & { i _ { ( t ) } = \sigma ( w _ { \times i } ^ { \top } \cdot x _ { ( t ) } + w _ { h i } ^ { \top } \cdot h _ { ( t - 1 ) } + b _ { i } ) } \\ & { f _ { ( t ) } = \sigma ( w _ { \times j } ^ { \top } \cdot x _ { ( t ) } + w _ { h j } ^ { \top } \cdot h _ { ( t - 1 ) } + b _ { f } ) } \\ & { o _ { ( t ) } = \sigma ( w _ { x o } ^ { \top } \cdot x _ { ( t ) } + w _ { h o } ^ { \top } \cdot h _ { ( t - 1 ) } + b _ { o } ) } \\ & { g _ { ( t ) } = \mathrm { T a n h } ( w _ { x g } ^ { \top } \cdot x _ { ( t ) } + w _ { h g } ^ { \top } \cdot h _ { ( t - 1 ) } + b _ { g } ) } \\ & { c _ { ( t ) } = f _ { ( t ) } \otimes c _ { ( t - 1 ) } + i _ { ( t ) } \otimes g _ { ( t ) } } \\ & { y _ { ( t ) } = h _ { ( t ) } = o _ { ( t ) } \otimes \mathrm { T a n h } ( c _ { ( t ) } ) } \end{array} ?i(t)?=σ(w×i???x(t)?+whi???h(t?1)?+bi?)f(t)?=σ(w×j???x(t)?+whj???h(t?1)?+bf?)o(t)?=σ(wxo???x(t)?+who???h(t?1)?+bo?)g(t)?=Tanh(wxg???x(t)?+whg???h(t?1)?+bg?)c(t)?=f(t)??c(t?1)?+i(t)??g(t)?y(t)?=h(t)?=o(t)??Tanh(c(t)?)? - w x i 、 w x f 、 w x o 、 w x g w_{xi}、w_{xf}、w_{xo}、w_{xg} wxi?、wxf?、wxo?、wxg?是每一層連接到 x ( t ) x_{(t)} x(t)?的權重, w h i 、 w h f 、 w h o 、 w h g w_{hi}、w_{hf}、w_{ho}、w_{hg} whi?、whf?、who?、whg?是每層連接到前一個短時記憶 h ( t ? 1 ) h_{(t-1)} h(t?1)?的權重, b i 、 b f 、 b o 、 b g b_i、b_f、b_o、b_g bi?、bf?、bo?、bg?是每一層的偏置項。
門控循環單元(GRU)
-
門控循環單元(GateRecurrentUnit,GRU)是循環神經網絡(RNN)的一個變種,它旨在解決標準RNN中梯度消失的問題。GRU結構更簡單,效果更好。
-
GRU的設計初衷是解決長期依賴問題,即標準RNN難以捕捉長序列中較早時間步的信息。通過引入更新門和重置門,GRU能夠學習到何時更新或忽略某些信息,從而更好地處理序列數據。
-
相較于LSTM,GRU有更少的參數和計算復雜度,特別是在資源受限的情況下訓練更快,同時也能取得不錯的性能表現,。GRU已被廣泛應用于各種序列建模任務,如語言模型、機器翻譯、語音識別等領域。
-
GRU如圖所示:

-
GRU中包含三個激活函數,分別為Logistic、Logistic、Tanh函數。
-
如圖所示,GRU通過精簡門控機制提升了計算效率,其核心特征如下:
-
門控結構簡化:
- 采用**重置門(r)和更新門(z)**雙門架構,激活函數縮減至3個(使用Sigmoid或Logistic函數,輸出0~1的門控信號)。
- 合并狀態向量為單一隱藏狀態 h t h_t ht?,簡化信息流動路徑。
-
門控功能詳解:
- 重置門(r):控制前一時刻隱藏狀態 h t ? 1 h_{t-1} ht?1?對當前候選狀態的影響程度。門值越接近0,丟棄的歷史信息越多,主層(如Tanh激活單元)將更多依賴當前輸入 x t x_t xt? 重新計算候選狀態。
- 更新門(z):調節 h t ? 1 h_{t-1} ht?1? 傳遞至當前狀態 h t h_t ht? 的比例。門值越接近1,保留的歷史信息比例越高,新生成的信息比例越低。
-
工作流程:
- 步驟1:根據 h t ? 1 h_{t-1} ht?1? 和 x t x_t xt? 計算重置門 r t r_t rt? 和更新門 z t z_t zt?。
- 步驟2:利用 r t r_t rt? 重置 h t ? 1 h_{t-1} ht?1?,生成候選狀態 h ~ t \tilde{h}_t h~t?(通常通過Tanh激活)。
- 步驟3:通過 z t z_t zt? 加權融合 h t ? 1 h_{t-1} ht?1? 與 h ~ t \tilde{h}_t h~t?,輸出最終狀態 h t h_t ht?。
- GRU單元結構的計算過程:
z ( t ) = σ ( w x z T ? x ( t ) + w h z T ? h ( t ? 1 ) ) r ( t ) = σ ( w x r T ? x ( t ) + w h r T ? h ( t ? 1 ) ) g ( t ) = T a n h ( w x g T ? x ( t ) + w h g T ? ( r ( t ) ? h ( t ? 1 ) ) ) h ( t ) = ( 1 ? z ( t ) ) ? T a n h ( w x g T ? h ( t ? 1 ) + z ( t ) ? g ( t ) ) \begin{array} { r l } & { z _ { ( t ) } = \sigma ( w _ { x z } ^ { \mathrm { T } } \cdot x _ { ( t ) } + w _ { h z } ^ { \mathrm { T } } \cdot h _ { ( t - 1 ) } ) } \\ & { r _ { ( t ) } = \sigma ( w _ { x r } ^ { \mathrm { T } } \cdot x _ { ( t ) } + w _ { h r } ^ { \mathrm { T } } \cdot h _ { ( t - 1 ) } ) } \\ & { g _ { ( t ) } = \mathrm { T a n h } ( w _ { x g } ^ { \mathrm { T } } \cdot x _ { ( t ) } + w _ { h g } ^ { \mathrm { T } } \cdot ( r _ { ( t ) } \otimes h _ { ( t - 1 ) } ) ) } \\ & { h _ { ( t ) } = ( 1 - z _ { ( t ) } ) \otimes \mathrm { T a n h } ( w _ { x g } ^ { \mathrm { T } } \cdot h _ { ( t - 1 ) } + z _ { ( t ) } \otimes g _ { ( t ) } ) } \end{array} ?z(t)?=σ(wxzT??x(t)?+whzT??h(t?1)?)r(t)?=σ(wxrT??x(t)?+whrT??h(t?1)?)g(t)?=Tanh(wxgT??x(t)?+whgT??(r(t)??h(t?1)?))h(t)?=(1?z(t)?)?Tanh(wxgT??h(t?1)?+z(t)??g(t)?)? - w x z 、 w x r w_{xz}、w_{xr} wxz?、wxr? 和 w x g w_{xg} wxg?是每一層連接到輸入 x ( t ) x(t) x(t)的權重, W h z 、 W h r , W_{hz}、W_{hr}, Whz?、Whr?,和 W h g W_{hg} Whg? 是每一層連接到前一個短時記憶 h ( t ? 1 ) h_{(t-1)} h(t?1)?的權重。






)
)


)


{ :|: };:)





