無人機避障——（運動規劃部分）深藍學院動力學kinodynamic A* 3D算法理論解讀（附C++代碼）

開源代碼鏈接：GitHub - Perishell/motion-planning

效果展示：

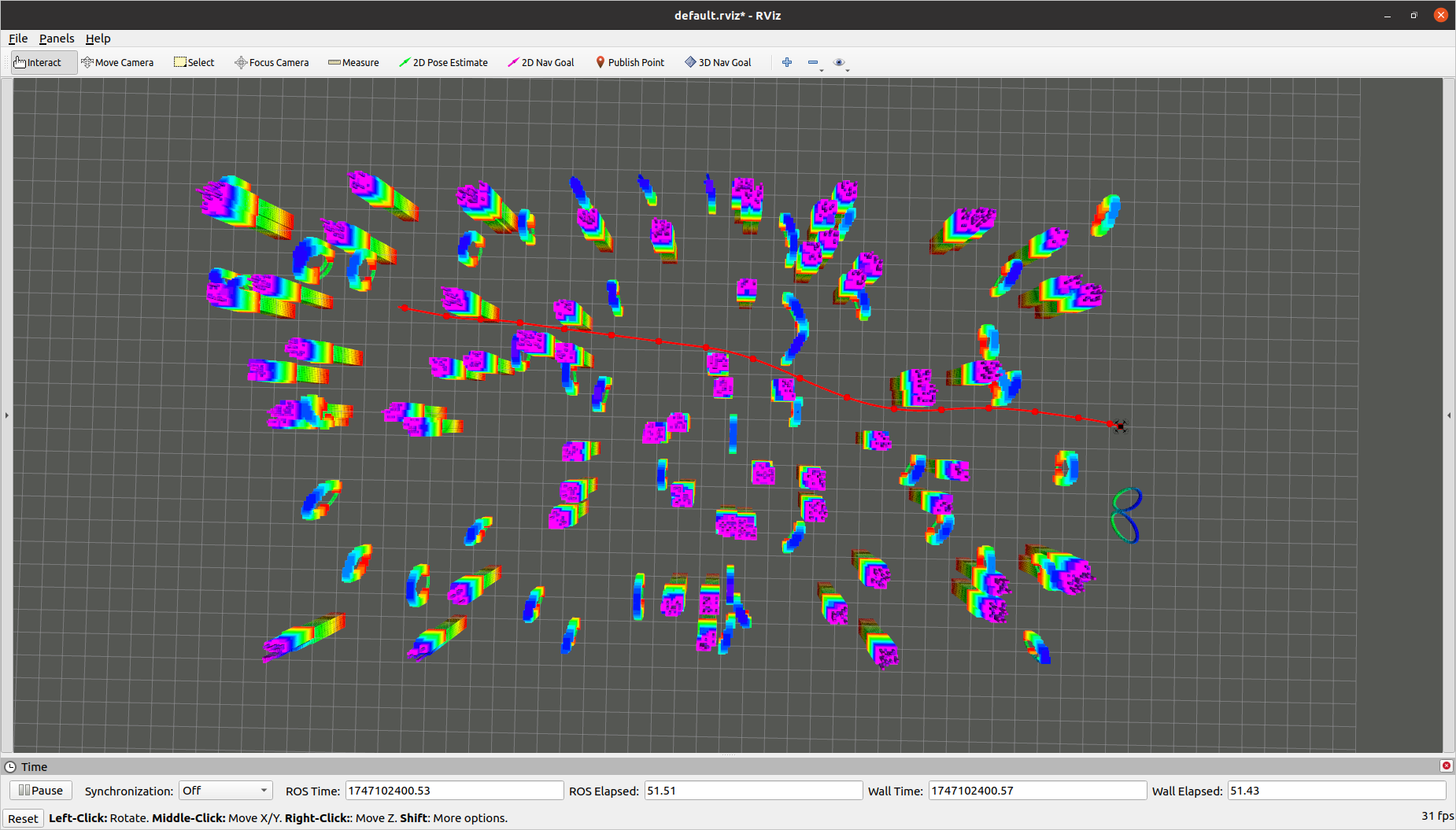
ROS 節點展示全局規劃和軌跡生成部分：

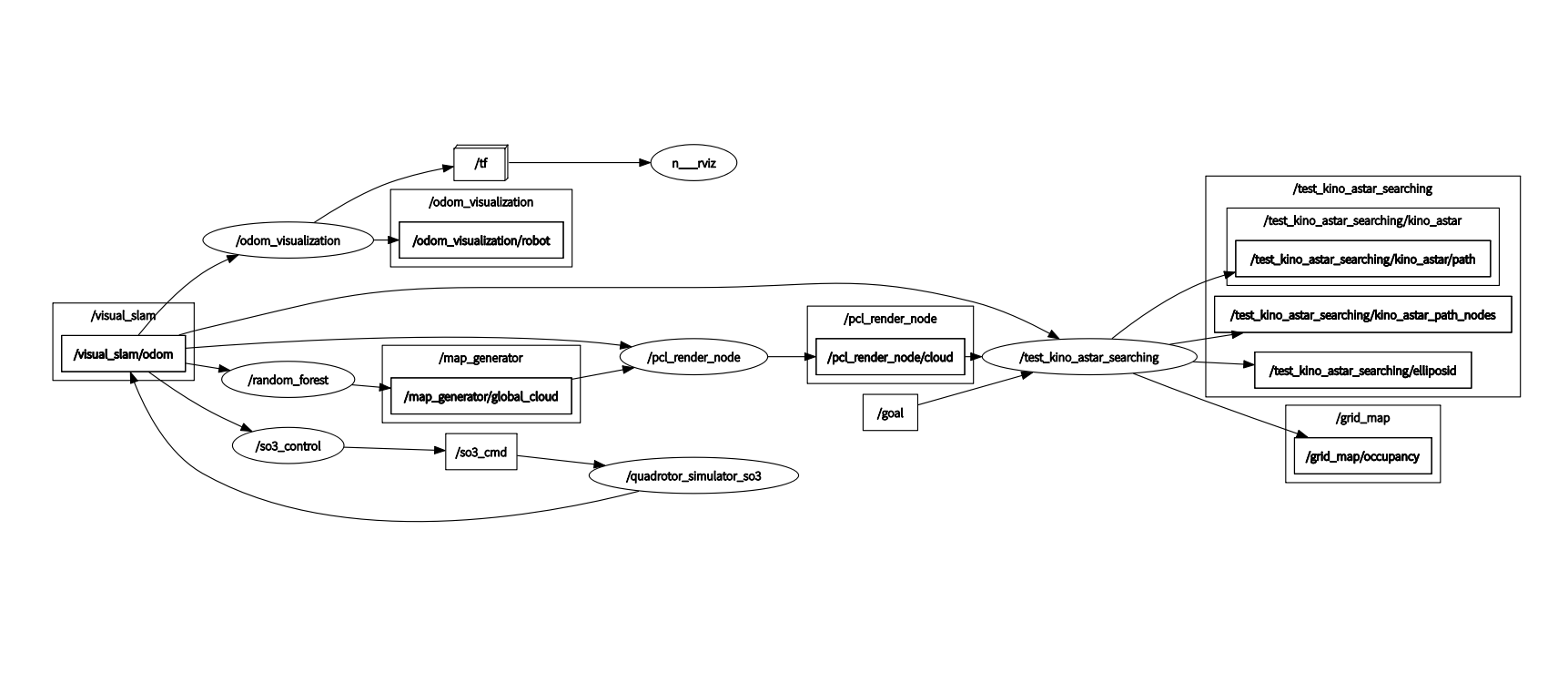
Kinodynamic A*代碼主體：

int KinoAstar::search(Eigen::Vector3d start_pt, Eigen::Vector3d start_vel,Eigen::Vector3d end_pt, Eigen::Vector3d end_vel,std::vector<Eigen::Vector3d>& path)
{// 記錄算法啟動時間，計算加速度分辨率倒數，初始化最優時間為無窮大ros::Time start_time = ros::Time::now();double inv_acc_res_ = 1.0 / acc_res_;double optimal_time = inf;// 從節點池中分配起點節點，設置位置、速度、索引、實際代價g_cost（起點到當前節點的累積代價）和綜合代價f_cost（g_cost + 啟發式代價）KinoAstarNodePtr start_node = path_node_pool_[use_node_num_];start_node->position = start_pt;start_node->velocity = start_vel;start_node->index = posToIndex(start_pt);start_node->g_cost = 0.0;start_node->f_cost = lambda_heu_ * getHeuristicCost(start_pt, start_vel, end_pt, end_vel, optimal_time);use_node_num_++;// 將起點加入優先隊列open_list_（按f_cost排序），并標記為“待擴展”open_list_.push(start_node);expanded_list_.insert(start_node->index, start_node);start_node->node_state = IN_OPEN_LIST_;std::vector<Eigen::Vector3d> path_nodes_list;while (!open_list_.empty()){// 循環處理開放列表，取出當前最優節點，移入關閉列表close_list_，標記為“已擴展”KinoAstarNodePtr current_node = open_list_.top();open_list_.pop();close_list_.insert(current_node->index, current_node);current_node->node_state = IN_CLOSE_LIST_;current_node->duration = sample_tau_;// debug// std::cout << "current_node: " << current_node->position.transpose() << std::endl;// check if near goal// 若當前節點接近終點，嘗試直接生成無碰撞的最優軌跡（如多項式插值或動力學可行路徑）if ((current_node->position - end_pt).norm() < goal_tolerance_){double tmp_cost = lambda_heu_ * getHeuristicCost(current_node->position, current_node->velocity, end_pt, end_vel, optimal_time);bool shot_path_found = computeShotTraj(current_node->position, current_node->velocity, end_pt, end_vel, optimal_time);// std::cout << "optimal_time: " << optimal_time << std::endl;if (shot_path_found){ros::Time end_time = ros::Time::now();std::cout << "kinodynamic path found, time cost: " << (end_time - start_time).toSec() << std::endl;std::cout << "use_node_num: " << use_node_num_ << std::endl;std::cout << "total_cost_J: " << current_node->g_cost + tmp_cost << std::endl;current_node->duration = optimal_time;std::vector<KinoAstarNodePtr> path_pool = retrievePath(current_node, path_nodes_list);path_nodes_list.push_back(end_pt);visPathNodes(path_nodes_list);switch (collision_check_type_){case 1: // grid map check{samplePath(path_pool, path);break;}case 2: // local cloud check{sampleEllipsoid(path_pool, path, rot_list);visEllipsoid(path, rot_list);break;}  }return REACH_END;}else if (current_node->parent != NULL){// std::cout << "near end!" << std::endl;}else{std::cout << "no shot path found, end searching" << std::endl;return NO_PATH_FOUND;   }// else continue;  }// expand current node// (2r+1)^3 samplefor (double ax = -max_accel_; ax <= max_accel_ + 1e-3; ax += inv_acc_res_ * max_accel_)for (double ay = -max_accel_; ay <= max_accel_ + 1e-3; ay += inv_acc_res_ * max_accel_)for (double az = -max_accel_; az <= max_accel_ + 1e-3; az += inv_acc_res_ * max_accel_){Eigen::Vector3d ut;ut << ax, ay, az;Eigen::Matrix<double, 6, 1> x0;x0.head(3) = current_node->position;x0.tail(3) = current_node->velocity;Eigen::Matrix<double, 6, 1> xt;int segment_num = std::floor(sample_tau_ / step_size_);bool flag = false;bool collision_flag = false;for (int i = 0; i <= segment_num; i++){double t = i * step_size_;StateTransit(x0, xt, ut, t);Eigen::Vector3d tmp_pos = xt.head(3);// check collision and if out of mapif (grid_map_->isInMap(tmp_pos) == false){flag = true;break;}// check collisionswitch (collision_check_type_){case 1: // grid map checkif (grid_map_->getInflateOccupancy(tmp_pos) == 1){collision_flag = true;break;}case 2: // local cloud checkif (isCollisionFree(tmp_pos, ut) == false){collision_flag = true;break;}}if (collision_flag){flag = true;break;}// check velocity limitif (xt.tail(3)(0) < -max_vel_ || xt.tail(3)(0) > max_vel_ || xt.tail(3)(1) < -max_vel_ || xt.tail(3)(1) > max_vel_ || xt.tail(3)(2) < -max_vel_ || xt.tail(3)(2) > max_vel_){flag = true;break;}}if (flag) continue;StateTransit(x0, xt, ut, sample_tau_);// std::cout << "xt: " << xt.head(3).transpose() << std::endl;// std::cout << "index: " << posToIndex(xt.head(3)).transpose() << std::endl;// check if in close_list_if (close_list_.find(posToIndex(xt.head(3))) != NULL){continue;}// check if in expanded_list_else if (expanded_list_.find(posToIndex(xt.head(3))) == NULL){KinoAstarNodePtr pro_node = path_node_pool_[use_node_num_];pro_node->position = xt.head(3);pro_node->velocity = xt.tail(3);pro_node->index = posToIndex(xt.head(3));pro_node->g_cost = current_node->g_cost + (ut.dot(ut) + rou_) * sample_tau_;pro_node->f_cost = pro_node->g_cost + lambda_heu_ * getHeuristicCost(pro_node->position, pro_node->velocity, end_pt, end_vel, optimal_time);pro_node->parent = current_node;pro_node->input = ut;pro_node->duration = sample_tau_;pro_node->node_state = IN_OPEN_LIST_;use_node_num_++;open_list_.push(pro_node);expanded_list_.insert(pro_node->index, pro_node);// check if use_node_num reach the max_node_numif (use_node_num_ >= allocated_node_num_){std::cout << "reach max node num, end searching" << std::endl;return NO_PATH_FOUND;}}else{// pruning, if in same grid, check if g_cost is smaller and updatedouble tmp_g_cost = current_node->g_cost + (ut.dot(ut) + rou_) * sample_tau_;KinoAstarNodePtr old_node = expanded_list_.find(posToIndex(xt.head(3)));if (tmp_g_cost < old_node->g_cost){old_node->position = xt.head(3);old_node->velocity = xt.tail(3);// old_node->index = posToIndex(xt.head(3));old_node->g_cost = tmp_g_cost;old_node->f_cost = old_node->g_cost + lambda_heu_ * getHeuristicCost(old_node->position, old_node->velocity, end_pt, end_vel, optimal_time);old_node->parent = current_node;old_node->input = ut;}}}}std::cout << "open_list is empty, end searching, no path found" << std::endl;return NO_PATH_FOUND;
}

?初始化階段：

ros::Time start_time = ros::Time::now();
double inv_acc_res_ = 1.0 / acc_res_;
double optimal_time = inf;

記錄算法啟動時間，計算加速度分辨率倒數，初始化最優時間為無窮大。

起點節點初始化：

KinoAstarNodePtr start_node = path_node_pool_[use_node_num_];
start_node->position = start_pt;
start_node->velocity = start_vel;
start_node->index = posToIndex(start_pt);
start_node->g_cost = 0.0;
start_node->f_cost = lambda_heu_ * getHeuristicCost(...);
use_node_num_++;

?從節點池中分配起點節點，設置位置、速度、索引、實際代價g_cost（起點到當前節點的累積代價）和綜合代價f_cost（g_cost + 啟發式代價）。

開放列表與擴展列表管理?：

open_list_.push(start_node);
expanded_list_.insert(start_node->index, start_node);
start_node->node_state = IN_OPEN_LIST_;

將起點加入優先隊列open_list_（按f_cost排序），并標記為“待擴展”。

主搜索循環?:

while (!open_list_.empty()) {
KinoAstarNodePtr current_node = open_list_.top();
open_list_.pop();
close_list_.insert(current_node->index, current_node);
current_node->node_state = IN_CLOSE_LIST_;

循環處理開放列表，取出當前最優節點，移入關閉列表close_list_，標記為“已擴展”。

終點檢查與軌跡優化?：

if ((current_node->position - end_pt).norm() < goal_tolerance_) {bool shot_path_found = computeShotTraj(...);if (shot_path_found) {samplePath(path_pool, path);return REACH_END;}
}

若當前節點接近終點，嘗試直接生成無碰撞的最優軌跡（如多項式插值或動力學可行路徑）。

samplePath：

主體部分：

void KinoAstar::samplePath(std::vector<KinoAstarNodePtr> path_pool, std::vector<Eigen::Vector3d>& path)
{// 當路徑池中有多個節點時（非單節點情況）if (path_pool.size() != 1){// 遍歷路徑池中相鄰的節點對for (int i = 0; i < path_pool.size() - 1; i++){KinoAstarNodePtr curr_node = path_pool[i];   // 當前路徑節點KinoAstarNodePtr next_node = path_pool[i + 1]; // 下一路徑節點double curr_t = 0.0;  // 當前時間戳Eigen::Matrix<double, 6, 1> x0, xt; // 狀態向量（6維：位置+速度）x0 << curr_node->position, curr_node->velocity; // 初始化當前狀態// 根據節點持續時間分割時間段（基于固定步長step_size_）int segment_num = std::floor(curr_node->duration / step_size_);// 逐時間段生成路徑點for (int j = 0; j < segment_num; j++){curr_t = j * step_size_;  // 計算當前時間StateTransit(x0, xt, next_node->input, curr_t); // 狀態轉移計算（可能涉及運動學方程）[1,5](@ref)path.push_back(xt.head(3));  // 將位置信息(x,y,z)加入路徑集合}// 處理最后一個時間段（可能不完整的步長）StateTransit(x0, xt, next_node->input, curr_node->duration);// 驗證最終狀態與目標節點的位置一致性if ((xt.head(3) - next_node->position).norm() > 1e-2){std::cerr << "error in sample!" << std::endl; // 超閾值報錯}}// 處理路徑池中最后一個節點的軌跡KinoAstarNodePtr last_node = path_pool.back();double td = last_node->duration;  // 獲取總持續時間Eigen::Matrix<double, 4, 1> t_vector; // 時間多項式向量（t^0, t^1, t^2, t^3）// 分割時間段生成路徑點int segment_num = std::floor(td / step_size_);double curr_t = 0.0;for (int j = 0; j <= segment_num; j++){curr_t = j * step_size_;  // 當前時間戳for (int i = 0; i < 4; i++) {t_vector(i) = pow(curr_t, i); // 構建時間多項式項（如t3, t2, t, 1）}Eigen::Vector3d shot_pos = shot_coef_ * t_vector; // 通過多項式系數生成路徑點（軌跡插值）[5](@ref)path.push_back(shot_pos); // 將插值點加入路徑}}else  // 當路徑池只有單個節點時的處理邏輯{KinoAstarNodePtr last_node = path_pool.back();double td = last_node->duration;  // 總持續時間Eigen::Matrix<double, 4, 1> t_vector; // 同上時間多項式向量int segment_num = std::floor(td / step_size_);double curr_t = 0.0;for (int j = 0; j <= segment_num; j++) {curr_t = j * step_size_;for (int i = 0; i < 4; i++) {t_vector(i) = pow(curr_t, i);}Eigen::Vector3d shot_pos = shot_coef_ * t_vector; // 多項式軌跡生成path.push_back(shot_pos);}}
}

?該函數主要用于：

  1. ??路徑采樣??：根據路徑池（path_pool）中的節點，通過時間分片（step_size_）生成連續路徑點。
  2. ??狀態轉移??：在多節點情況下，通過StateTransit函數計算相鄰節點間的運動狀態（可能包含速度/加速度模型）
  3. ??軌跡插值??：在單節點或最終階段，利用四次多項式系數（shot_coef_）生成平滑軌跡，適用于機器人/自動駕駛的運動規劃
  4. ??錯誤校驗??：檢查采樣結果與目標節點的位置偏差，確保路徑精度。

getHeuristicCost：

主體部分：

double KinoAstar::getHeuristicCost(Eigen::Vector3d x1, Eigen::Vector3d v1,Eigen::Vector3d x2, Eigen::Vector3d v2,double &optimal_time)
{Eigen::Vector3d dp = x2 - x1;double optimal_cost = inf;double a = -36 * dp.dot(dp);double b = 24 * dp.dot(v1 + v2);double c = -4 * (v1.dot(v1) + v1.dot(v2) + v2.dot(v2));double d = 0;double e = rou_;std::vector<double> dts = quartic(e, d, c, b, a);double T_bar = ((x1 - x2).lpNorm<Eigen::Infinity>() / max_vel_);for (int i = 0; i < dts.size(); i++){double t = dts[i];double tmp_cost = a / (-3 * t * t * t) + b / (-2 * t * t) + c / (-1 * t) + e * t;if (tmp_cost < optimal_cost && t > T_bar && tmp_cost > 0){optimal_cost = tmp_cost;optimal_time = t;}}return tie_breaker_ * optimal_cost;}

?KinoAstar::getHeuristicCost?是運動規劃中結合動力學約束的啟發式函數，其核心目標是??通過最優控制理論計算從當前狀態到目標狀態的最小控制能量代價??，用于引導A*算法的搜索方向并加速收斂。以下是逐層解析：

函數參數與目標?：

  • 輸入參數??：
    • x1/v1：起點位置和速度
    • x2/v2：終點位置和速度
    • optimal_time（輸出）：最優時間估計
  • ??輸出??：啟發式代價（預估最小控制能量）

?數學原理：最優控制問題建模?：

?該函數基于??龐特里亞金極小值原理??（Pontryagin's Minimum Principle），求解兩點邊界最優控制問題（OBVP）。目標是最小化控制能量（如加加速度的積分），同時滿足位置和速度的終點約束。

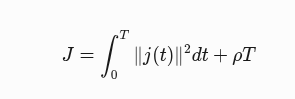
其中：

  • j(t)?是加加速度（控制輸入）
  • ρ?是時間權重（對應代碼中的?rou_）

通過狀態方程和協態方程推導，最終得到關于時間?T?的??四次多項式方程??，其根對應可能的極值點。

代碼實現步驟?：

  1. 構造四次方程系數??：

    • 計算位置差?dp = x2 - x1
    • 根據幾何關系和控制能量積分，生成系數?a, b, c, d, e（對應四次方程?aT^4+bT^3+cT^2+d^T+e=0）

  2. ??求解方程根??：

    • 調用?quartic(e, d, c, b, a)?解四次方程，得到候選時間解?dts。

  3. ??篩選最優時間與代價??：

    • 計算時間下限?T_bar（確保速度不超過最大值?max_vel_）
    • 遍歷所有候選時間?t，計算對應的能量代價?tmp_cost，篩選滿足?t>T_bar?的最小代價?optimal_cost?及對應時間?optimal_time。

  4. ??返回加權代價??：

    • 最終代價乘以?tie_breaker_（通常略大于1的系數，避免路徑重復擴展）

computeShotTraj：

主體部分：

bool KinoAstar::computeShotTraj(Eigen::Vector3d x1, Eigen::Vector3d v1,Eigen::Vector3d x2, Eigen::Vector3d v2,double optimal_time)
{double td = optimal_time;Eigen::Vector3d dp = x2 - x1;Eigen::Vector3d dv = v2 - v1;shot_coef_.col(0) = x1;shot_coef_.col(1) = v1;shot_coef_.col(2) = 0.5 * (6 / (td * td) * (dp - v1 * td) - 2 * dv / td);shot_coef_.col(3) = 1.0 / 6.0 * (-12 / (td * td *td) * (dp - v1 * td) + 6 * dv / (td * td));Eigen::Matrix<double, 4, 4> Transit_v;Transit_v << 0, 0, 0, 0, 1, 0, 0, 0,0, 2, 0, 0, 0, 0, 3, 0;Eigen::Matrix<double, 4, 4> Transit_a;Transit_a << 0, 0, 0, 0, 1, 0, 0, 0,0, 2, 0, 0, 0, 0, 0, 0;vel_coef_ = shot_coef_ * Transit_v;acc_coef_ = vel_coef_ * Transit_a;Eigen::Matrix<double, 4, 1> t_vector;int segment_num = std::floor(td / step_size_);double curr_t = 0.0;for (int j = 0; j <= segment_num; j++){curr_t = j * step_size_;for (int i = 0; i < 4; i++){t_vector(i) = pow(curr_t, i);}Eigen::Vector3d shot_pos = shot_coef_ * t_vector;Eigen::Vector3d shot_vel = vel_coef_ * t_vector;Eigen::Vector3d shot_acc = acc_coef_ * t_vector;// check collisionif (grid_map_->getInflateOccupancy(shot_pos)){return false;}// only check collision, vel and acc limit by limit T_// // check velocity limit// if (shot_vel(0) > max_vel_ || shot_vel(0) < -max_vel_ || //     shot_vel(1) > max_vel_ || shot_vel(1) < -max_vel_ || //     shot_vel(2) > max_vel_ || shot_vel(2) < -max_vel_)// {//   return false;// }// // check acceleration limit// if (shot_acc(0) > max_accel_ || shot_acc(0) < -max_accel_ || //     shot_acc(1) > max_accel_ || shot_acc(1) < -max_accel_ || //     shot_acc(2) > max_accel_ || shot_acc(2) < -max_accel_)// {//   return false;// }}return true;
}

?定義了一個函數computeShotTraj，屬于類KinoAstar：

bool KinoAstar::computeShotTraj(Eigen::Vector3d x1, Eigen::Vector3d v1,Eigen::Vector3d x2, Eigen::Vector3d v2,double optimal_time)

?該函數用于計算一步到位的航跡，參數包括初始位置x1、初始速度v1、目標位置x2、目標速度v2，以及最優時間optimal_time，返回值為布爾類型。

double td = optimal_time;

將optimal_time賦值給變量td，表示軌跡的時間長度。

Eigen::Vector3d dp = x2 - x1;
Eigen::Vector3d dv = v2 - v1;

計算位置差和速度差。

shot_coef_.col(0) = x1;
shot_coef_.col(1) = v1;
shot_coef_.col(2) = 0.5 * (6 / (td * td) * (dp - v1 * td) - 2 * dv / td);
shot_coef_.col(3) = 1.0 / 6.0 * (-12 / (td * td *td) * (dp - v1 * td) + 6 * dv / (td * td));

?將初始位置x1和初始速度v1賦值給shot_coef_的第一列和第二列，shot_coef_是一個用于存儲三次多項式系數的矩陣。計算三次多項式的第二項系數，涉及位置差dp、初始速度v1、速度差dv，以及時間td的計算。

Eigen::Matrix<double, 4, 4> Transit_v;Transit_v << 0, 0, 0, 0, 1, 0, 0, 0,0, 2, 0, 0, 0, 0, 3, 0;Eigen::Matrix<double, 4, 4> Transit_a;Transit_a << 0, 0, 0, 0, 1, 0, 0, 0,0, 2, 0, 0, 0, 0, 0, 0;

定義一個4x4的矩陣Transit_v，用于將位置系數轉換為速度系數。矩陣的結構是根據速度的導數特性定義的。定義一個4x4的矩陣Transit_a，用于將速度系數轉換為加速度系數。矩陣的結構是根據加速度的導數特性定義的。

vel_coef_ = shot_coef_ * Transit_v;
acc_coef_ = vel_coef_ * Transit_a;

通過shot_coef_和Transit_v的矩陣乘法，計算出速度系數矩陣vel_coef_。?通過vel_coef_和Transit_a的矩陣乘法，計算出加速度系數矩陣acc_coef_。

Eigen::Matrix<double, 4, 1> t_vector;
int segment_num = std::floor(td / step_size_);
double curr_t = 0.0;
for (int j = 0; j <= segment_num; j++){curr_t = j * step_size_;for (int i = 0; i < 4; i++){t_vector(i) = pow(curr_t, i);}Eigen::Vector3d shot_pos = shot_coef_ * t_vector;Eigen::Vector3d shot_vel = vel_coef_ * t_vector;Eigen::Vector3d shot_acc = acc_coef_ * t_vector;// check collisionif (grid_map_->getInflateOccupancy(shot_pos)){return false;}

?定義一個4x1的矩陣t_vector，用于存儲時間的冪次計算。計算時間分割數segment_num，即時間td除以步長step_size_并向下取整。循環遍歷時間分割點，從0到segment_num。計算當前時間curr_t，即j乘以步長step_size_。通過shot_coef_和t_vector的矩陣乘法，計算出當前位置shot_pos。通過vel_coef_和t_vector的矩陣乘法，計算出當前速度shot_vel。通過acc_coef_和t_vector的矩陣乘法，計算出當前加速度shot_acc。檢查當前位置shot_pos是否與網格地圖中的膨脹障礙物發生碰撞。如果發生碰撞，返回false，表示軌跡不可行。

retrievePath：

主體部分：

std::vector<KinoAstarNodePtr> KinoAstar::retrievePath(KinoAstarNodePtr end_node, std::vector<Eigen::Vector3d>& path_nodes_list)
{KinoAstarNodePtr current_node = end_node;std::vector<KinoAstarNodePtr> path_nodes;while (current_node->parent != NULL){path_nodes.push_back(current_node);path_nodes_list.push_back(current_node->position);current_node = current_node->parent;}path_nodes.push_back(current_node);path_nodes_list.push_back(current_node->position);std::reverse(path_nodes.begin(), path_nodes.end());std::reverse(path_nodes_list.begin(), path_nodes_list.end());return path_nodes;
}
std::vector<KinoAstarNodePtr> path_pool = retrievePath(current_node, path_nodes_list);

這段代碼定義了一個函數 retrievePath，屬于類 KinoAstar，用于從終點節點回溯并提取出路徑上的所有節點以及它們的位置，形成完整的路徑。

  1. 路徑回溯：從終點節點開始，通過每個節點的parent指針逐級向上訪問，直到找到起點（即parent為NULL的節點）。
  2. 路徑構建：在回溯過程中，將每個節點及其位置分別添加到path_nodes和path_nodes_list中。
  3. 順序調整：由于回溯得到的路徑是從終點到起點的順序，使用std::reverse將兩個向量反轉，最終得到從起點到終點的正確路徑順序。

?節點擴展與狀態轉移：

for (double ax = -max_accel_; ...) {Eigen::Vector3d ut(ax, ay, az);StateTransit(x0, xt, ut, sample_tau_);// 碰撞檢測與速度限制檢查
}

?功能??：遍歷所有可能的加速度控制輸入（三維離散化），生成子節點狀態

  • 關鍵點??：
    • ??狀態轉移方程??：StateTransit根據動力學模型（如勻加速運動學）計算下一時刻狀態
    • ??碰撞檢測??：分段檢查軌跡段是否在自由空間內（grid_map_或點云檢測）

StateTransit：?

主體部分：

void KinoAstar::StateTransit(Eigen::Matrix<double, 6, 1> &x0, Eigen::Matrix<double, 6, 1> &xt,Eigen::Vector3d ut, double t)
{// 初始化6x6狀態轉移矩陣e_At為單位矩陣（初始狀態下時間t=0時的狀態轉移）Eigen::Matrix<double, 6, 6> e_At = Eigen::Matrix<double, 6, 6>::Identity();// 前三行的位置-速度關系處理：位置 += 速度 * 時間t（例如x = x0 + vx*t）for (int i = 0; i < 3; i++) {e_At(i, 3 + i) = t;  // 例如e_At矩陣第0行第3列設為t，對應x方向的位置增量}// 初始化6x3的積分矩陣（用于控制輸入ut對狀態的影響）Eigen::Matrix<double, 6, 3> Integral = Eigen::Matrix<double, 6, 3>::Zero();// 填充積分矩陣：// 前三行對角線元素為0.5*t2（加速度對位置的影響，如Δx = 0.5*a*t2）// 后三行對角線元素為t（加速度對速度的影響，如Δv = a*t）for (int i = 0; i < 6; i++) {if (i < 3) Integral(i, i) = 0.5 * t * t;  // 位置積分項else Integral(i, i - 3) = t;         // 速度積分項}// 狀態轉移方程：xt = e_At * x0 + Integral * ut// 其中：// - e_At * x0 表示初始狀態的線性傳播（位置+速度）// - Integral * ut 表示控制輸入（如加速度）對狀態的影響xt = e_At * x0 + Integral * ut;
}

功能總結：

  1. ??狀態轉移模型??
    基于線性運動學模型，通過矩陣運算實現狀態預測。假設系統為二階模型（包含位置和速度），控制輸入ut可能對應加速度

  2. ??矩陣作用??

    • ??e_At??：6x6矩陣，描述位置和速度隨時間變化的線性關系（如勻速運動模型）。
    • ??Integral??：6x3矩陣，計算控制輸入對狀態的積分貢獻（如勻加速運動中的位移和速度變化）

  3. ??物理意義??
    假設系統狀態為[x, y, z, vx, vy, vz]，控制輸入為加速度[ax, ay, az]，則：

    • 位置更新：x_new = x0 + vx*t + 0.5*ax*t2
    • 速度更新：vx_new = vx + ax*t

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/pingmian/80882.shtml
繁體地址，請注明出處：http://hk.pswp.cn/pingmian/80882.shtml
英文地址，請注明出處：http://en.pswp.cn/pingmian/80882.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Transformer Decoder-Only 算力FLOPs估計

Transformer Decoder-Only 算力FLOPs估計

FLOPs和FLOPS的區別 FLOPs &#xff08;Floating Point Operations&#xff09;是指模型或算法執行過程中總的浮點運算次數&#xff0c;單位是“次”FLOPS &#xff08;Floating Point Operations Per Second&#xff09;是指硬件設備&#xff08;如 GPU 或 CPU&#xff09;每…
閱讀更多...
掌握MySQL數據庫操作：從創建到管理全攻略

掌握MySQL數據庫操作：從創建到管理全攻略

1.庫的操作 1.1庫的查看 show databases; 這句語法形式是查看服務器已經存在的數據庫 注意要加分號————&#xff1b; 1.databeses是復數形式 2.大小寫都可以 前提&#xff08;數據庫已經創建或查看服務器自帶的數據庫&#xff09; 也可以查看指定的數據庫 show cre…
閱讀更多...
服務器綜合實驗（實戰詳解）

服務器綜合實驗（實戰詳解）

實驗內容 環境拓撲結構 主機環境描述 主機名主機地址需要提供的服務content.exam.com172.25.250.101提供基于httpd/nginx的YUM倉庫服務ntp.exam.com172.25.250.102提供基于Chronyd的NTP服務mysql.exam.com172.25.250.103提供基于MYSQL的數據庫服務nfs.exam.com172.25.250.104…
閱讀更多...
CentOS 7 修改鎖屏時間為永不

CentOS 7 修改鎖屏時間為永不

在 CentOS 7 中&#xff0c;默認情況下&#xff0c;系統會在一定時間不活動后自動鎖屏。對于某些用戶來說&#xff0c;可能希望禁用自動鎖屏功能或者將鎖屏時間設置為“永不”。本文將介紹如何通過圖形界面和命令行兩種方式修改 CentOS 7 的鎖屏時間&#xff0c;確保系統永不自…
閱讀更多...
MySQL 日期計算方法 date_sub()、date_add()、datediff() 詳解-文中有示例幫助理解

MySQL 日期計算方法 date_sub()、date_add()、datediff() 詳解-文中有示例幫助理解

1、date_sub()、date_add() date_sub() 和date_add() 語法相同&#xff0c;只不過一個加一個減。 從日期中減去指定時間間隔 語法&#xff1a; DATE_SUB(start_date, INTERVAL expr unit) start_date: 起始日期&#xff08;如 now() , 字段名&#xff09;。 INTERVAL expr…
閱讀更多...
寶塔基于亞馬遜云服務器安裝mysql5.7失敗問題記錄

寶塔基于亞馬遜云服務器安裝mysql5.7失敗問題記錄

安裝日志如下&#xff1a; --2025-05-14 15:25:15-- https://na1-node.bt.cn/install/1/mysql.sh Resolving na1-node.bt.cn (na1-node.bt.cn)... 128.1.164.196 Connecting to na1-node.bt.cn (na1-node.bt.cn)|128.1.164.196|:443... connected. HTTP request sent, awaitin…
閱讀更多...
LLaMA-Factory 微調 Qwen2-7B-Instruct

LLaMA-Factory 微調 Qwen2-7B-Instruct

一、系統環境 使用的 autoDL 算力平臺 1、下載基座模型 pip install -U huggingface_hub export HF_ENDPOINThttps://hf-mirror.com # &#xff08;可選&#xff09;配置 hf 國內鏡像站huggingface-cli download --resume-download shenzhi-wang/Llama3-8B-Chinese-Chat -…
閱讀更多...
Redis三種高可用模式的使用場景及特點的詳細介紹

Redis三種高可用模式的使用場景及特點的詳細介紹

Redis三種高可用模式的使用場景及特點的詳細介紹&#xff0c;結合不同業務需求提供選擇建議&#xff1a; 主從模式&#xff08;Replication&#xff09; 核心能力&#xff1a;數據冗余備份、讀寫分離 適用場景&#xff1a; 讀多寫少&#xff1a;例如內容發布平臺、新聞網站等…
閱讀更多...
通俗易懂版知識點：Keepalived + LVS + Web + NFS 高可用集群到底是干什么的？

通俗易懂版知識點：Keepalived + LVS + Web + NFS 高可用集群到底是干什么的？

實驗開始前&#xff0c;先搞懂為什么要部署該集群&#xff1f; 這個方案的目標是讓網站 永不宕機&#xff0c;即使某臺服務器掛了&#xff0c;用戶也感覺不到。它主要涉及 負載均衡&#xff08;LVS&#xff09; 高可用&#xff08;Keepalived&#xff09; 共享存儲&#xff…
閱讀更多...
Qt中解決UI線程阻塞導致彈窗無法顯示的兩種方法

Qt中解決UI線程阻塞導致彈窗無法顯示的兩種方法

在Qt應用程序開發中，我們經常會遇到這樣的問題：當執行一個耗時操作時，整個界面會卡住，無法響應任何用戶操作，甚至連一個簡單的提示彈窗都無法正常顯示。本文將介紹兩種解決這個問題的方法，并通過完整的代碼示例進行說明。 問題描述 先來看一個常見的錯誤示例： #inclu…
閱讀更多...
2025年中國DevOps工具選型指南：主流平臺能力橫向對比

2025年中國DevOps工具選型指南：主流平臺能力橫向對比

在數字化轉型縱深發展的2025年&#xff0c;中國企業的DevOps工具選型呈現多元化態勢。本文從技術架構、合規適配、生態整合三個維度&#xff0c;對Gitee、阿里云效&#xff08;云效DevOps&#xff09;、GitLab CE&#xff08;中國版&#xff09;三大主流平臺進行客觀對比分析&a…
閱讀更多...
isp流程介紹(yuv格式階段)

isp流程介紹(yuv格式階段)

一、前言介紹 前面兩章里面&#xff0c;已經分別講解了在Raw和Rgb域里面&#xff0c;ISP的相關算法流程&#xff0c;從前面文章里面可以看到&#xff0c;在Raw和Rgb域里面&#xff0c;很多ISP算法操作&#xff0c;更像是屬于sensor矯正或者說sensor標定操作。本質上來說&#x…
閱讀更多...
虛幻引擎5-Unreal Engine筆記之UE編輯器退出時的保存彈框

虛幻引擎5-Unreal Engine筆記之UE編輯器退出時的保存彈框

虛幻引擎5-Unreal Engine筆記之UE編輯器退出時的保存彈框 code review! 文章目錄 虛幻引擎5-Unreal Engine筆記之UE編輯器退出時的保存彈框1. 退出編輯器時彈出的“Save Content”窗口2. File 菜單中的保存選項3. 區別總結 1. 退出編輯器時彈出的“Save Content”窗口 退出時…
閱讀更多...
如何判斷IP是否被平臺標記

如何判斷IP是否被平臺標記

一、基礎檢測&#xff1a;連通性與黑名單篩查 網絡連通性測試 Ping與Traceroute&#xff1a;通過命令測試延遲和路由路徑&#xff0c;若延遲>50ms或存在異常節點&#xff08;如某跳延遲>200ms&#xff09;&#xff0c;可能影響可用性。示例命令&#xff1a; bash ping 8.…
閱讀更多...
零Gas授權實戰：用線下簽名玩轉智能合約 Permit 機制

零Gas授權實戰：用線下簽名玩轉智能合約 Permit 機制

目錄 鏈下簽名背景什么是 Permit ？鏈下簽名應用場景Permit 原理簡述實戰：從合約到前端完整實現安全注意事項總結鏈下簽名背景 在以太坊智能合約開發中，很多初學者經常面臨這樣一個問題：ERC20 代幣授權必須先調用鏈上合約的 approve()，再調用鏈上合約的 transferFrom()，每…
閱讀更多...
React 簡介：核心概念、組件化架構與聲明式編程

React 簡介：核心概念、組件化架構與聲明式編程

本文為《React Agent&#xff1a;從零開始構建 AI 智能體》專欄系列文章。 專欄地址&#xff1a;https://blog.csdn.net/suiyingy/category_12933485.html。項目地址&#xff1a;https://gitee.com/fgai/react-agent&#xff08;含完整代碼示?例與實戰源&#xff09;。完整介紹…
閱讀更多...
LeetCode100.7 接雨水

LeetCode100.7 接雨水

對于這題&#xff0c;有一個非常直觀簡潔的思路&#xff1a;水量等于柱子圍成的體積減去柱子的體積。 首先計算每一個高度的體積&#xff0c;相加即為總體積&#xff0c;減去sum(height)即為水的體積。 class Solution { public:int trap(vector<int>& height) {in…
閱讀更多...
NineData 社區版 V4.1.0 正式發布，新增 4 條遷移鏈路，本地化數據管理能力再升級

NineData 社區版 V4.1.0 正式發布，新增 4 條遷移鏈路，本地化數據管理能力再升級

NineData 社區版 V4.1.0 正式更新發布。本次通過新增 4 條遷移鏈路擴展、國產數據庫深度適配、敏感數據保護增強?等升級&#xff0c;進一步鞏固了其作為高效、安全、易用的數據管理工具的定位。無論是開發測試、數據遷移&#xff0c;還是多環境的數據管理&#xff0c;NineData…
閱讀更多...
Go 語言 sqlx 庫使用：對 MySQL 增刪改查

Go 語言 sqlx 庫使用：對 MySQL 增刪改查

MySQL 作為目前最流行的開源關系型數據庫&#xff0c;其 SQL 語法體系已形成行業標準&#xff0c;相關知識體系龐大且成熟&#xff0c;本文不再對 SQL 基礎進行詳細展開&#xff0c;建議尚未掌握的讀者先行系統學習。本文聚焦于如何使用 Go 語言進行 MySQL 數據庫操作&#xff…
閱讀更多...
單片機-STM32部分：13、PWM

單片機-STM32部分：13、PWM

飛書文檔https://x509p6c8to.feishu.cn/wiki/NjhuwbVP7iaEOikVK95cmJNLnWf PWM&#xff08;Pulse Width Modulation&#xff09;脈沖寬度調制&#xff0c;是利用微處理器的數字輸出來對模擬電路進行控制的一種非常有效的技術。它是把每一脈沖寬度均相等的脈沖列作為PWM波形&am…
閱讀更多...
最新文章

Copyright @ 2022~2023