PyMC+AI提示詞貝葉斯項目反應IRT理論Rasch分析籃球比賽官方數據：球員能力與位置層級結構研究

全文鏈接：tecdat.cn/?p=41666

在體育數據分析領域不斷發展的當下，數據科學家們致力于挖掘數據背后的深層價值，為各行業提供更具洞察力的決策依據。近期，我們團隊完成了一項極具意義的咨詢項目，旨在通過先進的數據分析手段，深入探究籃球比賽中犯規判罰的內在規律（點擊文末“閱讀原文”獲取完整代碼、數據、文檔）。

本專題文章圍繞籃球犯規判罰數據展開研究，運用貝葉斯項目反應理論（Bayesian Item Response Theory，IRT），結合 PyMC 軟件強大的建模能力，對官方 2015 - 2021 年籃球比賽相關報告數據進行了全面分析。在項目過程中，我們首先對原始數據進行細致的收集與處理，提取關鍵信息；接著構建拉施模型（Rasch Model），定義模型參數并利用 PyMC 實現模型搭建；隨后通過后驗采樣與收斂檢查確保模型的可靠性；最后對后驗結果進行多維度分析，不僅發現了模型中部分池化的效果，還揭示了球員表現與位置之間的潛在關系，為籃球比賽的策略制定和裁判判罰研究提供了新的視角。

專題項目文件已分享在交流社群，閱讀原文進群和 500 + 行業人士共同交流和成長。在這里，您可以與眾多志同道合的數據愛好者、行業專家一同探討數據分析在體育領域的應用，碰撞思維的火花，共同推動數據分析技術在各行業的發展與創新。

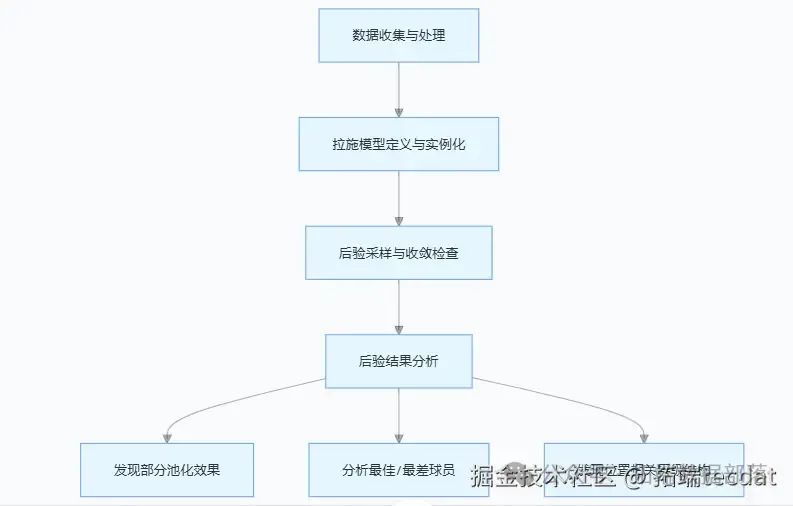
文章脈絡：

在籃球比賽中，犯規判罰是一個重要且復雜的環節。每一次犯規判罰的背后，都涉及到不同角色球員之間的互動，比如犯規球員和被侵犯球員。而這些判罰結果不僅與球員的角色有關，還可能與每個球員自身的潛在能力相關。那么，如何研究這種涉及眾多球員、具有層級結構的多主體互動場景呢？
貝葉斯項目反應理論結合現代強大的統計軟件為我們提供了一種優雅且有效的建模選擇。接下來，我們將詳細介紹如何運用該理論對籃球犯規判罰數據進行分析。

動機

在籃球比賽中，我們觀察到的是一個二元結果，即犯規是否被吹罰，這一結果來自于兩個不同角色球員（犯規球員和被侵犯球員）在一次籃球進攻中的互動。而且，每個犯規或被侵犯的球員可能會在多次進攻中被觀察到。所以，我們希望估計每個球員作為犯規或被侵犯球員時，其潛在能力對觀察到的判罰結果的貢獻。通過這種方式，我們可以對球員進行從高到低的排名，量化排名中的不確定性，并發現犯規判罰中涉及的額外層級結構。

拉施模型（Rasch Model）

我們的數據來源于官方的籃球比賽相關報告，涵蓋了2015年到2021年期間的比賽數據。在這個數據集中，每一行數據代表一次進攻，涉及兩名球員（犯規球員和被侵犯球員），并且記錄了這次進攻中犯規是否被吹罰。
我們為每個球員定義了兩個潛在變量：

theta
：用于估計球員在被侵犯時被吹罰犯規的能力。
b
：用于估計球員在犯規時不被吹罰犯規的能力。
這兩個參數的值越高，對該球員所在的球隊越有利。我們使用標準的拉施模型來估計這兩個參數，假設在第k次進攻中，裁判吹罰犯規的對數幾率比等于相應球員的theta-b。同時，我們對所有的theta和b設置了層級超先驗，以考慮球員之間的共享能力以及不同球員的觀察數量差異。

分析過程

我們的分析主要包括以下四個步驟：數據收集與處理、拉施模型的定義與實例化、后驗采樣與收斂檢查、后驗結果分析。

數據收集與處理

首先，我們從原始數據集中導入數據。我們只導入了五列數據，分別是：

committing
：犯規球員的名字。
disadvantaged
：被侵犯球員的名字。
decision
：對這次進攻的判定結果，有四個取值：CNC（正確未吹罰）、INC（錯誤未吹罰）、IC（錯誤吹罰）、CC（正確吹罰）。
committing_position
：犯規球員的位置，取值包括G（后衛）、F（前鋒）、C（中鋒）、G-F、F-G、F-C、C-F。
disadvantaged_position
：被侵犯球員的位置，取值與犯規球員位置類似。
我們已經從原始數據集中刪除了涉及球員少于兩名的進攻（比如走步或違例），并且原始數據集不包含球員位置信息，這是我們自己添加的。
以下是部分數據導入的代碼（AI提示詞：使用Python的pandas庫從指定路徑或數據獲取函數導入籃球犯規數據）：

csharp
代碼解讀
復制代碼
try:df_orig = pd.read_csv(os.path.join("..",?"data", sponse_nba.csv"), index_col=0)
except FileNotFoundError:df_orig = pd.read_csv(pm.get_data("itemnba.csv"), index_col=0)
df_orig.head()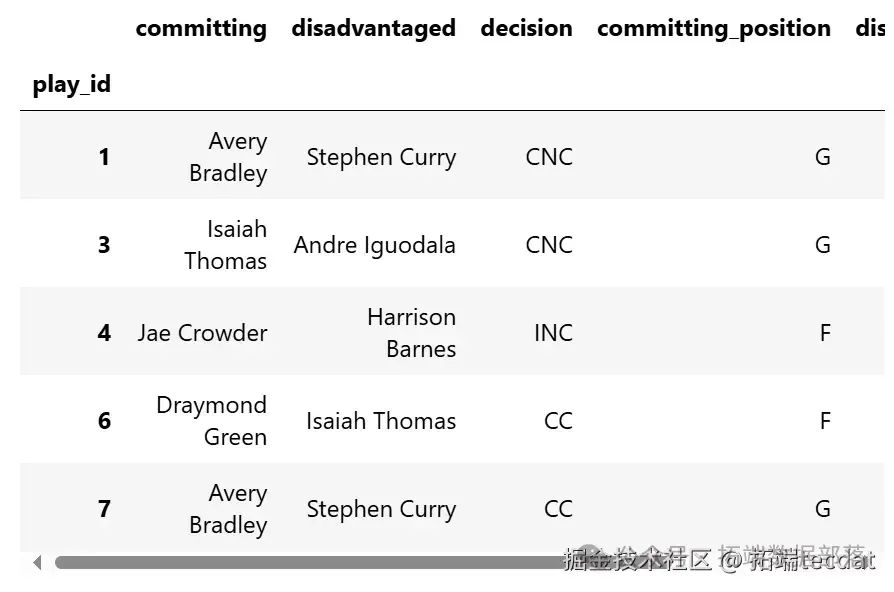

接下來，我們對數據進行三步處理：

創建一個數據框df，刪除df_orig中的位置信息；同時創建一個數據框df_position，收集所有球員及其相應位置（這個數據框在筆記本的最后才會用到）。
向df添加一個名為foul_called的列，如果一次進攻中吹罰了犯規，則該列賦值為1，否則為0。
為犯規球員和被侵犯球員分配ID，并使用這個索引來識別每次觀察到的進攻中的相應球員。
以下是數據處理的部分代碼（AI提示詞：使用Python的pandas庫對導入的籃球犯規數據進行處理，包括創建新數據框、添加新列、對球員進行索引等操作）：

項目反應模型

模型定義

我們用以下符號表示：

(N_d)和(N_c)分別表示被侵犯球員和犯規球員的數量。
(K)表示進攻的次數。
(k)表示一次進攻。
(y_k)表示在第(k)次進攻中觀察到的犯規判罰結果（吹罰或未吹罰）。
(p_k)表示在第(k)次進攻中吹罰犯規的概率。
(i(k))表示第(k)次進攻中的被侵犯球員。
(j(k))表示第(k)次進攻中的犯規球員。
我們假設每個被侵犯球員由潛在變量(\theta_i)（(i = 1,2,…,N_d)）描述，每個犯規球員由潛在變量(b_j)（(j = 1,2,…,N_c)）描述。
然后，我們將每個觀察值(y_k)建模為獨立伯努利試驗的結果，其概率為(p_k)，其中：
[ p_k = \text{sigmoid}(\eta_k) = \left(1 + e{-\eta_k}\right){-1}, \quad \text{with} \quad \eta_k = \theta_{i(k)} - b_{j(k)} ]
通過定義（使用非中心參數化）：

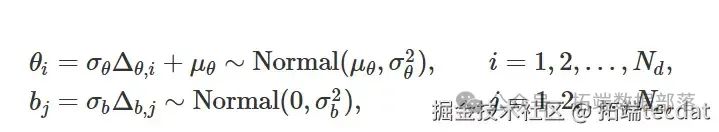
先驗/超先驗為：

PyMC實現

我們使用PyMC實現上述模型。為了方便跟蹤球員（因為我們有數百名犯規和被侵犯球員），我們使用pymc.Model的coords參數。以下是模型實現的代碼（AI提示詞：使用Python的PyMC庫實現上述定義的籃球犯規判罰的項目反應模型，設置好相關的先驗、超先驗、確定變量和似然等部分）：

我們繪制模型以顯示theta和b變量的層級結構（和非中心參數化）：

scss
代碼解讀
復制代碼
pm.model_to_graphviz(model)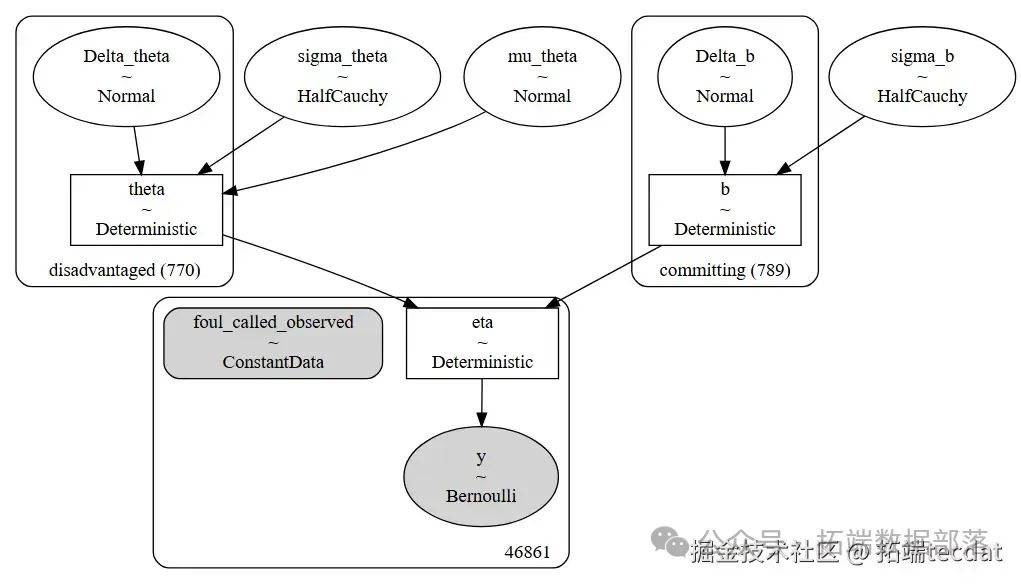

采樣與收斂

我們從拉施模型中進行采樣：

ini
代碼解讀
復制代碼
with model:
trace?= pm.sample(1000, tune=1500, random_seed=RANDOM_SEED)

我們繪制獲得的跟蹤的能量差異。同時，我們假設采樣器已經收斂，因為它通過了所有自動的PyMC收斂檢查：

ini
代碼解讀
復制代碼
az.plot_energy(trace);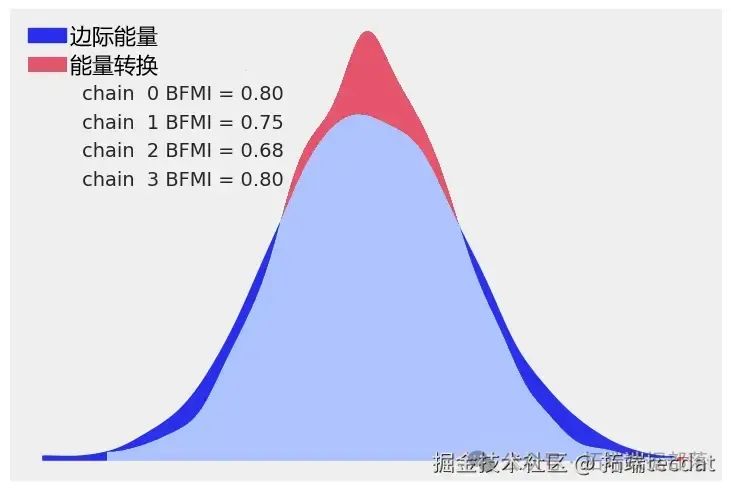

點擊標題查閱往期內容

Python貝葉斯MCMC：Metropolis-Hastings、Gibbs抽樣、分層模型、收斂性評估

左右滑動查看更多

后驗分析

部分池化的可視化

我們首先繪制每個被侵犯和犯規球員的原始平均概率（來自數據）與后驗平均概率之間的差異（(y)軸），以及每個被侵犯和犯規球員的觀察數量（(x)軸）。這些圖表明，正如預期的那樣，我們模型的層級結構傾向于將觀察數量較少的球員的后驗估計值拉向全局平均值。
以下是部分代碼（AI提示詞：使用Python的相關庫對后驗結果進行處理，計算原始平均概率與后驗平均概率的差異，并繪制差異與觀察數量的關系圖）：

ini
代碼解讀
復制代碼
# 全局后驗均值的μ_theta和μ_b
mu_theta_mean,?mu_b_mean?= trace.posterior["mu_theta"].mean(),?0
# 每個被侵犯球員的數據原始均值
disadvantaged_raw_mean?= df.groupby("disadvantaged")["foul_called"].mean()
# 每個犯規球員的數據原始均值
committing_raw_mean?= df.groupby("committing")["foul_called"].mean()
# 每個被侵犯球員的后驗均值
disadvantaged_posterior_mean?= (1 / (1 + np.exp(-trace.posterior["theta"].mean(dim=["chain",?"draw"]))).to_pandas()
)
# 每個犯規球員的后驗均值
committing_posterior_mean?= (1/ (1 + np.exp(-(mu_theta_mean - trace.posterior["b"].mean(dim=["chain",?"draw"])))).to_pandas()
)
# 計算每個被侵犯和犯規球員的原始和后驗均值的差異
def diff(a, b):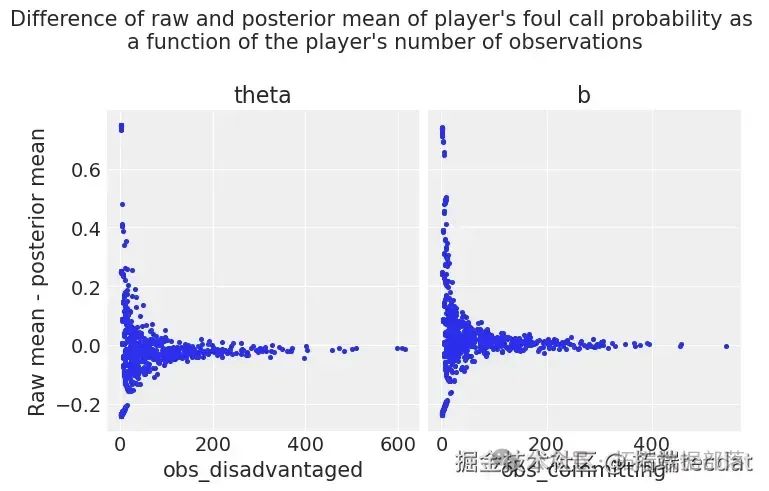

表現最佳和最差的犯規與被侵犯球員

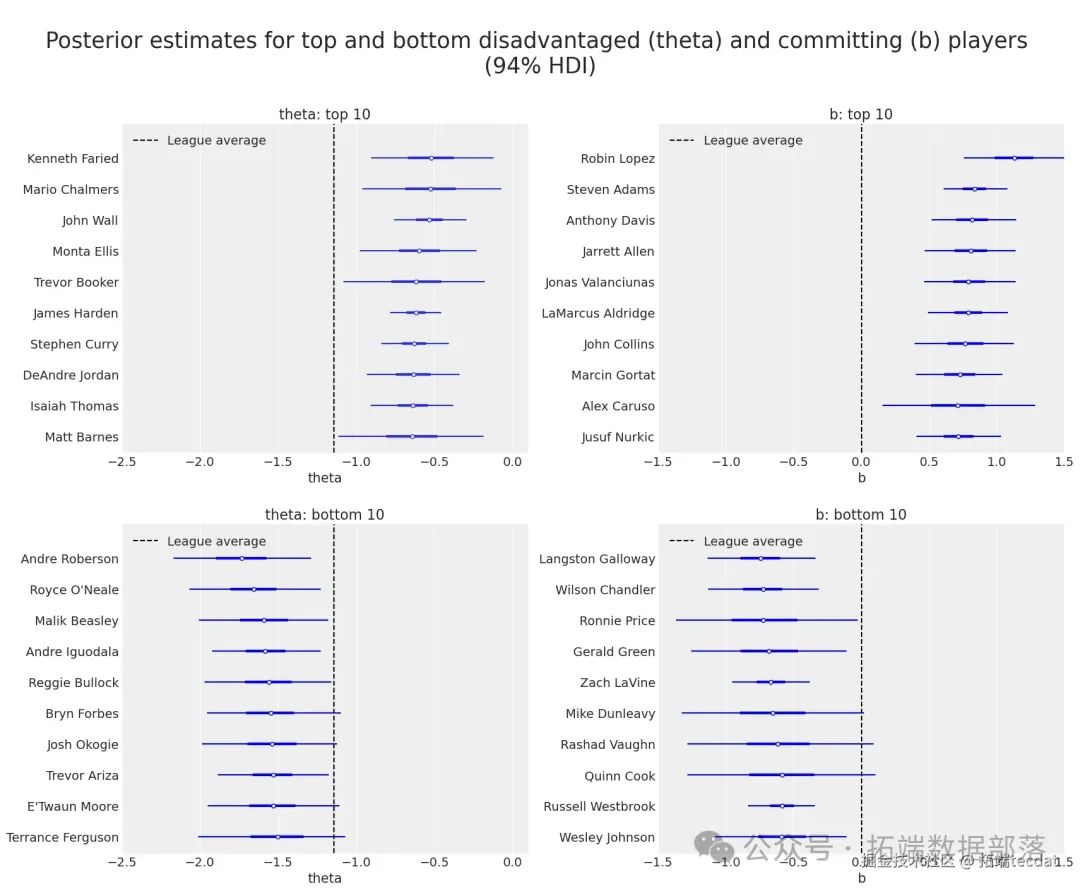
由于我們成功估計了被侵犯（theta）和犯規（b）球員的技能，我們可以檢查哪些球員在我們的模型中表現更好或更差。我們使用森林圖繪制后驗結果，分別繪制了在潛在技能theta和b方面排名前十和后十的球員。
以下是相關代碼（AI提示詞：使用Python的相關庫對后驗結果進行處理，根據潛在技能對球員進行排序，并繪制森林圖展示排名前十和后十的球員的后驗估計）：

ini
代碼解讀
復制代碼
def order_posterior(inferencedata, var, bottom_bool):
xarray_?= inferencedata.posterior[var].mean(dim=["chain",?"draw"])return xarray_.sortby(xarray_,?ascending=bottom_bool)
top_theta,?bottom_theta?= (order_posterior(trace, "theta", False),order_posterior(trace, "theta", True),
)
top_b,?bottom_b?= (order_posterior(trace,?"b",?False), order_posterior(trace,?"b",?True))
amount?=?10# 我們希望在每個類別中顯示的頂級球員數量

通過查看相關研究，并對比其中使用不同賽季數據的拉施模型結果表格，我們發現，在我們使用更大數據集（涵蓋2015 - 16到2020 - 21賽季）得到的模型中，一些在兩種技能（theta和b）上表現最佳的球員，仍然處于前十的排名。這表明我們的模型在不同數據規模下具有一定的穩定性和可靠性。

發現額外的層級結構

一個很自然的問題是，作為被侵犯球員表現出色（即theta值高）的球員，是否也有可能在作為犯規球員時同樣表現出色（即b值高），反之亦然。接下來的兩張圖展示了在b（或theta）方面表現最佳的球員的theta（或b）得分情況。

ini
代碼解讀
復制代碼
amount?=?20# 我們希望顯示的頂級球員數量
top_theta_players?= top_theta["disadvantaged"][:amount].values
top_b_players?= top_b["committing"][:amount].values
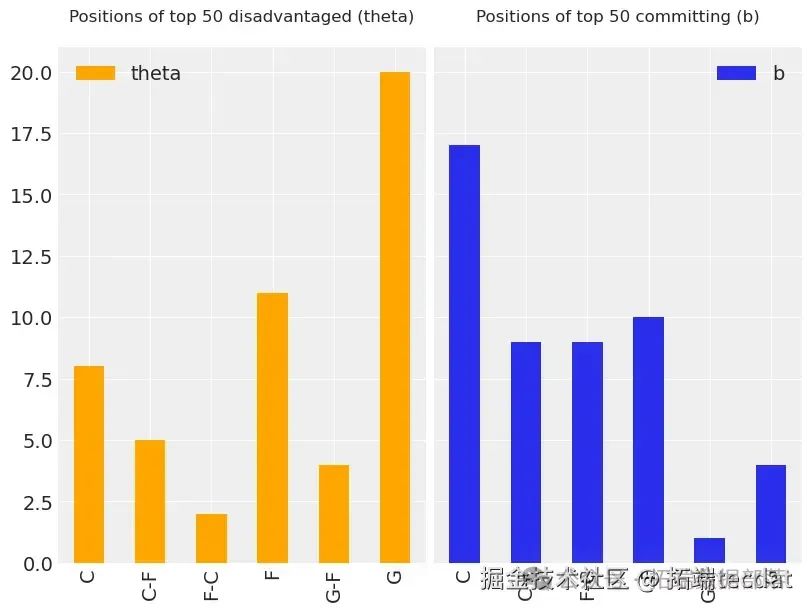
top_theta_in_committing?= set(committing).intersect

這些圖表明，theta得分高與b得分高或低之間沒有明顯的相關性。而且，對籃球稍有了解的人可以從圖中直觀地發現，中鋒或前鋒球員的b得分往往比后衛或控球后衛更高。基于這一觀察，我們決定繪制直方圖，展示在表現最佳的被侵犯（theta）和犯規（b）球員中，不同位置的出現頻率。

從直方圖中我們可以看到，表現最佳的被侵犯球員中，后衛占比最大；而表現最佳的犯規球員中，中鋒占比最大，同時后衛的占比非常小。這表明在我們的模型中，或許有必要添加一個層級結構。具體來說，可以按照球員的位置對被侵犯球員和犯規球員進行分組，以考慮位置因素在評估潛在技能theta和b時的作用。在拉施模型中，可以通過為按位置分組的每個球員設置均值和方差超先驗來實現這一點，感興趣的讀者可以自行嘗試。

結論

在本次研究中，我們運用貝葉斯項目反應理論對籃球犯規判罰數據進行了深入分析。通過構建拉施模型，結合實際數據，我們成功估計了球員在犯規和被侵犯情況下的潛在技能。
從數據收集與處理，到模型的定義、實現、采樣與收斂檢查，再到后驗結果的詳細分析，每一個環節都緊密相連。在分析過程中，我們不僅觀察到了模型中部分池化的效果，還通過對后驗結果的可視化，發現了球員表現與位置之間的潛在關系。
這一研究成果充分展示了貝葉斯建模在處理復雜層級結構數據時的強大能力和高度靈活性，它能夠幫助我們量化在引入特定問題知識時的不確定性。同時，本次研究也為后續進一步優化籃球犯規判罰分析模型提供了重要的思路和方向，例如考慮添加基于球員位置的層級結構等。未來，我們可以在此基礎上，繼續探索更多影響籃球犯規判罰的因素，不斷完善相關模型，為籃球比賽的分析和決策提供更有價值的參考。