PyTorch中的非線性激活函數詳解：原理、優缺點與實戰指南

在深度學習中，激活函數是神經網絡的核心組件之一，它決定了神經元的輸出是否被激活，并賦予網絡非線性建模能力。PyTorch提供了豐富的激活函數實現，本文將系統解析其數學原理、優缺點及適用場景，并給出實戰建議。

一、核心激活函數作用、分類與數學表達

PyTorch的激活函數可分為以下四類，每類包含典型代表及其數學形式：

作用：

1. 引入非線性：使網絡能夠學習復雜模式。
2. 特征映射：將輸入數據轉換到新的特征空間。
3. 梯度傳播控制：通過導數影響權重更新。

分類：

1. 飽和型（Sigmoid, Tanh）
2. ReLU族（ReLU, LeakyReLU, PReLU, ELU）
3. 自適應型（Swish, GELU, SELU）
4. 輕量型（ReLU6, Hardswish）

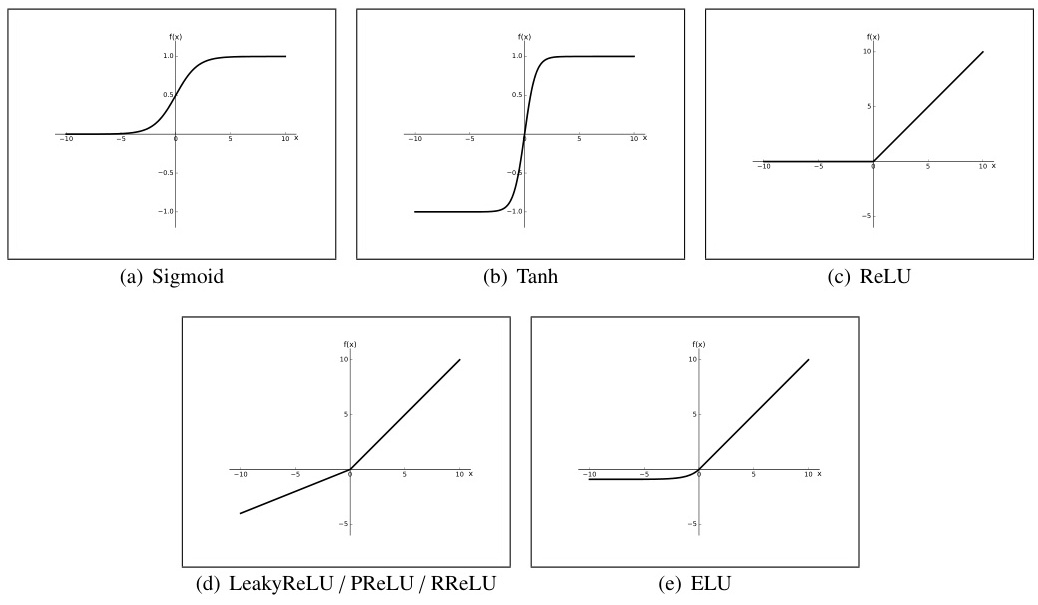
1. 傳統飽和型激活函數

• Sigmoid
  $\sigma (x)=\frac{1}{1+e^{?x}}$
  特點：輸出范圍(0,1)，適合二分類輸出層；缺點：梯度消失嚴重（導數最大僅0.25），輸出非零中心化。
  應用：二分類輸出層、LSTM門控。
• Tanh
  $\tanh (x)=\frac{e^x?e^{?x}}{e^x+e^{?x}}$
  特點：輸出范圍(-1,1)，零中心化；缺點：梯度消失問題仍存在（最大導數1.0），指數計算成本較高。
  應用：RNN隱藏層。

2. ReLU族（加權和類核心）

• ReLU
  $\text{ReLU}(x)=\max (0,x)$
  特點：計算高效，稀疏激活；缺點：負區間神經元死亡（Dead ReLU），輸出非零中心化。
  應用：CNN隱藏層（默認選擇）。
  

• Leaky ReLU
  $\text{LeakyReLU}(x)=\{\begin{array}{ll}x& x\ge 0\\ \alpha x& x<0\end{array}$
  特點：引入負區間斜率$\alpha$（通常0.01），緩解神經元死亡；缺點：需手動設定$\alpha$，性能提升有限。
  應用：替代ReLU的保守選擇。
  

• Parametric ReLU (PReLU)
  $\text{PReLU}(x)=\{\begin{array}{ll}x& x\ge 0\\ \alpha x& x<0\end{array}$（$\alpha$可學習）
  特點：自適應調整負區間斜率，適合復雜任務；缺點：增加參數量。

• Exponential Linear Unit (ELU)
  $\text{ELU}(x)=\{\begin{array}{ll}x& x\ge 0\\ \alpha (e^x?1)& x<0\end{array}$
  特點：負區間指數平滑，輸出接近零中心化；缺點：計算復雜度略高。
  應用：高魯棒性要求的深度網絡。

3. 自適應改進型激活函數

• Swish
  $\text{Swish}(x)=x?\sigma (\beta x)$（$\beta$可調）
  特點：平滑非單調，谷歌實驗顯示優于ReLU；缺點：計算量較大。
  應用：復雜任務（如NLP、GAN）。
• GELU
  $\text{GELU}(x)=x?\Phi (x)$（$\Phi (x)$為標準正態CDF）
  特點：引入隨機正則化思想（如Dropout），適合預訓練模型；缺點：近似計算需優化。
  應用：Transformer、BERT等預訓練模型。
• Self-Normalizing ELU (SELU)
  $\text{SELU}(x)=\lambda \{\begin{array}{ll}x& x\ge 0\\ \alpha (e^x?1)& x<0\end{array}$
  特點：自歸一化特性（零均值、單位方差），適合極深網絡；缺點：需配合特定初始化。
  應用：自編碼器、無監督學習。

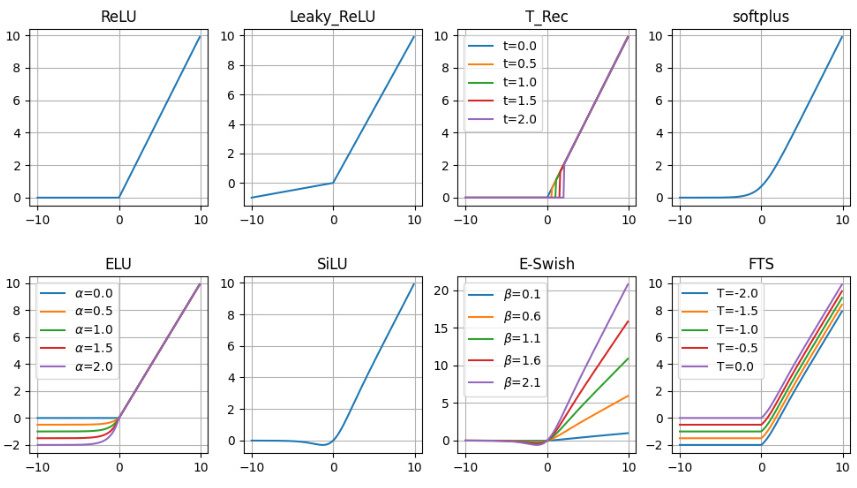
4. 輕量化與硬件友好型

• ReLU6
  $\text{ReLU6}(x)=\min (\max (0,x),6)$
  特點：限制正區間梯度，防止量化誤差（移動端模型）；缺點：犧牲部分表達能力。
  應用：移動端模型（如MobileNet）。
• Hardswish
  $\text{Hardswish}(x)=x?\frac{\min (\max (0,x+3),6)}{6}$
  特點：Swish的硬件優化版本，適合移動端；缺點：非線性較弱。
  應用：移動端實時推理。

---

二、優缺點對比與適用場景

激活函數	優點	缺點	適用場景
Sigmoid	輸出概率化，適合二分類輸出層	梯度消失嚴重，非零中心化	二分類輸出層，門控機制（如LSTM）
Tanh	零中心化，梯度略強于Sigmoid	梯度消失問題仍存在	RNN隱藏層
ReLU	計算高效，緩解梯度消失	神經元死亡，非零中心化	CNN隱藏層（默認選擇）
Leaky ReLU	緩解Dead ReLU問題	需手動調參，性能提升有限	替代ReLU的保守選擇
ELU	負區間平滑，噪聲魯棒性強	計算復雜度高	需要高魯棒性的深度網絡
Swish	平滑非單調，實驗性能優異	計算成本較高	復雜任務（如NLP、GAN）
GELU	結合隨機正則化，適合預訓練	需近似計算	Transformer、BERT類模型
SELU	自歸一化，適合極深網絡	依賴特定初始化（lecun_normal）	無監督/自編碼器結構
ReLU6	防止梯度爆炸，量化友好	表達能力受限	移動端部署（如MobileNet）

---

三、選擇策略與PyTorch實現建議

1. 隱藏層默認選擇：優先使用ReLU或改進版本（Leaky ReLU、ELU），平衡性能與計算成本。
2. 輸出層適配：
   • 二分類：Sigmoid
   • 多分類：Softmax（LogSoftmax配合NLLLoss更穩定）
   • 回歸任務：線性激活或Tanh（輸出范圍限制）
3. 極深網絡優化：使用SELU配合自歸一化初始化，或GELU增強非線性。
4. 移動端部署：選擇ReLU6或Hardswish，優化推理速度。
5. 實踐技巧：
   • 對Dead ReLU問題，可嘗試He初始化或加入BatchNorm。
   • 使用nn.Sequential時，注意激活函數的位置（通常在卷積/線性層后）。

---

四、PyTorch代碼示例

import torch.nn as nn# 定義含多種激活函數的網絡
class Net(nn.Module):def __init__(self):super().__init__()self.fc = nn.Linear(784, 256)self.act1 = nn.ReLU()        # 默認ReLUself.act2 = nn.LeakyReLU(0.01)  # Leaky ReLUself.act3 = nn.SELU()        # SELU（需配合lecun_normal初始化）def forward(self, x):x = self.fc(x)x = self.act1(x)x = self.act2(x)return self.act3(x)

---

五、選擇策略與實戰技巧

1. 隱藏層默認選擇：

   • 通用場景：優先使用ReLU，兼顧速度和性能。
   • 深度網絡：嘗試GELU或SELU（配合自歸一化初始化）。
   • 稀疏梯度需求：使用LeakyReLU或ELU。

2. 輸出層適配：

   • 二分類：Sigmoid（輸出概率）。
   • 多分類：Softmax（輸出概率分布）。
   • 回歸任務：無激活（線性輸出）或Tanh（限制范圍）。

3. 避免Dead ReLU：

   • 使用He初始化（init.kaiming_normal_）。
   • 加入Batch Normalization層。
   • 設置適當的學習率（過大易導致神經元死亡）。

4. 移動端優化：

   • 選擇ReLU6或Hardswish，減少浮點運算。
   • 使用PyTorch的量化工具鏈（如TorchScript）。

5. 代碼示例：

   import torch.nn as nn
   import torch.nn.init as initclass DeepNetwork(nn.Module):def __init__(self):super().__init__()self.fc1 = nn.Linear(784, 256)self.act1 = nn.GELU()         # 使用GELUself.fc2 = nn.Linear(256, 128)self.act2 = nn.SELU()         # 使用SELU需配合特定初始化self._init_weights()def _init_weights(self):init.kaiming_normal_(self.fc1.weight, nonlinearity='gelu')init.lecun_normal_(self.fc2.weight)  # SELU推薦初始化def forward(self, x):x = self.act1(self.fc1(x))x = self.act2(self.fc2(x))return x
   

---

六、總結

• ReLU族仍是隱藏層的首選，平衡速度與性能。
• GELU/Swish在復雜任務中表現優異，但需權衡計算成本。
• SELU在極深網絡中潛力大，但依賴嚴格初始化。
• 輕量型函數（如Hardswish）是移動端部署的關鍵。

實際應用中，建議通過實驗（如交叉驗證）選擇最佳激活函數，并結合模型結構、數據分布和硬件條件綜合優化。