4.3 數值微分

梯度法使用梯度的信息決定前進的方向。本節將介紹梯度是什么、有什么性質等內容。

4.3.1 導數

假如你是全程馬拉松選手，在開始的10分鐘內跑了2千米。如果要計算此時的奔跑速度，則為2/10 = 0.2［千米/分］。也就是說，你以1分鐘前進0.2千米的速度（變化）奔跑。

在這個馬拉松的例子中，我們計算了“奔跑的距離”相對于“時間”發生了多大變化。不過，這個10分鐘跑2千米的計算方式，嚴格地講，計算的是10分鐘內的平均速度。而導數表示的是某個瞬間的變化量。因此，將10分鐘這一時間段盡可能地縮短，比如計算前1分鐘奔跑的距離、前1秒鐘奔跑的距離、前0.1秒鐘奔跑的距離……這樣就可以獲得某個瞬間的變化量（某個瞬時速度）。

綜上，導數就是表示某個瞬間的變化量。它可以定義成下面的式子。

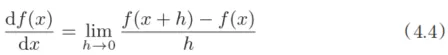
式（4.4）表示的是函數的導數。左邊的符號

表示f（x）關于x的導數，即f（x）相對于x的變化程度。式（4.4）表示的導數的含義是，x的“微小變化”將導致函數f（x）的值在多大程度上發生變化。

如果直接實現式（4.4）的話，向h中賦入一個微小值，就可以計算出來了。比如，下面的實現如何？

函數numerical_diff(f, x)的名稱來源于數值微分A 的英文numerical differentiation。這個函數有兩個參數，即“函數f”和“傳給函數f的參數x”。乍一看這個實現沒有問題，但是實際上這段代碼有兩處需要改進的地方。

如上所示，如果用float32類型（32位的浮點數）來表示1e-50，就會變成0.0，無法正確表示出來。也就是說，使用過小的值會造成計算機出現計算上的問題。這是第一個需要改進的地方，即將微小值h改為

。使用

就可以得到正確的結果。

第二個需要改進的地方與函數f的差分有關。雖然上述實現中計算了函數f在x+h和x之間的差分，但是必須注意到，這個計算從一開始就有誤差。如圖4-5所示，“真的導數”對應函數在x處的斜率（稱為切線），但上述實現中計算的導數對應的是(x + h)和x之間的斜率。因此，真的導數（真的切線）和上述實現中得到的導數的值在嚴格意義上并不一致。這個差異的出現是因為h不可能無限接近0。

數值微分含有誤差。為了減小這個誤差，我們可以計算函數f在(x + h)和(x ? h)之間的差分。因為這種計算方法以x為中心，計算它左右兩邊的差分，所以也稱為中心差分（而(x + h)和x之間的差分稱為前向差分）

讓我們用一個簡單的類比來理解：

想象你開車，想知道在下午3:00整這一瞬間的瞬時速度（這就是“真的導數”）

方法A（前向差分）：你記錄下3:00的里程表讀數，然后開到3:01再記錄一次讀數，用里程差除以1分鐘。你得到的是3:00到3:01這1分鐘內的平均速度，而不是3:00整的瞬時速度。這個平均速度可能接近，但絕不等于瞬時速度。

方法B（中心差分）：你記錄下2:59的里程表讀數，然后開到3:01再記錄一次讀數，用里程差除以2分鐘。你得到的是2:59到3:01這2分鐘內的平均速度，而這個平均速度的中心點正好是3:00。由于你的速度不太可能在這2分鐘內劇烈波動，這個以3:00為中心的平均速度，通常會比方法A得到的那個從3:00開始的平均速度，更能準確地反映3:00整的瞬時速度。

函數定義如下

4.3.2 數值微分的例子

現在我們試著用上述的數值微分對簡單函數進行求導。先來看一個由下式表示的2次函數。

用Python來實現式（4.5），如下所示。

接下來，我們來繪制這個函數的圖像。畫圖所用的代碼如下

圖像如下

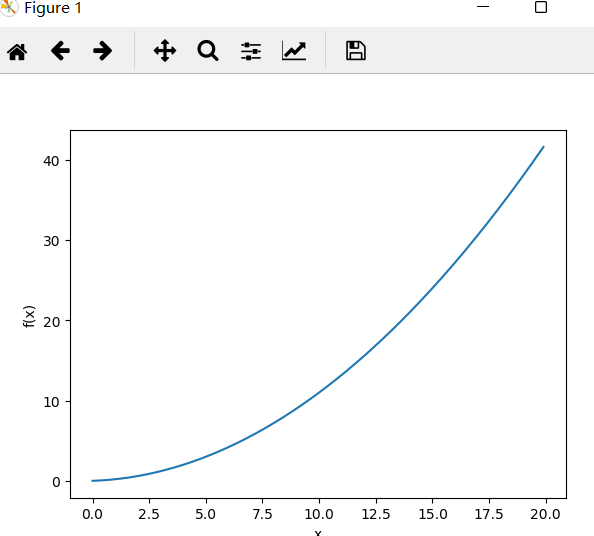
我們來計算一下這個函數在x = 5和x = 10處的導數。

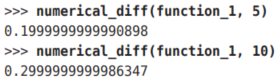
這里計算的導數是f(x)相對于x的變化量，對應函數的斜率。另外，f(x) = 0.01x2 + 0.1x 的解析解是

。因 此，在 x = 5 和x = 10處，“真的導數”分別為0.2和0.3。和上面的結果相比，我們發現雖然嚴格意義上它們并不一致，但誤差非常小。實際上，誤差小到基本上可以認為它們是相等的。

4.3.3 偏導數

接下來，我們看一下式(4.6)表示的函數。雖然它只是一個計算參數的平方和的簡單函數，但是請注意和上例不同的是，這里有兩個變量。

這個式子可以用Python來實現，如下所示。

這里，我們假定向參數輸入了一個NumPy數組。函數的內部實現比較簡單，先計算NumPy數組中各個元素的平方，再求它們的和（np.sum(x**2)也可以實現同樣的處理）。我們來畫一下這個函數的圖像。結果如圖4-8所示，是一個三維圖像。

現在我們來求式（4.6）的導數。這里需要注意的是，式（4.6）有兩個變量，所以有必要區分對哪個變量求導數，即對x0和x1兩個變量中的哪一個求導數。另外，我們把這里討論的有多個變量的函數的導數稱為偏導數。用數學式表示的話，可以寫成

怎么求偏導數呢？我們先試著解一下下面兩個關于偏導數的問題。

問題1：求x0 = 3, x1 = 4時，關于x0的偏導數

問題2：求x0 = 3, x1 = 4時，關于x1的偏導數

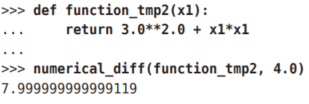
在這些問題中，我們定義了一個只有一個變量的函數，并對這個函數進行了求導。例如，問題1中，我們定義了一個固定x1 = 4的新函數，然后對只有變量x0的函數應用了求數值微分的函數。從上面的計算結果可知，問題1的答案是6.00000000000378，問題2的答案是7.999999999999119，和解析解的導數基本一致。

像這樣，偏導數和單變量的導數一樣，都是求某個地方的斜率。不過，偏導數需要將多個變量中的某一個變量定為目標變量，并將其他變量固定為某個值。

在上例的代碼中，為了將目標變量以外的變量固定到某些特定的值上，我們定義了新函數。然后，對新定義的函數應用了之前的求數值微分的函數，得到偏導數。