一、核心基礎概念
- 核心目標:在樣本空間中找到劃分超平面,將不同類別樣本分開,且該超平面對訓練樣本局部擾動的 “容忍性” 最優(即抗干擾能力強)。
- 超平面定義
- 超平面是 n 維空間中的 n-1 維子空間,是 SVM 分類的核心依據:
- 3 維空間中,超平面為 2 維平面;2 維空間中,超平面為 1 維直線。
- 數學表達式:wTx+b=0,其中w是 n 維向量(超平面法向量),b是實數(超平面截距),x是樣本向量。
- 超平面是 n 維空間中的 n-1 維子空間,是 SVM 分類的核心依據:
- 關鍵指標:Margin(間隔)與支持向量
- Margin(間隔):兩類樣本中距離超平面最近的點到超平面距離的 2 倍(Margin=2d,d為最近點到超平面的距離),SVM 的核心優化目標是最大化 Margin,以提升模型泛化能力。
- 支持向量:距離超平面最近的樣本點,是決定超平面位置的關鍵樣本,其他樣本對超平面無影響。
- 樣本標簽與決策方程
- 樣本標簽:正例標注為y=+1,負例標注為y=?1,便于后續約束條件推導。
- 決策方程:y(x)=w?Φ(x)+b,其中Φ(x)是樣本x的特征映射(用于解決低維不可分問題,后續詳細說明),若y(x)>0預測為正例,y(x)<0預測為負例。
二、核心優化邏輯
(一)優化目標推導
- 初始目標:最大化間隔Margin=2d,等價于最大化單個最近點到超平面的距離d。
- 點到超平面距離公式:n 維空間中,樣本x到超平面wTx+b=0的距離為d=wTw?∣wTx+b∣?。
- 約束條件簡化:通過對w和b進行放縮變換,使所有樣本滿足yi??(w?Φ(xi?)+b)≥1(保證所有樣本在超平面 “正確一側”,且支持向量滿足等號yi??(w?Φ(xi?)+b)=1)。
- 目標函數轉換:最大化d=wTw?1?(由距離公式及約束條件推導),等價于最小化21?wTw(將極大值問題轉化為更易求解的極小值問題,且平方項可簡化計算)。
(二)帶約束優化求解:拉格朗日乘子法
- 優化問題形式
- 目標函數(極小化):minw,b?21?wTw
- 約束條件(不等式):yi??(w?Φ(xi?)+b)≥1(i=1,2,...,n,n為樣本數)
- 拉格朗日函數構建:引入拉格朗日乘子αi?≥0,將帶約束優化轉化為無約束優化,函數形式為:L(w,b,α)=21?wTw?∑i=1n?αi?[yi??(w?Φ(xi?)+b)?1]
- 求解關鍵條件:對w和b求偏導并令其等于 0,得到核心等式:
- w=∑i=1n?αi?yi?Φ(xi?)(w由支持向量的αi?、yi?和Φ(xi?)決定)
- ∑i=1n?αi?yi?=0(αi?的約束條件)
- 對偶問題轉化:將w的表達式代入拉格朗日函數,原問題轉化為對偶問題 ——最大化∑i=1n?αi??21?∑i=1n?∑j=1n?αi?αj?yi?yj?Φ(xi?)TΦ(xj?),約束條件為∑i=1n?αi?yi?=0且αi?≥0。
三、關鍵拓展:解決實際問題
(一)軟間隔:應對噪聲與非完全可分數據
- 問題背景:現實數據常存在噪聲,硬間隔(要求所有樣本滿足yi??(w?Φ(xi?)+b)≥1)會導致超平面劃分效果差。
- 解決方案:引入松弛因子ξi?
- 調整約束條件:yi??(w?Φ(xi?)+b)≥1?ξi?(ξi?≥0,ξi?越大,允許樣本偏離 “理想位置” 越多)。
- 調整目標函數:minw,b,ξ?21?wTw+C∑i=1n?ξi?,其中C是懲罰參數:
- C趨近于極大值:懲罰強,不允許樣本偏離,等價于硬間隔。
- C趨近于極小值:懲罰弱,允許更多樣本偏離,避免過擬合。
- 軟間隔對偶求解:約束條件變為0≤αi?≤C(原硬間隔αi?≥0),其余求解邏輯與硬間隔一致。
(二)核變換:解決低維不可分問題
- 問題背景:部分數據在低維空間中無法用線性超平面分離(如環形分布數據)。
- 核心思路:通過特征映射Φ(x)將低維輸入空間的樣本映射到高維特征空間,使數據在高維空間中線性可分。
- 核函數:避免高維計算災難
- 問題:高維空間中計算Φ(xi?)TΦ(xj?)(內積)復雜度極高(如 3 維映射到 9 維,復雜度為O(n2))。
- 解決方案:引入核函數K(xi?,xj?)=Φ(xi?)TΦ(xj?),直接在低維空間計算,等價于高維空間內積,降低計算成本。
- 常見核函數
- 線性核函數:適用于線性可分數據,K(xi?,xj?)=xiT?xj?。
- 高斯核函數(RBF 核):適用于非線性可分數據,能將數據映射到無限維空間,K(xi?,xj?)=exp(?2σ2∥xi??xj?∥2?)(σ為帶寬參數,影響核函數平滑度)。
四、總結
支持向量機以 “最大化間隔” 為核心優化目標,通過硬間隔(線性可分)、軟間隔(應對噪聲)、核變換(應對非線性)三大策略,適配不同數據場景;求解過程依賴拉格朗日乘子法與對偶問題轉化,最終僅通過支持向量即可確定超平面,具備模型簡潔、泛化能力強的優勢,是分類任務中的經典且高效算法。
五、代碼
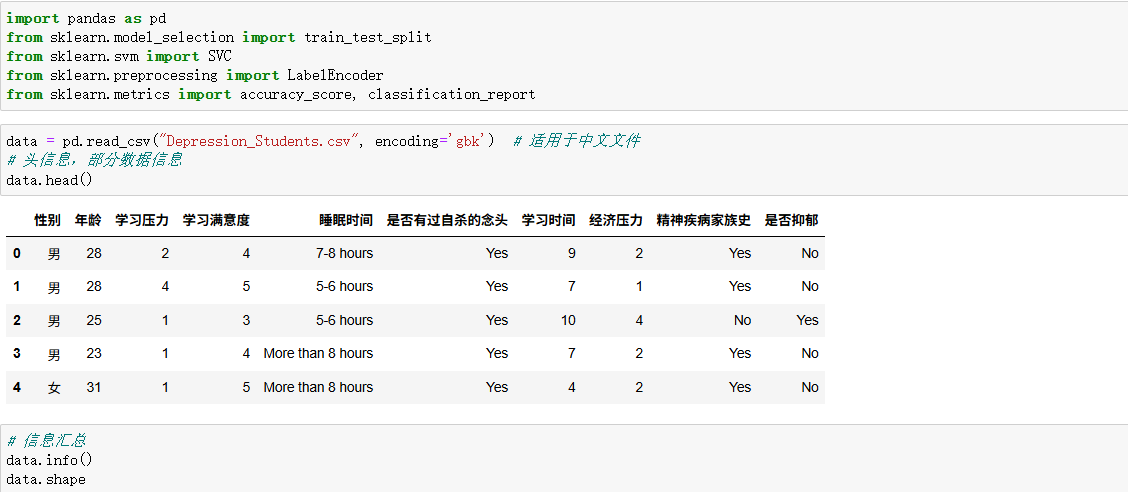
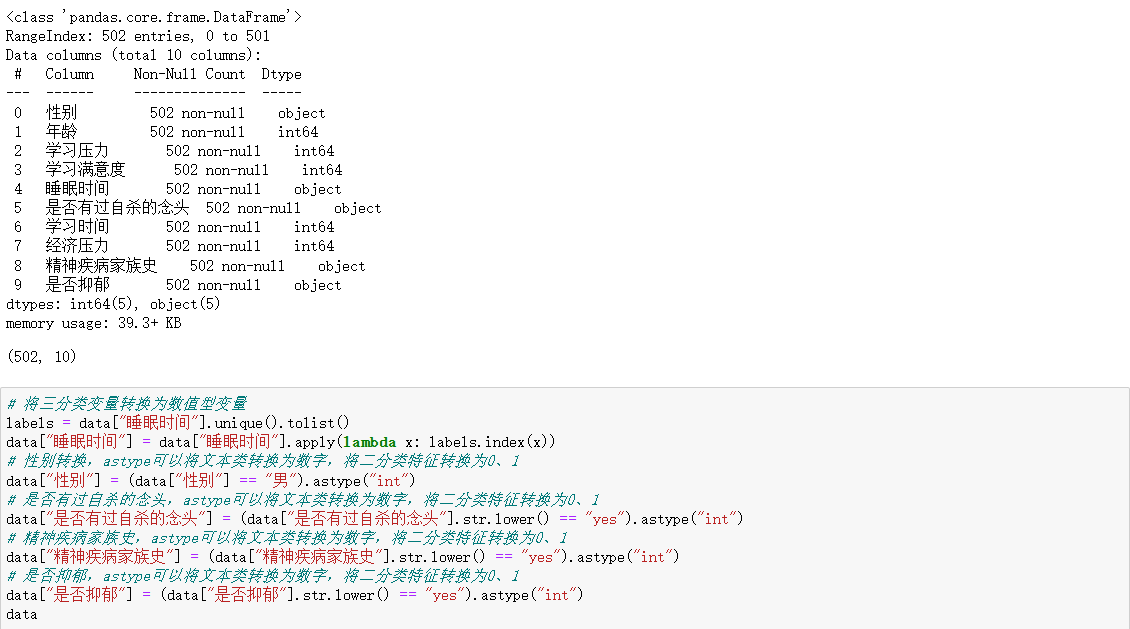
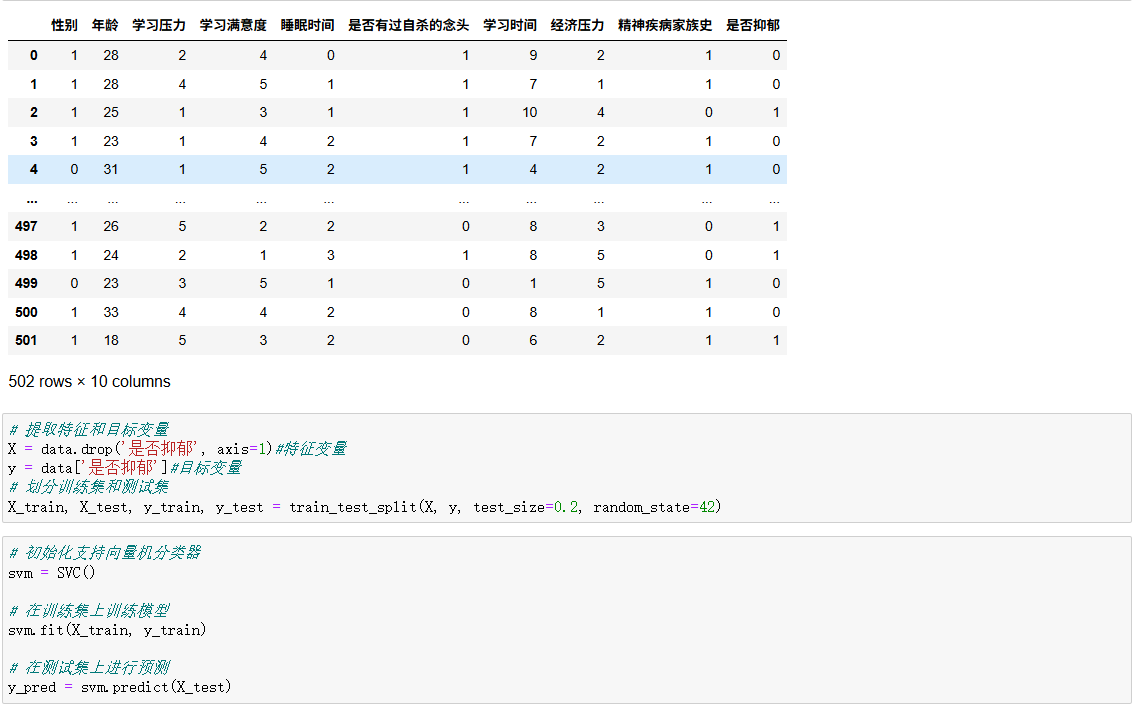
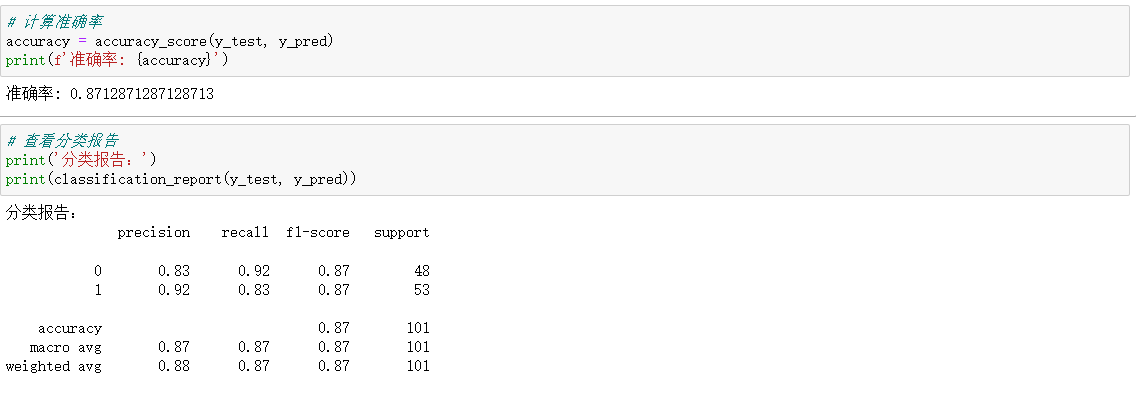







)



)

(MatlabPython代碼實現))

(pgAdmin內置、DBeaver、Azure Data Studio)數據庫命令行工具)



)