這是封面原圖，嘿嘿：

二分查找：從基礎原理到代碼實現

二分查找，這個在算法世界里算不上復雜卻總讓人在細節上栽跟頭的算法，估計不少人都有過類似經歷——明明原理一聽就懂，上手寫卻總寫出死循環，要么就是邊界條件處理得一塌糊涂。但只要真正摸透了它的規律，就會發現它其實是個“只要學會就簡單”的典型，今天咱們就借著LeetCode 704.二分查找這道基礎題，把它的來龍去脈說清楚。

二分查找的特點

為啥二分查找總讓人覺得“看著簡單寫著難”？

其實核心就是細節太多：
比如這些極易混淆的關鍵問題，稍不注意就會出錯：

• 左邊界是left還是left+1？
• 右邊界該初始化成nums.size()還是nums.size()-1？
• 循環條件用left < right還是left <= right？

這些小地方一旦疏忽，要么陷入死循環，要么出現漏查元素，甚至引發越界訪問，堪稱二分查找的“坑點重災區”。

但它的優點也同樣突出，尤其是在效率上的碾壓性優勢：

• 時間復雜度：O(log n)，對比暴力遍歷的O(n)，在數據量大時效率天差地別。

舉個直觀的例子：
要在100萬個元素中查找一個目標數：

• 暴力遍歷：最壞情況下需要查100萬次；
• 二分查找：最壞情況下僅需20次（因為2^20≈100萬）。

這也是二分查找能成為面試高頻考點的核心原因。

算法重點

1.原理：不只是“有序”，更是“二段性”

「??核心」我們在剛開始接觸二分查找的時候經常聽說二分查找必須是數組有序的時候才能使用，其實這樣說會有些片面，其中本質不是“有序”，而是數組具有 “二段性”
至于什么是二段性簡單說就是：能找到一個 “判斷條件”，把數組分成兩部分 ，一部分一定滿足條件，另一部分一定不滿足，這樣就說這個數組具有二段性

「??類比」 比如在書架上找一本《Python編程》，書架是按書名首字母排序的。你隨便抽一本中間的書，比如《Java編程》（首字母J），發現它在P的左邊，那你就知道《Python編程》一定在右邊——這就是生活中的“二段性”。

回到這道題，數組是升序的，“判斷條件”就可以是“元素是否小于target”：左邊的元素都小于target，右邊的元素都大于等于target（或者反過來）。正是因為有了這種“二段性”，我們才能每次拿中間元素和target比，然后果斷排除左邊或右邊的一半，不用逐個遍歷。

2.模板：理解邏輯比死記代碼重要

二分查找確實有成熟的“模板”，但千萬別死記硬背——就像手里握著卡塞爾裝備部遞來的屠龍武器，卻忘了如何激活、如何瞄準，那這把武器反而不如一把普通匕首實用（龍族亂入嘿嘿）。

常見的二分查找模板主要分為以下三種，適用場景各有不同：

模板類型	核心適用場景	特點
樸素二分查找	查找“唯一存在的目標元素”	邏輯最簡單，上手快，但局限性強，僅適用于元素無重復的場景（本文題目使用的就是該模板）
查找左邊界	查找“目標元素第一次出現的位置”	適用性更廣，能處理元素重復的情況，細節點更多（如邊界收縮邏輯）
查找右邊界	查找“目標元素最后一次出現的位置”	與左邊界模板邏輯互補，同樣適用于重復元素場景，是解決復雜查找問題的常用工具

其中，后兩種模板（左邊界、右邊界查找）功能性更萬能，但涉及的邊界處理、循環終止條件等細節也更復雜。咱們明天拆解LeetCode 34題（在排序數組中查找元素的第一個和最后一個位置）時，再逐行梳理這兩種模板的邏輯；今天的重點，是通過LeetCode 704題先把最基礎的“樸素二分查找”徹底吃透，打好根基。

題目描述：LeetCode 704. 二分查找

題目鏈接：二分查找

題目描述：

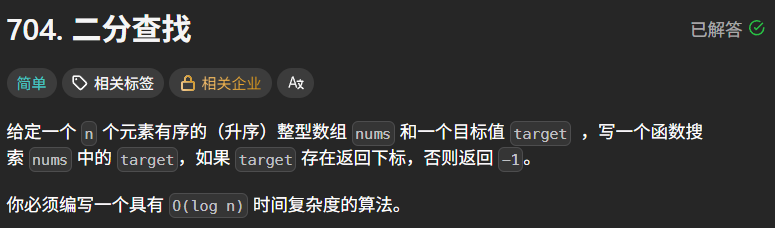
示例 1:
輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中并且下標為 4

示例 2:
輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

提示：
1.你可以假設 nums 中的所有元素是不重復的。
2.n 將在 [1, 10000]之間。
3.nums 的每個元素都將在 [-9999, 9999]之間。

為什么可以用二分查找？

在討論二分查找時，我們不僅要知道“能用”，更要想清楚“為什么用”，以及“遇到隨機題目時怎么和二分關聯”——這才是掌握算法的關鍵 ?

我們先看“為什么可以用”：二分查找的核心是利用“二段性”縮小范圍，而這道題恰好完美契合這個前提→題目中的數組是升序排列的。

假設我們隨便選數組中間的元素 nums[mid]，和目標值 target 對比，會立刻出現三種清晰的情況，每一種都能幫我們“砍掉”一半無用的查找范圍 🪓：

1. 若 nums[mid] == target 🎯：直接命中答案！不需要再找了，直接返回 mid 即可；
2. 若 nums[mid] > target 📈：因為數組是升序的，mid 右邊所有元素都會比 nums[mid] 更大，自然也比 target 大——這半邊完全不用看了，下次只查 mid 左邊；
3. 若 nums[mid] < target 📉：同理，mid 左邊所有元素都會比 nums[mid] 更小，自然也比 target 小——這半邊可以直接舍棄，下次只查 mid 右邊。

之前提到的“二段性”，在這里也直接體現出來我們通過 mid 和 target 的大小關系，我們能把數組精準分成兩部分——一部分是有用的查找范圍，另一部分是可以直接扔掉的無效范圍。

正因為每次都能把查找范圍縮小到原來的 1/2，二分查找才能實現 O(log n) 的高效時間復雜度，這也是它比暴力遍歷（O(n)）強的根本原因 💪

暴力算法解法

既然題目要求O(log n)，那肯定不能用暴力，但咱們還是先說說暴力解法，對比一下就能更直觀感受到二分的優勢。

暴力解法很簡單：從頭到尾遍歷數組，逐個比較元素和target。如果找到相等的，就返回下標；遍歷完都沒找到，就返回-1。代碼大概長這樣：

int search(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); i++) {if (nums[i] == target) {return i;}}return -1;
}

這代碼肯定能跑通，但時間復雜度是O(n)——如果數組有10000個元素，最壞情況要循環10000次。現在對兩個方法的時間復雜度沒有太多概念沒有關系，后面我們會詳細說到

二分查找解法

核心邏輯：三種情況的處理

剛才其實已經說了核心思路：每次取中間元素mid，和target比，然后根據結果縮小范圍。具體來說：

1. 初始化左右邊界：left = 0，right = nums.size() - 1（因為數組下標從0開始，最后一個元素下標是size-1）
2. 循環查找：只要left <= right就證明再合法范圍內（注意這里是“<=”，后面說原因），在這個區間才能繼續計算中間下標mid
3. 比較nums[mid]和target：
   • nums[mid] = target：找到目標，記錄下標，跳出循環；
   • nums[mid] > target：說明目標在左邊，把右邊界移到mid - 1（因為mid已經查過了，不用再考慮）
   • nums[mid] < target：說明目標在右邊，把左邊界移到mid + 1（同理，mid不用再考慮）
4. 如果循環結束都沒找到，返回-1。

二分查找什么時候結束？

可能有人會想：為什么循環條件不能用left < right？
比如數組只剩一個元素時，left和right相等，這時候left < right不成立，循環就結束了，那這個元素不就漏查了嗎？

比如數組[5]，target是5：初始left=0，right=0，left <= right成立，進去計算mid=0，發現nums[mid]==target，返回0——正確。

如果target是3，數組還是[5]：第一次循環mid=0，nums[mid] > target，所以right=mid-1=-1。這時候left=0，right=-1，left > right，循環結束，返回-1——也正確。

為什么二分查找一定是對的？

這道題中，我們可以明確數組是嚴格升序排列的，單調性極其明確——正是這個特性，為二分查找“安全縮小范圍”提供了根本保障。

只要數組滿足單調性（升序或降序），通過“中間元素 nums[mid] 與 target 的大小對比”，就能精準劃分“有效范圍”與“無效范圍”，絕不會出現“漏查目標”的情況：

• 若數組升序：nums[mid] > target → 右半區所有元素均 > target（無效，可舍棄）；nums[mid] < target → 左半區所有元素均 < target（無效，可舍棄）；
• 若數組降序：邏輯相反，但同樣能通過一次對比砍掉一半范圍。

這種“每次縮小范圍都絕對安全”的特性，讓二分查找最終要么精準定位到目標（若存在），要么確定目標不存在——不會出現“范圍縮錯導致漏查”的問題。

數學證明：單調性下二分查找的有效性（數學歸納法）

證明目標：對于非空有序數組 nums（此處以升序為例），若 target 在 nums 中，則二分查找必能找到；若不在，則必能判斷不存在。

1. 基礎情況（n=1，數組僅1個元素）

• 若 nums[0] == target：直接返回下標0，找到目標；
• 若 nums[0] != target：循環結束，判斷目標不存在。
  基礎情況成立。

2. 歸納假設（假設數組長度為k時，結論成立）
即：對于長度為k的升序數組 nums，二分查找能正確判斷 target 是否存在（存在則返回下標，不存在則返回不存在）。

3. 歸納遞推（證明數組長度為k+1時，結論仍成立）
對于長度為k+1的升序數組 nums，取中間下標 mid = left + (right - left) // 2（避免溢出），對比 nums[mid] 與 target：

• 情況1：nums[mid] == target：直接返回mid，找到目標，結論成立；
• 情況2：nums[mid] > target：因數組升序，mid 右側（共 (k+1)-mid-1 ≤ k 個元素）均 > target，可舍棄，剩余查找范圍為 [left, mid-1]（長度 ≤k）。根據歸納假設，對長度≤k的數組，二分查找能正確判斷，故結論成立；
• 情況3：nums[mid] < target：因數組升序，mid 左側（共 mid - left ≤ k 個元素）均 < target，可舍棄，剩余查找范圍為 [mid+1, right]（長度 ≤k）。同理，根據歸納假設，結論成立。

綜上，當數組長度為k+1時，結論仍成立。

由數學歸納法可知，對任意長度的有序數組，二分查找的有效性均成立——這也是“單調性”為二分查找提供的數學層面的保障。

時間復雜度

二分查找的核心優勢在于每次將查找范圍縮小為原來的 1/2，這個“減半”過程直到范圍為空或找到目標才停止。我們可以通過“查找次數”與“初始范圍大小”的對應關系，直觀看到時間復雜度為何是 O(log n)。

假設初始查找范圍包含 n 個元素，每次縮小后范圍大小如下表所示（“第k次查找后”指完成第k輪對比與范圍調整后的剩余元素數）：

查找輪次	剩余查找范圍大小	對應關系（以2的冪次表示）
初始狀態	n	n = 2^log?n
第1次后	n/2	n/2 = 2^(log?n - 1)
第2次后	n/4	n/4 = 2^(log?n - 2)
第3次后	n/8	n/8 = 2^(log?n - 3)
…	…	…
第k次后	n/(2^k)	n/(2^k) = 2^(log?n - k)
終止時	≤1	n/(2^k) ≤ 1 → 2^k ≥ n

當查找終止時，剩余范圍大小 ≤1（要么找到目標，要么確認目標不存在），此時滿足：
n/(2^k) ≤ 1
對不等式變形可得：
2^k ≥ n
兩邊取以2為底的對數（log?），根據對數單調性，不等號方向不變：
k ≥ log?n
由于查找次數 k 必須是整數，因此最多需要 ?log?n? 次查找（?x? 表示向上取整，如 log?100萬≈19.93，向上取整為20次）。

舉個直觀例子： 👇

• 當 n=100萬時，log?100萬≈19.93 → 最多只需20次查找；
• 當 n=10億時，log?10億≈29.89 → 最多只需30次查找。
  這就是“對數級復雜度”在數據量大時的壓倒性優勢。

代碼

下面是我寫的代碼，結合注釋咱們再捋一遍細節：

class Solution {
public:int search(vector<int>& nums, int target) {// 初始化左邊界為0，右邊界為數組最后一個元素的下標int right = nums.size() - 1, left = 0;// 用于記錄結果，默認-1（沒找到）int ret = -1;// 循環條件：left <= right（確保所有可能的位置都查過）while (left <= right) {  // 🌟 閉區間循環條件！別漏了"="// 計算中間下標：用left + (right - left)/2代替(left+right)/2，避免溢出int middle = left + (right - left) / 2;  // 🌟 防溢出！別寫成(right+left)/2// 如果中間元素等于target，找到目標，記錄下標并跳出循環if (nums[middle] == target) {ret = middle;break;}// 如果中間元素大于target，說明目標在左邊，右邊界左移到middle-1else if (nums[middle] > target) {right = middle - 1;}// 如果中間元素小于target，說明目標在右邊，左邊界右移到middle+1else {left = middle + 1;}}return ret;}
};

這里有個細節必須提：計算middle的時候，為什么用left + (right - left)/2而不是(left + right)/2？

📌 記住：計算mid永遠用 left + (right - left)/2，不用(right+left)/2！兩者數學結果相同，但前者能避免left和right過大時的整數溢出（比如 left=2^30 ，right=2^30時，right+left會超INT_MAX）。

為什么是二分不是三分、四分？

有人可能會想：既然二分能縮小一半范圍，那三分、四分是不是更快？理論上每次縮小更多范圍，次數應該更少？

其實不一定。咱們先寫個三分查找的例子感受下：

// 三分查找示例（針對升序數組找target）
int ternarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {// 把范圍分成三份，找兩個中間點int mid1 = left + (right - left) / 3;int mid2 = right - (right - left) / 3;if (nums[mid1] == target) return mid1;if (nums[mid2] == target) return mid2;// 根據target位置縮小范圍if (target < nums[mid1]) {right = mid1 - 1;} else if (target > nums[mid2]) {left = mid2 + 1;} else {left = mid1 + 1;right = mid2 - 1;}}return -1;
}

四分查找原理類似，就是分的段更多，中間點更多。

但為什么實際中幾乎沒人用三分、四分？因為：

• 時間復雜度差距不大：二分是O(log?n)，三分是O(log?n)，四分是O(log?n)。但log?n ≈ 1.58log?n ≈ 2log?n，差距很小。比如n=1e6，二分要20次，三分只要12次，四分只要10次——次數少了，但每次循環里的操作變多了（三分要算兩個中間點，判斷兩次）；
• 代碼復雜度上升：分的段越多，邊界條件越復雜，越容易出錯，維護成本高，而且一點選錯成本會更高；
• 實際效率未必更高：雖然次數少，但每次循環的計算、判斷步驟多，整體耗時可能反而比二分更長。

咱們可以寫個簡單的程序測試下（用隨機數組+多次查找計時）：

#include <iostream>
#include <vector>
#include <random>
#include <chrono>using namespace std;// 二分查找
int binarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}return -1;
}// 三分查找
int ternarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid1 = left + (right - left) / 3;int mid2 = right - (right - left) / 3;if (nums[mid1] == target) return mid1;if (nums[mid2] == target) return mid2;if (target < nums[mid1]) right = mid1 - 1;else if (target > nums[mid2]) left = mid2 + 1;else {left = mid1 + 1;right = mid2 - 1;}}return -1;
}int main() {// 生成一個100萬個元素的升序數組int n = 1000000;vector<int> nums(n);for (int i = 0; i < n; i++) {nums[i] = i;}// 隨機生成1000個目標值（確保在數組范圍內）random_device rd;mt19937 gen(rd());uniform_int_distribution<> dist(0, n-1);vector<int> targets(1000);for (int i = 0; i < 1000; i++) {targets[i] = dist(gen);}// 測試二分查找時間auto start = chrono::high_resolution_clock::now();for (int t : targets) {binarySearch(nums, t);}auto end = chrono::high_resolution_clock::now();chrono::duration<double> binaryTime = end - start;cout << "二分查找總時間：" << binaryTime.count() << "秒" << endl;// 測試三分查找時間start = chrono::high_resolution_clock::now();for (int t : targets) {ternarySearch(nums, t);}end = chrono::high_resolution_clock::now();chrono::duration<double> ternaryTime = end - start;cout << "三分查找總時間：" << ternaryTime.count() << "秒" << endl;return 0;
}

我跑了幾次，二分查找總時間大概在0.0002秒左右，三分查找大概在0.0004秒左右——反而更慢。所以除非是極特殊的場景，否則二分查找是性價比最高的選擇，大家可以親自去試一試。

細節：這些坑別踩

常見問題	正確做法	錯誤案例（為什么錯）
右邊界初始化	right = nums.size() - 1	right = nums.size()（可能導致下標越界）
mid計算	left + (right - left)/2	(left+right)/2（left/right過大時溢出）
循環條件	left <= right	left < right（會漏掉left==right時的元素）

三個點聯動起來記：“閉區間初始化（右邊界取尾下標）+ 安全算 mid + 循環到相等”，二分查找的邊界問題基本就繞不開了

快速測試：你能找出這些錯誤嗎？

int search(vector<int>& nums, int target) {int left = 0, right = nums.size();  while (left < right) {  int mid = (left + right) / 2;  if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}return -1;
}

答案：

1. right應初始化為nums.size()-1
2. 循環條件應是left <= right
3. mid計算應是left + (right - left)/2 （也不算錯誤就是這種寫法更優）

總結+預告

今天我們從“二段性”這個核心點出發，拆解了二分查找的基礎邏輯，通過LeetCode 704題實現了樸素二分查找的代碼，也踩了右邊界初始化、mid計算溢出這些常見的“坑”。其實二分查找的本質就是“用條件劃分范圍，逐步縮小查找空間”，只要抓住這個核心，再復雜的變形也能捋清楚。

不過今天的題目里，數組元素是“不重復”的，所以找到target后直接返回即可。但如果數組里有重復元素，比如[1,2,2,3]，要找2第一次出現的位置或者最后一次出現的位置，樸素二分就不夠用了——這就需要用到我們之前提到的“左邊界查找”和“右邊界查找”模板。

明天要一起研究的是 LeetCode 34題：在排序數組中查找元素的第一個和最后一個位置，有個小問題可以先想想：如果數組是[1,2,2,2,3]，target=2，你覺得“左邊界”和“右邊界”分別是多少？用今天的樸素二分查找，能直接找到嗎？為什么？明天我們就用這個例子拆解“左邊界查找”的邏輯～

“喏，Doro給你一朵小花🌸獎勵看到這里的你，這篇二分查找的拆解有沒有把你心里的‘小疑惑’全捋順呀？要是你覺得這篇博客把單調性、二段性這些‘小細節’講得明明白白，就給個點贊鼓勵一下嘛~ 要是怕以后找不到這么貼心的講解，可得趕緊收藏起來！不然下次遇到二分問題，Doro怕你會像Doro一樣因為找不到 Orange 時那樣‘委屈巴巴’哦~ Doro 知道這個博主后面還會扒更多算法‘小秘密’，關注他，帶你從‘看著會’到‘寫得對’，再也不被二分的細節‘背刺’啦~，最后的最后Doro把這道題的模板寫在這里了，一定要學會再用哦！👇”

樸素二分模板

while(left <= right)
{int mid = left + (right - left)/2;if(.....)//條件left = mid + 1;else if(.....)//條件right = mid -1;elsereturn .....;//找到并返回結果
}