STL關聯式容器解析：map與set詳解

目錄

1. 關聯式容器

2. 鍵值對

3. 樹形結構的關聯式容器

3.1 set

3.1.2 set的使用

3.2 map

3.2.1 map的介紹

3.2.2 map的使用

3.3 multiset

3.3.1 multiset的介紹

3.3.2 multiset的使用

3.4 multimap

3.4.1 multimap的介紹

3.4.2 multimap的使用

4.紅黑樹模擬實現STL中的map與set

4.1紅黑樹的節點定義

4.2 紅黑樹的迭代器

4.3改造紅黑樹

4.4 map的模擬實現

4.5?set的模擬實現

1. 關聯式容器

在初階階段，我們已經接觸過STL中的部分容器，比如：vector、list、deque、 forward_list(C++11)等，這些容器統稱為序列式容器，因為其底層為線性序列的數據結構，里面 存儲的是元素本身。那什么是關聯式容器？它與序列式容器有什么區別？

? 關聯式容器也是用來存儲數據的，與序列式容器不同的是，其里面存儲的是結構的 鍵值對，在數據檢索時比序列式容器效率更高。

2. 鍵值對

? 用來表示具有一一對應關系的一種結構，該結構中一般只包含兩個成員變量key和value，key代 表鍵值，value表示與key對應的信息。比如：現在要建立一個英漢互譯的字典，那該字典中必然 有英文單詞與其對應的中文含義，而且，英文單詞與其中文含義是一一對應的關系，即通過該應 該單詞，在詞典中就可以找到與其對應的中文含義。

3. 樹形結構的關聯式容器

? 根據應用場景的不桶，STL總共實現了兩種不同結構的關聯式容器：樹型結構與哈希結構。樹型結 構的關聯式容器主要有四種：map、set、multimap、multiset。這四種容器的共同點是：使 用平衡搜索樹(即紅黑樹)作為其底層結果，容器中的元素是一個有序的序列。下面一依次介紹每一 個容器。

3.1 set

3.1.1 set的介紹

1. set是按照一定次序存儲元素的容器

2. 在set中，元素的value也標識它(value就是key，類型為T)，并且每個value必須是唯一的。 set中的元素不能在容器中修改(元素總是const)，但是可以從容器中插入或刪除它們。

3. 在內部，set中的元素總是按照其內部比較對象(類型比較)所指示的特定嚴格弱排序準則進行 排序。

4. set容器通過key訪問單個元素的速度通常比unordered_set容器慢，但set允許根據順序（begin到end）對 子集進行直接迭代。

5. set在底層是用二叉搜索樹(紅黑樹)實現的。

注意：

1. 與map/multimap不同，map/multimap中存儲的是真正的鍵值對，set中只放 value，但在底層實際存放的是由構成的鍵值對。

2. set中插入元素時，只需要插入value即可，不需要構造鍵值對。

3. set中的元素不可以重復(因此可以使用set進行去重)。

4. 使用set的迭代器遍歷set中的元素，可以得到有序序列

5. set中的元素默認按照小于來比較

6. set中查找某個元素，時間復雜度為：$log_2 n$

7. set中的元素不允許修改(為什么? 因為底層的紅黑樹是一個升序結構，如果擅自修改節點的值，可能會破壞樹結構)

8. set中的底層使用二叉搜索樹(紅黑樹)來實現。

3.1.2 set的使用

1. set的模板參數列表

T: set中存放元素的類型，實際在底層存儲的鍵值對。

Compare：set中元素默認按照小于來比較

Alloc：set中元素空間的管理方式，使用STL提供的空間配置器管理

2. set的構造

3. set的迭代器

4. set的容量

5. set修改操作

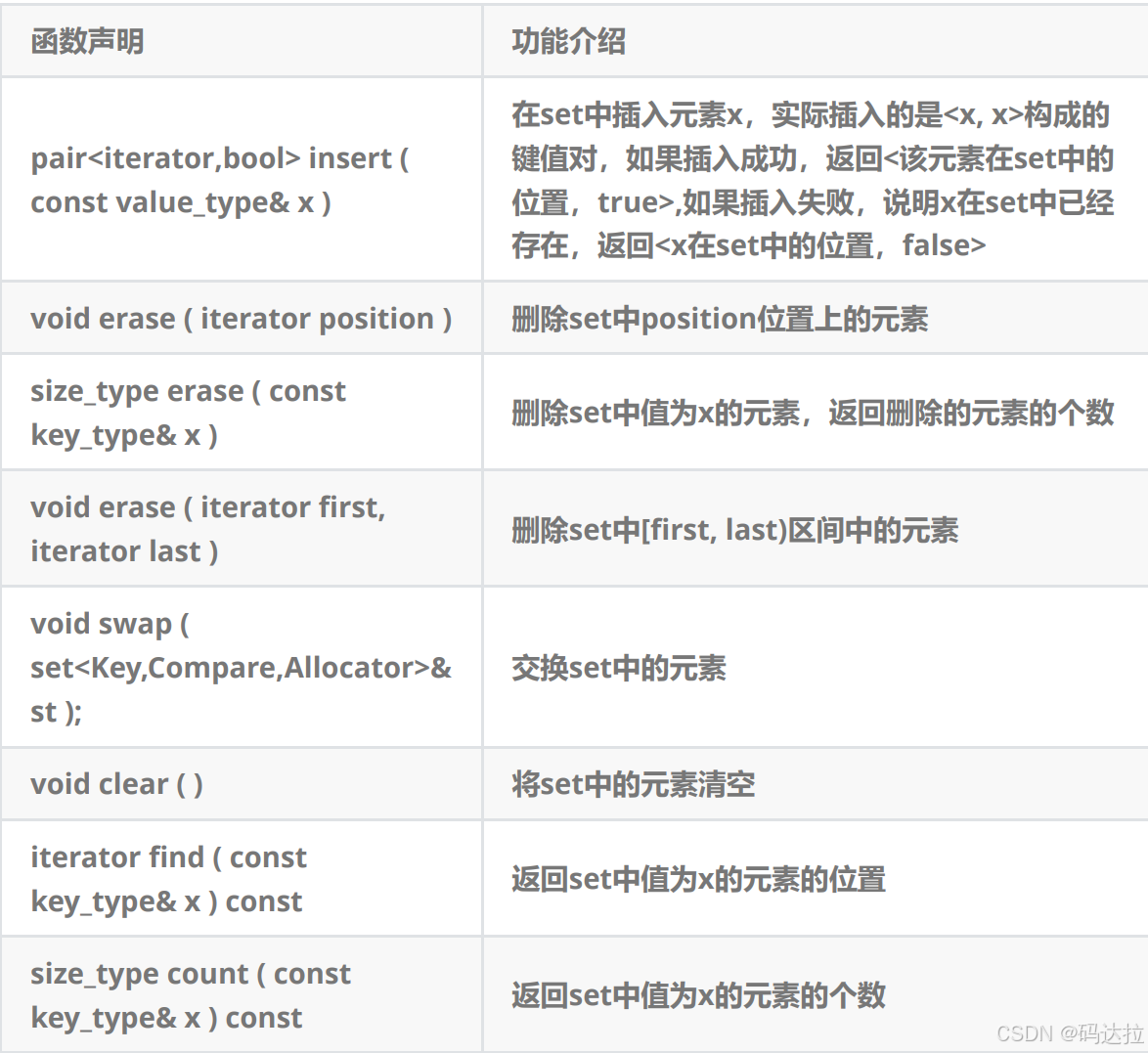
6. set的使用舉例

#include <set>
void TestSet()
{// 用數組array中的元素構造setint array[] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 0, 1, 3, 5, 7, 9, 2, 4, 
6, 8, 0 };set<int> s(array, array+sizeof(array)/sizeof(array[0]));cout << s.size() << endl;// 正向打印set中的元素，從打印結果中可以看出：set可去重for (auto& e : s)cout << e << " ";cout << endl;// 使用迭代器逆向打印set中的元素for (auto it = s.rbegin(); it != s.rend(); ++it)cout << *it << " ";cout << endl;// set中值為3的元素出現了幾次cout << s.count(3) << endl;
}

3.2 map

3.2.1 map的介紹

1. map是關聯容器，它按照特定的次序(按照key來比較)存儲由鍵值key和值value組合而成的元 素。

2. 在map中，鍵值key通常用于排序和唯一地標識元素，而值value中存儲與此鍵值key關聯 的內容。鍵值key和值value的類型可能不同，并且在map的內部，key與value通過成員類 型value_type綁定在一起，為其取別名稱為pair

3. 在內部，map中的元素總是按照鍵值key進行比較排序的。

4. map中通過鍵值訪問單個元素的速度通常比unordered_map容器慢，但map允許根據順序 對元素進行直接迭代(即對map中的元素進行迭代時，可以得到一個有序的序列)。

5. map支持下標訪問符，即在[]中放入key，就可以找到與key對應的value。

6. map通常被實現為二叉搜索樹(更準確的說：平衡二叉搜索樹(紅黑樹))。

3.2.2 map的使用

1. map的模板參數說明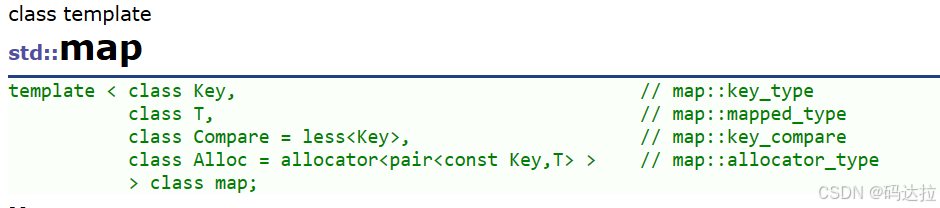

key: 鍵值對中key的類型

T： 鍵值對中value的類型

Compare: 比較器的類型，map中的元素是按照key來比較的，缺省情況下按照小于來比 較，一般情況下(內置類型元素)該參數不需要傳遞，如果無法比較時(自定義類型)，需要用戶 自己顯式傳遞比較規則(一般情況下按照函數指針或者仿函數來傳遞)

Alloc：通過空間配置器來申請底層空間，不需要用戶傳遞，除非用戶不想使用標準庫提供的 空間配置器 注意：

在使用map時，需要包含頭文件。

2. map的構造

3. map的迭代器

4. map的容量與元素訪問

問題：當key不在map中時，通過operator獲取對應value時會發生什么問題？將鍵值對插入；

? 注意：在元素訪問時，有一個與operator[]類似的操作at()(該函數不常用)函數，都是通過 key找到與key對應的value然后返回其引用，不同的是：當key不存在時，operator[]用默認 value與key構造鍵值對然后插入，返回該默認value，at()函數直接拋異常。

5. map中元素的修改

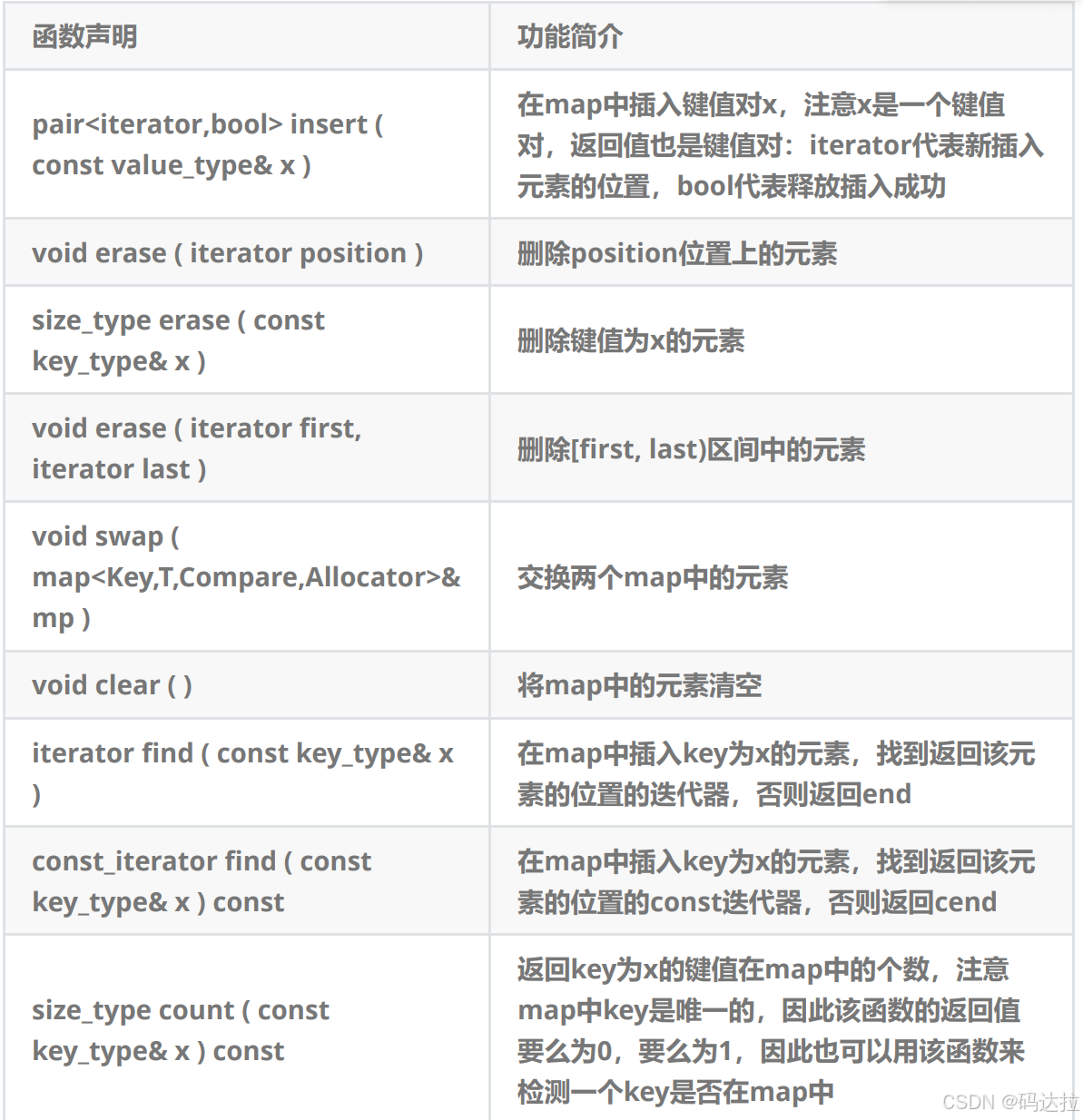
【總結】

1. map中的的元素是鍵值對

2. map中的key是唯一的，并且不能修改

3. 默認按照小于的方式對key進行比較

4. map中的元素如果用迭代器去遍歷，可以得到一個有序的序列

5. map的底層為平衡搜索樹(紅黑樹)，查找效率比較高$O(log_2 N)$

6. 支持[]操作符，operator[]中實際進行插入查找。

3.3 multiset

3.3.1 multiset的介紹

1. multiset是按照特定順序存儲元素的容器，其中元素是可以重復的。

2. 在multiset中，元素的value也會識別它(因為multiset中本身存儲的就是組成 的鍵值對，因此value本身就是key，key就是value，類型為T). multiset元素的值不能在容器 中進行修改(因為元素總是const的)，但可以從容器中插入或刪除。

3. 在內部，multiset中的元素總是按照其內部比較規則(類型比較)所指示的特定嚴格弱排序準則 進行排序。

4. multiset容器通過key訪問單個元素的速度通常比unordered_multiset容器慢，但當使用迭 代器遍歷時會得到一個有序序列。

5. multiset底層結構為二叉搜索樹(紅黑樹)。

注意：

1. multiset中在底層中存儲的是的鍵值對

2. multiset的插入接口中只需要插入即可

3. 與set的區別是，multiset中的元素可以重復，set中value是唯一的

4. 使用迭代器對multiset中的元素進行遍歷，可以得到有序的序列

5. multiset中的元素不能修改

6. 在multiset中找某個元素，時間復雜度為$O(log_2 N)$

7. multiset的作用：可以對元素進行排序

3.3.2 multiset的使用

此處只簡單演示set與multiset的不同，其他接口接口與set相同，同學們可參考set。

#include <set>
void TestSet()
{int array[] = { 2, 2, 3, 9, 6, 0, 5, 8, 4, 7 };// 注意：multiset在底層實際存儲的是<int, int>的鍵值對multiset<int> s(array, array + sizeof(array)/sizeof(array[0]));for (auto& e : s)cout << e << " ";cout << endl;return 0;
}

3.4 multimap

3.4.1 multimap的介紹

1. Multimaps是關聯式容器，它按照特定的順序，存儲由key和value映射成的鍵值對，其中多個鍵值對之間的key是可以重復的。

2. 在multimap中，通常按照key排序和惟一地標識元素，而映射的value存儲與key關聯的內 容。key和value的類型可能不同，通過multimap內部的成員類型value_type組合在一起， value_type是組合key和value的鍵值對: typedef pair value_type;

3. 在內部，multimap中的元素總是通過其內部比較對象，按照指定的特定嚴格弱排序標準對 key進行排序的。

4. multimap通過key訪問單個元素的速度通常比unordered_multimap容器慢，但是使用迭代 器直接遍歷multimap中的元素可以得到關于key有序的序列。

5. multimap在底層用二叉搜索樹(紅黑樹)來實現。

? 注意：multimap和map的唯一不同就是：map中的key是唯一的，而multimap中key是可以 重復的。

3.4.2 multimap的使用

multimap中的接口可以參考map，功能都是類似的。

注意：

1. multimap中的key是可以重復的。

2. multimap中的元素默認將key按照小于來比較

3. multimap中沒有重載operator[]操作(為什么?)。

??multimap允許存儲多個相同鍵的元素，這使得operator[]的行為變得不明確。當使用operator[]訪問一個存在多個相同鍵的multimap時，應該返回哪個值？是第一個匹配的值、最后一個匹配的值，還是所有匹配的值？這種歧義使得operator[]在multimap中的實現變得復雜且不符合直觀。

4. 使用時與map包含的頭文件相同：

4.紅黑樹模擬實現STL中的map與set

雖然之前已經寫過紅黑樹的模擬實現，但在這里會有所不同。

4.1紅黑樹的節點定義

enum Color
{Red,Black
};
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;RBTreeNode(const T& key):_data(key), _left(nullptr), _right(nullptr), _parent(nullptr), _col(Red){}
};

? 注意這里只用了T這一個模版參數，因為一個T既可以存儲單一類型也可以存儲pair類型，因此K模型和KV模型都可以支持！

4.2 紅黑樹的迭代器

? ?迭代器的好處是可以方便遍歷，是數據結構的底層實現與用戶透明。如果想要給紅黑樹增加迭代 器，需要考慮以前問題：

? begin()與end() STL明確規定，begin()與end()代表的是一段前閉后開的區間，而對紅黑樹進行中序遍歷后， 可以得到一個有序的序列，因此：begin()可以放在紅黑樹中最小節點(即最左側節點)的位 置，end()放在最大節點(最右側節點)的下一個位置，關鍵是最大節點的下一個位置在哪塊？ 這里我們將end處給上nullptr，當要執行end--的時候，我們要確保能回到最大節點處。

下面給出紅黑樹的迭代器封裝，思路體現在注釋里：

//紅黑樹的迭代器封裝，其實就是對某個節點指針的封裝；
//begin位于最小的節點，end位于最大節點的下一個位置
//紅黑樹的end迭代器，我們設該節點為空指針，且由于我們要滿足end--能回到最大元素的位置，就要用到根節點_root
template<class T, class Ref, class Ptr>
struct Iterator
{using Node = RBTreeNode<T>;using Self = Iterator<T, Ref, Ptr>;Node* _node;Node* _root;Iterator(Node* node, Node* root):_node(node),_root(root){}//引用迭代器，直接返回數據data的引用Ref operator*(){return _node->_data;}//it->,返回的是數據data的指針，編譯器會優化一次->操作//對于set，->可以直接返回數據，或返回類對象的成員變量//對于map，存儲的是pair類型，可以直接用it->first,it->secondPtr operator->(){return &_node->_data;}bool operator==(const Self& it){return _node->_data == it._node->_data;}bool operator!=(const Self& it){return _node != it._node;}//按照順序返回下一個數據的節點Self& operator++(){//如果當前節點的右側還有節點，就找出右側的最小節點if (_node->_right){Node* rightmin = _node->_right;while (rightmin->_left){rightmin = rightmin->_left;}_node = rightmin;}//否則，找出第一個左指針指向當前節點的節點，如果遇到父節點為空了，說明已經到根節點了，// 也就是最初的cur為最大節點，_node最后就應該指向空指針(end),符合迭代器思想else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}//按照順序返回上一個數據的節點Self& operator--(){//這種情況是從end--，應該回到最大節點處if (_node == nullptr){Node* rightmax = _root;while (rightmax->_right){rightmax = rightmax->_right;}_node = rightmax;}//如果當前節點的左側還有節點，就找出左側的最大節點else if (_node->_left){Node* leftmax = _node->_left;while (leftmax->_right){leftmax = leftmax->_right;}_node = leftmax;}//否則，找出第一個右指針指向當前節點的節點，如果遇到父節點為空了，說明已經到根節點了，// 也就是最初的cur為最小節點，_node最后就應該指向空指針(end),符合迭代器思想else{Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_left == cur){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}
};

4.3改造紅黑樹

??因為關聯式容器中存儲的是的鍵值對：

? T是存儲的數據類型，可能是單一類型，也可能是pair類型，因此我們無法確定T的鍵值類型以及如何取鍵值，
? ?KeyofT是取鍵值的方式，Compare是比較邏輯

//因為T是存儲的數據類型，可能是單一類型，也可能是pair類型，因此我們無法確定T的鍵值類型以及如何取鍵值，
// KeyofT是取鍵值的方式，Compare是比較邏輯
template<class K, class T, class KeyofT,class Compare = myless<K>>
class RBTree
{
public:using Node = RBTreeNode<T>;using iterator = Iterator<T, T&, T*>;using const_iterator = Iterator<T, const T&, const T*>;iterator begin(){Node* leftmin = _root;while (leftmin && leftmin->_left){leftmin = leftmin->_left;}return iterator(leftmin, _root);}iterator end(){return iterator(nullptr, _root);}const_iterator begin() const{Node* leftmin = _root;while (leftmin && leftmin->_left){leftmin = leftmin->_left;}return const_iterator(leftmin, _root);}const_iterator end() const{return const_iterator(nullptr, _root);}RBTree() = default;RBTree(const RBTree<K, T, KeyofT, Compare>& t){_root = Copy(t._root);}Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* newroot = new Node(root->_data);newroot->_parent = root->_parent;newroot->_color = root->_color;newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}RBTree<K, T, KeyofT,Compare >& operator=(RBTree t){swap(_root, t._root);return *this;}~RBTree(){Destroy(_root);_root = nullptr;}void Destroy(Node* root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}void inorder(){Inorder(_root);}void Inorder(Node* root){if (root == nullptr){return;}Inorder(root->_left);cout << root->_data.first << ' ' << root->_data.second << endl;Inorder(root->_right);}iterator find(const K& key){Compare comp;KeyofT key;Node* cur = _root;while (cur){if (comp(key(cur->_data), key)){cur = cur->_right;}else if (!comp(key(cur->_data), key)){cur = cur->_left;}else{return iterator(cur, _root);}}return end();}pair<iterator,bool> insert( T& data){Compare comp;KeyofT key;if (_root == nullptr){_root = new Node(data);_root->_color = Black;return make_pair(iterator(_root,_root),true);}Node* cur = _root;Node* parent = nullptr;while (cur){if (comp(key(cur->_data), key(data))){parent = cur;cur = cur->_right;}else if (!comp(key(cur->_data), key(data))){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur, _root), false);}}cur = new Node(data);if (comp(key(parent->_data), key(data))){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//進行顏色調整while (parent && parent->_color == Red){Node* grand = parent->_parent;Node* uncle = nullptr;if (parent == grand->_left){uncle = grand->_right;if (uncle && uncle->_color == Red){parent->_color = uncle->_color = Black;grand->_color = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grand);grand->_color = Red;parent->_color = Black;break;}else{RotateL(parent);RotateR(grand);cur->_color = Black;grand->_color = Red;break;}}}else{uncle = grand->_left;if (uncle && uncle->_color == Red){parent->_color = uncle->_color = Black;grand->_color = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grand);grand->_color = Red;parent->_color = Black;break;}else{RotateR(parent);RotateL(grand);cur->_color = Black;grand->_color = Red;break;}}}}_root->_color = Black;return make_pair(iterator(cur, _root), true);}
private:void RotateR(Node* parent){Node* cur = parent->_left;Node* cr = cur->_right;parent->_left = cr;if (cr){cr->_parent = parent;}Node* pparent = parent->_parent;cur->_right = parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}}void RotateL(Node* parent){Node* cur = parent->_right;Node* cr = cur->_left;parent->_right = cr;if (cr){cr->_parent = parent;}Node* pparent = parent->_parent;cur->_left = parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}}
private:Node* _root = nullptr;
};

4.4 map的模擬實現

map的底層結構就是紅黑樹，因此在map中直接封裝一棵紅黑樹，然后將其接口包裝下即可

#include "RBTree.hpp"template<class K,class V>
class Map
{
public:class KeyofT{public:const K& operator()(const pair<K,V>& x){return x.first;}};using iterator = typename RBTree<K, pair<const K,V>, KeyofT>::iterator;using const_iterator = typename RBTree<K, pair<const K, V>, KeyofT>::const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin()const{return _t.begin();}const_iterator end()const{return _t.end();}iterator find(const K& x){return _t.find(x);}pair<iterator, bool> insert(  pair<const K, V> x){return _t.insert(x);}V& operator[](const K& key){pair<iterator, bool> ret = insert({ key,K() });auto it = ret.first;return it->second;}
private:RBTree<K, pair<const K, V>, KeyofT> _t;
};

4.5?set的模擬實現

? set的底層為紅黑樹，因此只需在set內部封裝一棵紅黑樹，即可將該容器實現出來(具體實現可參 考map)。

#include "RBTree.hpp"template<class K>
class Set
{
public:class KeyofT{public:const K& operator()(const K& x){return x;}};using iterator = typename RBTree<K,const K, KeyofT>::iterator;using const_iterator = typename RBTree<K, const K, KeyofT>::const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin()const{return _t.begin();}const_iterator end()const{return _t.end();}iterator find(const K& x){return _t.find(x);}pair<iterator, bool> insert(const K& x){return _t.insert(x);}
private:RBTree<K, const K, KeyofT> _t;
};

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/919775.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/919775.shtml
英文地址，請注明出處：http://en.pswp.cn/news/919775.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

貪吃蛇--C++實戰項目（零基礎）

貪吃蛇--C++實戰項目（零基礎）

視頻地址&#xff1a;C語言必學項目&#xff1a;貪吃蛇&#xff01; 貪吃蛇游戲框架 ├── 基礎框架 │ ├── 頭文件引入 │ ├── 常量和宏定義 │ └── 窗口初始化 │ ├── 數據結構系統 │ ├── Pos結構體(位置和顏色) │ ├── Snake結構體(蛇的屬性) │ ├──…
閱讀更多...
unity資源領取反作弊工具加密器

unity資源領取反作弊工具加密器

https://assetstore.unity.com/packages/tools/utilities/anti-cheat-pro-2025-3006260元購碼GUARDINGPEARSOFTWARE
閱讀更多...
FPGA設計中的信號完整性量化與優化：探索高速數字系統的關鍵路徑

FPGA設計中的信號完整性量化與優化：探索高速數字系統的關鍵路徑

在高速FPGA設計中&#xff0c;信號完整性&#xff08;Signal Integrity, SI&#xff09;已成為確保系統穩定、可靠運行的核心要素之一。隨著數據傳輸速率的不斷提升和電路規模的日益復雜&#xff0c;信號在傳輸過程中受到的干擾和畸變問題日益凸顯。因此&#xff0c;如何有效量…
閱讀更多...
`strncasecmp` 字符串比較函數

`strncasecmp` 字符串比較函數

1) 函數的概念與用途 strncasecmp 是 C 語言中一個非常實用的字符串處理函數&#xff0c;它執行不區分大小寫的字符串比較&#xff0c;但只比較前 n 個字符。這個函數的名字來源于"string n case-compare"&#xff08;字符串前n個字符不區分大小寫比較&#xff09;。…
閱讀更多...
軟件安裝教程（一）：Visual Studio Code安裝與配置（Windows）

軟件安裝教程（一）：Visual Studio Code安裝與配置（Windows）

文章目錄前言一、Visual Studio Code下載二、安裝步驟&#xff08;Windows&#xff09;1. GUI安裝2. 命令行安裝三、首次啟動后建議的快速配置&#xff08;幾分鐘完成&#xff09;四、常見問題 & 小貼士總結前言 Visual Studio Code&#xff08;VS Code&#xff09;是一款…
閱讀更多...
JavaSSM框架從入門到精通！第三天(MyBatis(二))！

JavaSSM框架從入門到精通！第三天(MyBatis(二))！

四、Mapper 的動態代理1. 引入 在上面的 CURD 例子中&#xff0c;我們發現&#xff1a;Dao 層的實現類的每一個方法僅僅是通過 SqlSession 對象的相關 API 定位到映射文件 mapper 中的 SQL 語句&#xff0c;真正對數據庫操作的工作實際上是有 Mybatis 框架通過 mapper 中的 SQL…
閱讀更多...
大模型應用發展與Agent前沿技術趨勢（下）

大模型應用發展與Agent前沿技術趨勢（下）

Agent技術的行業應用與實踐案例 金融領域的Agent應用 金融行業是大模型Agent技術應用最為廣泛的領域之一&#xff0c;涵蓋了風險評估、投資決策、客戶服務等多個方面。在金融風控領域&#xff0c;Agent系統通過結合大模型的語義理解能力和強化學習的決策優化能力&#xff0c;能…
閱讀更多...
94. 城市間貨物運輸 I, Bellman_ford 算法, Bellman_ford 隊列優化算法

94. 城市間貨物運輸 I, Bellman_ford 算法, Bellman_ford 隊列優化算法

94. 城市間貨物運輸 IBellman_ford 算法Bellman_ford 算法 與 dijkstra算法 相比通用性更強。dijkstra算法解決不了負權邊的問題&#xff0c;因為Dijkstra基于貪心策略&#xff0c;一旦一個節點被從隊列中取出&#xff08;標記為已解決&#xff09;&#xff0c;它就假定已經找到…
閱讀更多...
如何使用Prometheus + Grafana + Loki構建一個現代化的云原生監控系統

如何使用Prometheus + Grafana + Loki構建一個現代化的云原生監控系統

如何使用 Prometheus + Grafana + Loki 構建一個現代化的云原生監控系統。這套組合被譽為監控領域的“瑞士軍刀”，功能強大且生態極佳。 一、核心組件概念介紹 在搭建之前，深刻理解每個組件的角色和職責至關重要。 1. Prometheus（指標監控與時序數據庫） 角色：系統的“核…
閱讀更多...
JavaScript Object 操作方法及 API

JavaScript Object 操作方法及 API

一、對象創建方式1.字面量創建&#xff08;最常用&#xff09;const obj { name: "張三", age: 25 };2.構造函數創建const obj new Object(); obj.name "李四";3.Object.create()&#xff08;指定原型&#xff09;const proto { greet: () > "…
閱讀更多...
pta乙級題目day1

pta乙級題目day1

第1天&#xff1a;輸入輸出與運算&#xff08;6題&#xff09;1001 害死人不償命的(3n1)猜想&#xff08;基礎運算&#xff09;★1006 換個格式輸出整數&#xff08;格式化輸出&#xff09;★1016 部分AB&#xff08;數字提取&#xff09;★★1046 劃拳&#xff08;多輸入處理&…
閱讀更多...
在VSCode中配置.NET項目的tasks.json以實現清理、構建、熱重載和發布等操作

在VSCode中配置.NET項目的tasks.json以實現清理、構建、熱重載和發布等操作

在 VS Code 中配置 .NET 開發任務的完整指南 引言 重要提醒&#xff1a;對于 .NET 開發&#xff0c;強烈推薦使用 Visual Studio&#xff0c;它提供了最完整和穩定的開發體驗。如果你像我一樣"蛋疼"想要嘗試 VS Code&#xff0c;請確保安裝了 C# 開發擴展包&#x…
閱讀更多...
EmEditor文本編輯器v25.3.0專業版，專業文本編輯，高亮顯示，無限撤消

EmEditor文本編輯器v25.3.0專業版，專業文本編輯，高亮顯示，無限撤消

[軟件名稱]: EmEditor文本編輯器v25.3.0專業版 [軟件大小]: 37.7 MB [軟件大小]: 夸克網盤 | 百度網盤 軟件介紹 EmEditor 是一款功能強大且非常實用的文本編輯器。它啟動速度快&#xff0c;完全可以替代 Windows 自帶的記事本&#xff0c;輕松應對日常文本編輯任務。它對 …
閱讀更多...
【spring security】權限管理組件執行流程詳解

【spring security】權限管理組件執行流程詳解

&#x1f3af; 權限管理組件執行流程詳解 &#x1f3d7;? 組件架構圖 ┌─────────────────────────────────────────────────────────────┐ │ HTTP請求 …
閱讀更多...
redis怎么保障雙寫一致性

redis怎么保障雙寫一致性

redis做為緩存&#xff0c;mysql的數據如何與redis進行同步呢&#xff1f;&#xff08;雙寫一致性&#xff09;候選人&#xff1a;嗯&#xff01;就說我最近做的這個項目&#xff0c;里面有xxxx&#xff08;根據自己的簡歷上寫&#xff09;的功能&#xff0c;需要讓數據庫與red…
閱讀更多...
異常值檢測：孤立森林模型（IsolationForest）總結

異常值檢測：孤立森林模型（IsolationForest）總結

目錄一、前言二、孤立森林算法2.1 算法簡介2.2 基本原理2.3 算法步驟2.4 異常分數計算方式2.5 python調用方式三、python代碼示例四、小結五、參考學習一、前言 近期在研究構建壽命預測模型&#xff0c;相信很多數據人都懂建模的過程&#xff0c;其實有80%的時間都是在和數據處…
閱讀更多...
Docker容器化部署實戰：Tomcat與Nginx服務配置指南

Docker容器化部署實戰：Tomcat與Nginx服務配置指南

部署Tomcat搜索鏡像 使用以下命令搜索可用的Tomcat鏡像&#xff1a;docker search tomcat拉取鏡像 拉取官方Tomcat鏡像&#xff1a;docker pull tomcat創建專用目錄 為Tomcat配置和數據創建專用目錄&#xff1a;mkdir tomcat運行臨時容器并復制配置文件 啟動臨時容器以復制配置…
閱讀更多...
Go語言實戰案例-使用SQLite實現本地存儲

Go語言實戰案例-使用SQLite實現本地存儲

在開發工具類軟件、桌面應用或者移動端時&#xff0c;我們經常需要一個輕量級數據庫來做 本地存儲。相比 MySQL、Postgres 等服務型數據庫&#xff0c;SQLite 體積小、零配置、單文件存儲&#xff0c;非常適合這種場景。Go 語言通過 GORM SQLite 驅動 就能輕松實現。本文將帶你…
閱讀更多...
云計算學習100天-第23天

云計算學習100天-第23天

主機192.168.88.5 安裝nginx#安裝編譯工具&#xff0c;正則表達式依賴包&#xff0c;SSL加密依賴包 yum -y install gcc make pcre-devel openssl-devel tar -xf /root/lnmp_soft.tar.gz cd lnmp_soft/ tar -xf nginx-1.22.1.tar.gz cd nginx-1.22.1/ #指定安裝路徑&…
閱讀更多...
【生成樹+環】題解：P3907 環的異或_圖論_環_異或_搜索_算法競賽_C++

【生成樹+環】題解：P3907 環的異或_圖論_環_異或_搜索_算法競賽_C++

推銷洛谷博客&#xff1a;https://www.luogu.com.cn/article/znmr9iu9 Link&#xff1a;Luogu - P3907 這里默認題目中指的環都是“簡單環”&#xff08;即沒有“環套環”的情況&#xff09;。 眾所周知&#xff0c;樹是圖的一種特殊情況&#xff0c;且一定無環。如果我們想…
閱讀更多...
最新文章

Copyright @ 2022~2023