目錄

文章目錄

前言

一、記憶化搜索

二、題目概略

三、斐波拉契數

四、Function

五、天下第一

六、滑雪

總結

---

親愛的讀者朋友們，大家好啊！不同的時間，相同的地點，今天又帶來了關于搜索部分的講解。接下來我將接著我前面文章的內容，開始講解以下記憶化搜索的部分了。

let's go!

---

前言

前面我們講解了剪枝的內容，我們接著它，繼續剪枝。

記憶化搜索就是我們剪枝的一大部分，我們接下來就學習我們的記憶化搜索吧！

---

一、記憶化搜索

記憶化搜索也是一種剪枝的策略

通過?個"備忘錄"，記錄第?次搜索到的結果，當下?次搜索到這個狀態時，直接在"備忘錄"??找結果。

我們接下來就看看這部分的題目，在題目中來理解記憶化搜索吧

二、題目概略

509. 斐波那契數 - 力扣（LeetCode）

P1464 Function - 洛谷

P5635 【CSGRound1】天下第一 - 洛谷

P1434 [SHOI2002] 滑雪 - 洛谷

三、斐波拉契數

我們看完題目后，會發現很簡單，一個簡單的遞歸就可以解決了，所以我們很快就可以寫出這道題：

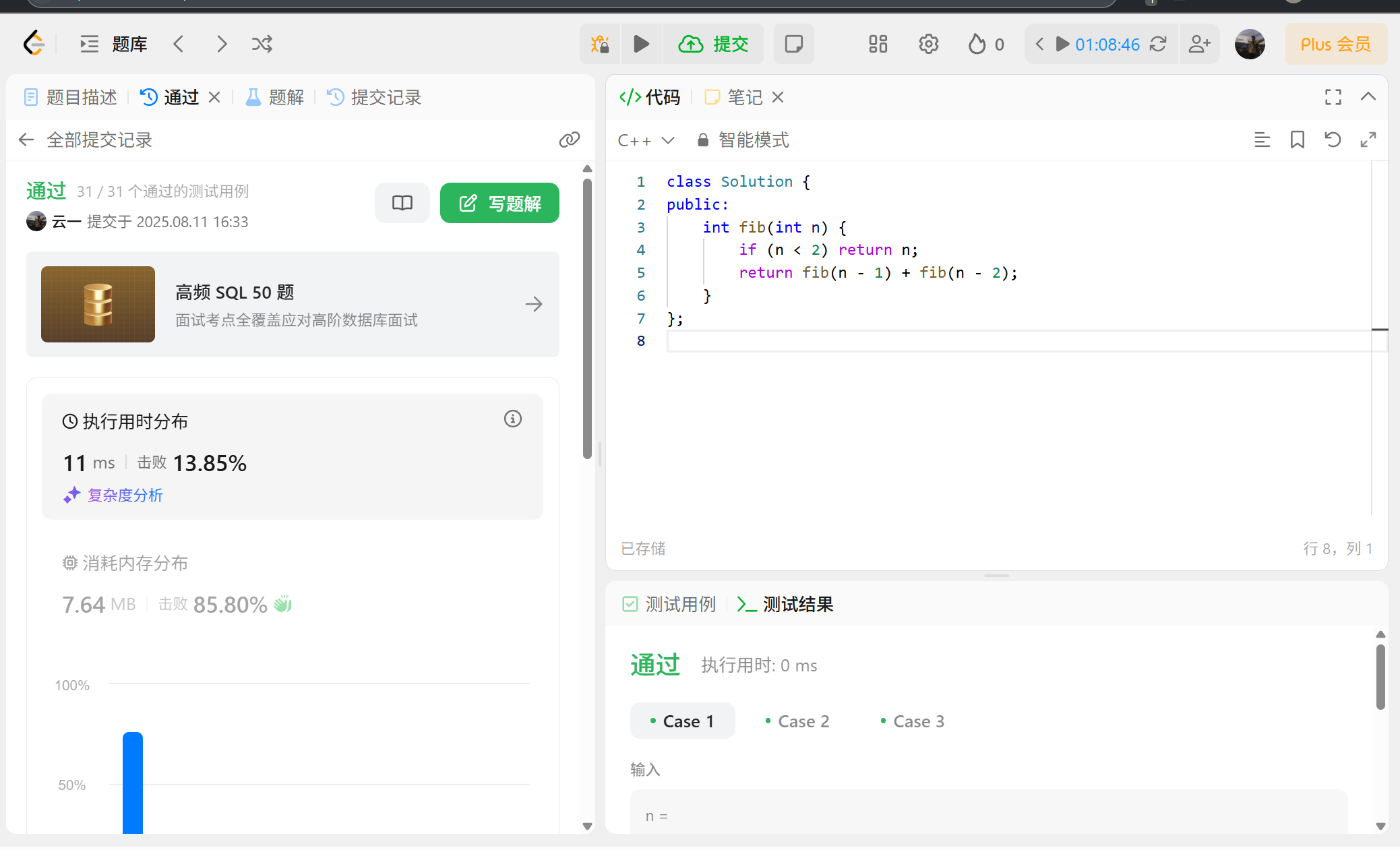
但是？我們執行時間怎么這么多？

如果卡時間我們不就過不了了嗎，所以該怎么辦？

我們畫一下對應的決策樹：

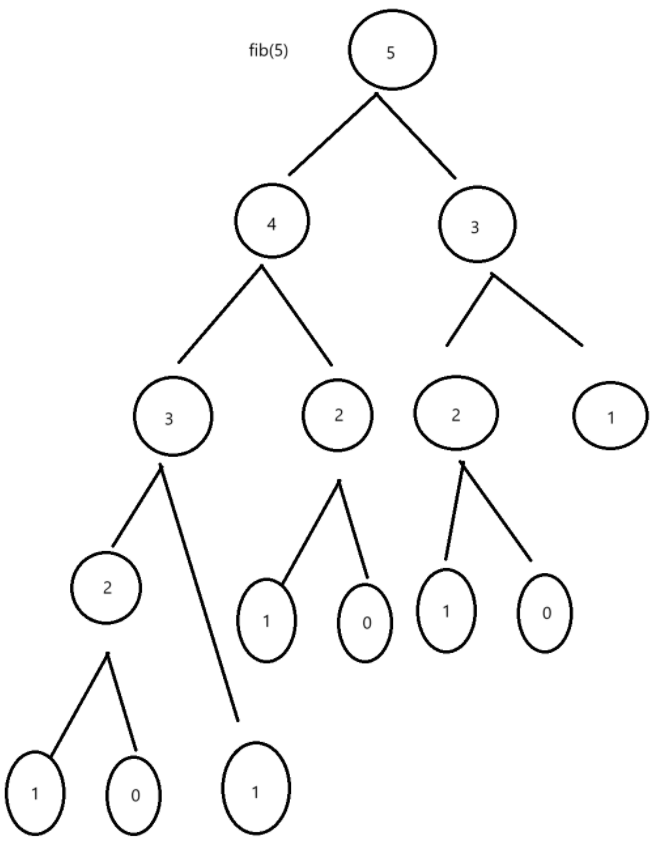
我們發現在遞歸的過程中，會出現很多重復的展開，我們就需要去將這些重復的內容全部去掉才對。這時候我們記憶化搜索就可以來幫助我們了

我們可以將對應的遞歸結果存下來，如果再次需要去遞歸這個數，那么我們判斷一下，直接拿對應的值即可

可以看一下它的數據范圍是小于等于30，所以我們創建一個35大小的數組即可：

int f[35];//備忘錄，存放對應下標i的斐波拉契值

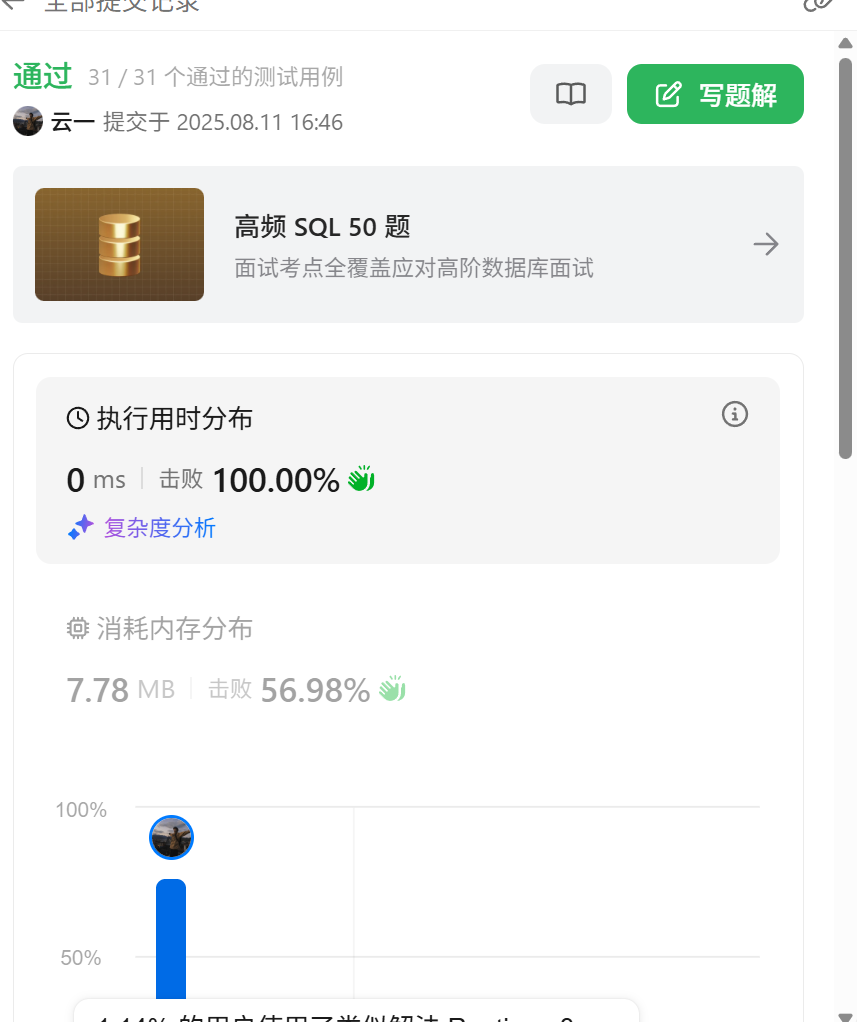
這樣，我們就大幅度的降低了我們的時間消耗。記憶化搜索就幫我們剪掉對應的那些重復枝丫。

四、Function

首先，先理解一下這個題目：

我們無非就是要設計一個遞歸函數，從之前的學習后，寫一個遞歸函數難度肯定不大。

但是題目后面又說，如果出現如w(15, 15, 15)的時候會出現很多的調用，這個時候我們就得需要記憶化搜索來記錄它的結果，剪掉多余的枝丫。

我們來實現一下最簡單的版本：

#include <iostream>
using namespace std;
typedef long long LL;
LL a, b, c;
LL dfs(LL a, LL b, LL c)
{if (a <= 0 || b <= 0 || c <= 0) return 1;if (a > 20 || b > 20 || c > 20) return dfs(20, 20, 20);if (a < b && b < c){return dfs(a, b, c - 1) + dfs(a, b - 1, c - 1) - dfs(a, b - 1, c);}else {return dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a - 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);}
}
int main()
{while(cin >> a >> b >> c){if (a == -1 && b == - 1 && c == -1) break;printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, dfs(a, b, c));}return 0;
}

這是沒有記憶化搜索的版本，我們看看能不能通過呢？

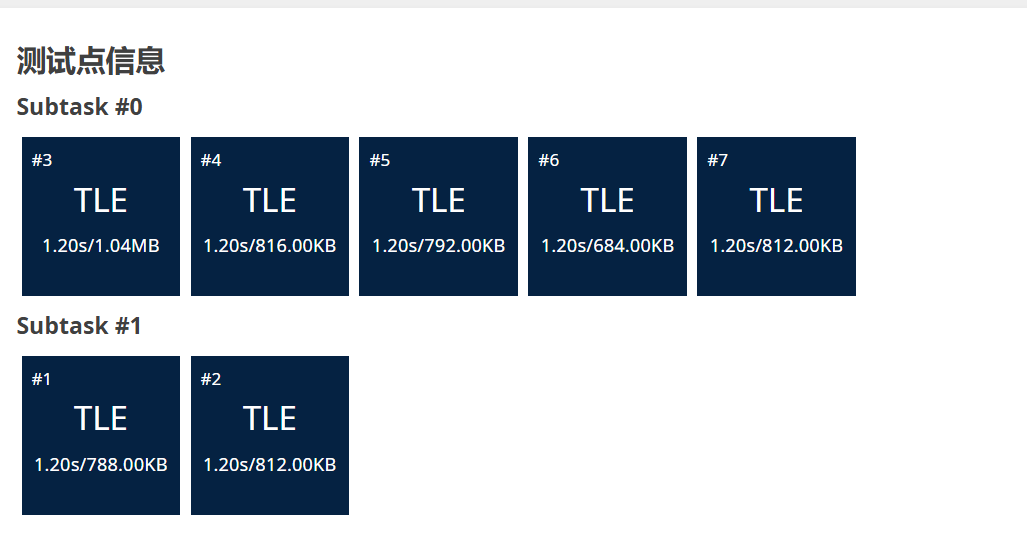
會發現全部都超時了，所以我們的記憶化搜索是必須要增加上去的：

由于這里有三個數，我們要通過三個數來映射對應的值，所以我們要使用一個三維數組去映射：

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 25;
LL f[N][N][N]; 
LL a, b, c;
LL dfs(LL a, LL b, LL c)
{if (a <= 0 || b <= 0 || c <= 0) return 1;if (a > 20 || b > 20 || c > 20) return dfs(20, 20, 20);if (f[a][b][c]) return f[a][b][c];//查找備忘錄 if (a < b && b < c){return f[a][b][c] = dfs(a, b, c - 1) + dfs(a, b - 1, c - 1) - dfs(a, b - 1, c);}else {return f[a][b][c] = dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a - 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);}
}
int main()
{while(cin >> a >> b >> c){if (a == -1 && b == - 1 && c == -1) break;printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, dfs(a, b, c));}return 0;
}

我們這樣就通過了！

可能會有讀者問，為什么多組測試數據不清理數組呢？

那是因為我們后面也會用到這個備忘錄，并不需要清理

五、天下第一

講這道題的時候我需要先講一下取模運算的一些內容

對于取模的加法和乘法的性質：

(a + b + c) % p = (a % p + b % p + c % p) % p

(a * b * c) % p = (a % p * b % p * c % p) % p

在加法和乘法中，括號里面那一坨可以隨便加%p，并不會影響結果

那么現在再來理解一下這道題吧：

我們會有一個x和一個y進行不停的執行取模，誰先到0，誰就贏

都不能到0，就平局

題目很簡單，只需要通過遞歸去解決這個相同子問題即可：

還有就是每次x和y都會更新x = (x + y) % p, y = ((x + y) % p + y) % p = (x + y + y) % p

在不停的模中，就會出現重復的情況，我們就需要記錄下對應的結果

#include <iostream>
using namespace std;
const int N = 1e4 + 10;
char f[N][N];
int T, p;
char dfs(int x, int y)
{if (f[x][y]) return f[x][y];f[x][y] = '3';if (x == 0) return f[x][y] = '1';else if (y == 0) return f[x][y] = '2';return f[x][y] = dfs((x + y) % p, (x + y + y) % p);
}
int main()
{cin >> T >> p;while(T--){int x, y;cin >> x >> y;char ret = dfs(x, y);if (ret == '1') cout << 1 << endl;else if (ret == '2') cout << 2 << endl;else cout << "error" << endl;}return 0;
}

我們由于有x和y，就采用一個二維數組來映射即可

因為有三種結果，我們就不能直接使用bool數組來標記了，我們可以使用int或者char去記錄

但是int沒必要，有些浪費空間了，我們直接使用char數組去記錄即可。

我們一旦進入函數就要給它先打上平局的'3'才行，如果x或者y成了0，就修改為對應的1或者2

如果沒有最后返回的便是平局

六、滑雪

這道題跟前面幾道題的難度就不一樣了

我們最簡單的方法就是枚舉i,j

從（i, j）位置向四個方向去走，將最長的路徑找出來

dfs(i, j)返回這個點能滑的最遠距離

那么怎么讓這個往四個方向去走呢，看過前面章節內容的讀者就知道這時候我們就需要方向數組：dx[]和dy[]去更新我們的x和y了

我們先將最簡單代碼來寫一下：

#include <iostream>
using namespace std;
const int N = 110;
int a[N][N];
int r, c;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int dfs(int i, int j)
{int len = 1;for (int k = 0; k < 4; k++){int x = i + dx[k];int y = j + dy[k];if (x >= 1 && x <= r && y >= 1 && y <= c&& a[x][y] < a[i][j]){len = max(len, dfs(x, y) + 1);}}return len;
}int main()
{cin >> r >> c;for (int i = 1; i <= r; i++){for (int j = 1; j <= c; j++){cin >> a[i][j];}}int ret = 1;for (int i = 1; i <= r; i++){for (int j = 1; j <= c; j++){ret = max(ret, dfs(i, j));}}cout << ret << endl;return 0;
}

我們會發現還是有個例子超時了，我們不加記憶化搜索還是過不了。

由于每次去遍歷的時候都會遍歷到很多之前走過的節點，我們去遍歷的話就會浪費很多時間

我們就得想辦法將每個訪問過的點記憶下來，這樣再訪問這個點就可以直接拿到對應的值了。

#include <iostream>
using namespace std;
const int N = 110;
int a[N][N];
int r, c;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int f[N][N];
int dfs(int i, int j)
{if(f[i][j]) return f[i][j];int len = 1;for (int k = 0; k < 4; k++){int x = i + dx[k];int y = j + dy[k];if (x >= 1 && x <= r && y >= 1 && y <= c&& a[x][y] < a[i][j]){len = max(len, dfs(x, y) + 1);}}return f[i][j] = len;
}int main()
{cin >> r >> c;for (int i = 1; i <= r; i++){for (int j = 1; j <= c; j++){cin >> a[i][j];}}int ret = 1;for (int i = 1; i <= r; i++){for (int j = 1; j <= c; j++){ret = max(ret, dfs(i, j));}}cout << ret << endl;return 0;
}

我們發現這道題難度不大，只要通過深度搜索我們就可以很簡單的將對應的代碼寫出來。

通過添加映射的備忘錄將值記錄即可。

但是要注意的是，一定是要出現大量的相同的情況，我們才去使用備忘錄，記憶化搜索。

如上這樣會訪問到很多相同節點一般。

我們就要去使用記憶化搜索剪枝

---

總結

親愛的讀者朋友們，這篇文章希望大家能夠看完前面的文章再來讀，這樣的話會更加得心應手。

希望大家多多點贊 +?收藏 + 關注！