📝前言說明:
- 本專欄主要記錄本人的基礎算法學習以及LeetCode刷題記錄,按專題劃分
- 每題主要記錄:(1)本人解法 + 本人屎山代碼;(2)優質解法 + 優質代碼;(3)精益求精,更好的解法和獨特的思想(如果有的話)
- 文章中的理解僅為個人理解。如有錯誤,感謝糾錯
🎬個人簡介:努力學習ing
📋本專欄:C++刷題專欄
📋其他專欄:C語言入門基礎,python入門基礎,C++學習筆記,Linux
🎀CSDN主頁 愚潤澤
你可以點擊下方鏈接,進行該專題內不同子專題的學習
| 點擊鏈接 | 開始學習 |
|---|---|
| 雙指針(1) | 雙指針(2) |
| 雙指針(3) | 雙指針(4) |
| 滑動窗口(1) | 滑動窗口(2) |
| 滑動窗口(3) | 滑動窗口(4) |
| 二分查找(1) | 二分查找(2) |
| 前綴和(1) | 前綴和(2) |
| 前綴和(3) | 位運算(1) |
| 位運算(2) | 模擬算法 |
| 快速排序 | 歸并排序 |
| 鏈表 | 哈希表 |
| 字符串 | 棧 |
| 隊列 + 寬搜 | 優先級隊列 |
| BFS 解決 FloodFill | BFS 解決最短路徑 |
| 多源 BFS | BFS 解決拓撲排序 |
題單匯總鏈接:點擊 → 題單匯總(暫時未整理,因為還沒刷完)
題目
- 導論——多源 BFS
- 542. 01 矩陣
- 優質解
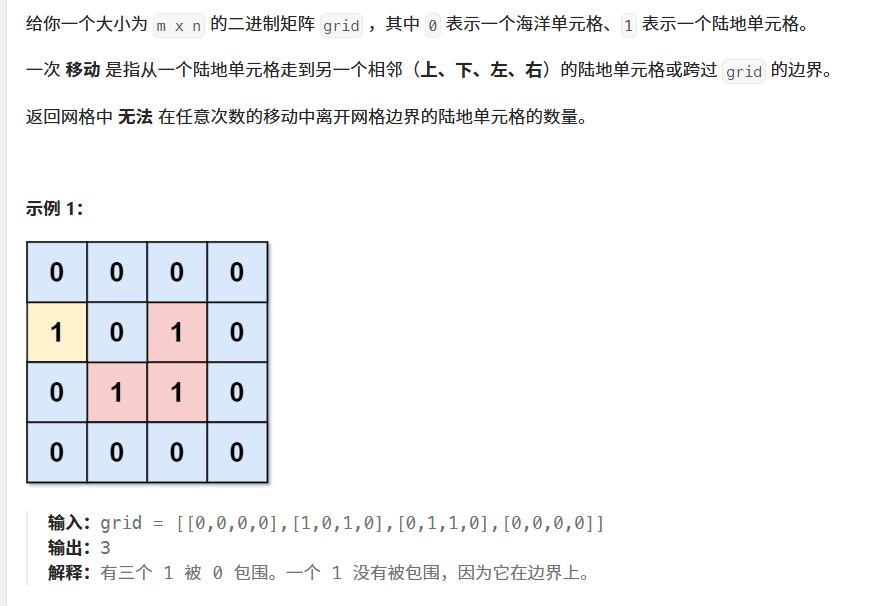
- 1020. 飛地的數量
- 個人解
- 1765. 地圖中的最高點
- 個人解
- 1162. 地圖分析
- 個人解
導論——多源 BFS
多元最短路問題:起始點有多個,去同一個終點
- 前提:BFS解決的最短路問題都是邊權為 1 的
- 解法一:把多源最短路問題轉換成若干個單源最短路問題——暴力枚舉每個起點,對每個起點進行單源最短路問題分析【但是時間復雜度高:超時】
- 解法二:把所有的源點當成一個“超級源點”——從“超級源點”出發,一次單源最短路問題
- 如何求:“超級源點” ?
- 把所有的起始節點加入到隊列中,即:第一層由單源的一個節點變成了多源的多個節點(只不過這些節點都屬于第一層罷了)
- 多個源點可能開辟出不同的路,在不同的路中:后到達的節點會被
hash淘汰
542. 01 矩陣
題目鏈接:https://leetcode.cn/problems/01-matrix/description/

優質解
思路:
- 解法一:把 1 當成起點的話,要遍歷整個矩陣
- 解法二:把 0 當起點:
從所有 0 走到某一個 1 的最短距離 == 從 1 走到最近 0 的距離
代碼:
class Solution {
public:vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m = mat.size(), n = mat[0].size();queue<pair<int, int>> q;vector<vector<int>> dis(m, vector<int>(n, -1));// 先獲得"超級源點"for(int i = 0 ; i < m; i++){for(int j = 0; j < n; j++){if(mat[i][j] == 0){q.push({i, j});dis[i][j] = 0;}}}// 從"超級源點"開始擴展while(q.size()){// int sz = q.size(); 為什么可以不計算 sz ?// 因為之前的 sz 是和 step 配合使用的,我們通過sz知道是在哪一層// 但是現在,下一個dis中填寫的內容可以根據上一個dis中的內容決定// 并且,一定是上一層的節點pop出去以后,才會處理上一層加入的后續節點auto [a, b] = q.front();q.pop();for(int j = 0; j < 4; j++){int x = a + dx[j], y = b + dy[j];if(x >= 0 && x < m && y >= 0 && y < n && dis[x][y] == -1){dis[x][y] = dis[a][b] + 1;q.push({x, y}); }}}return dis;}
};
時間復雜度:O(m?n)O(m*n)O(m?n)
空間復雜度:O(m?n)O(m*n)O(m?n)
1020. 飛地的數量
題目鏈接:https://leetcode.cn/problems/number-of-enclaves/description/
個人解
屎山代碼:
class Solution {
public:int numEnclaves(vector<vector<int>>& grid) {// 這就是 floodfill// 只不過從邊緣 1 開始先標記連通塊的時候可以使用 多源 bfs 標記int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m = grid.size(), n = grid[0].size();queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if((i == 0 || i == m - 1 || j == 0 || j == n - 1) && grid[i][j]){grid[i][j] = 0;q.push({i, j});}}}while(q.size()){auto [a, b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y]){grid[x][y] = 0;q.push({x, y});}}}int ans = 0;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(grid[i][j])ans++;}}return ans;}
};
時間復雜度:O(m?n)O(m*n)O(m?n)
空間復雜度:O(m?n)O(m*n)O(m?n)
1765. 地圖中的最高點
題目鏈接:https://leetcode.cn/problems/map-of-highest-peak/description/

個人解
思路:
- 和 01 矩陣一樣
屎山代碼:
class Solution {
public:vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {// 自行安排出最高高度// 以水域為起點,能到達的最遠的陸地最高(走最短路徑)int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m = isWater.size(), n = isWater[0].size();vector<vector<int>> high(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(isWater[i][j]){q.push({i, j});high[i][j] = 0;}}}while(q.size()){auto [a, b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && high[x][y] == -1){high[x][y] = high[a][b] + 1;q.push({x, y});}}}return high;}
};
時間復雜度:O(m?n)O(m*n)O(m?n)
空間復雜度:O(m?n)O(m*n)O(m?n)
1162. 地圖分析
題目鏈接:https://leetcode.cn/problems/as-far-from-land-as-possible/description/

個人解
思路:
// 海洋到最近的陸地的距離 == 陸地到海洋的最短路徑
// 以陸地為起始點做 bfs
用時:14:00
屎山代碼:
class Solution {
public:int maxDistance(vector<vector<int>>& grid) {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m = grid.size(), n = grid[0].size();queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(grid[i][j])q.push({i, j});}}int ans = 0;while(q.size()){auto [a, b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && !grid[x][y]){grid[x][y] = grid[a][b] + 1;ans = max(ans, grid[x][y]);q.push({x, y});}}}return ans - 1; // 因為第一次是 1 -> 2,但其實是 1}
};
時間復雜度:O(m?n)O(m*n)O(m?n)
空間復雜度:O(m?n)O(m*n)O(m?n)
🌈我的分享也就到此結束啦🌈
要是我的分享也能對你的學習起到幫助,那簡直是太酷啦!
若有不足,還請大家多多指正,我們一起學習交流!
📢公主,王子:點贊👍→收藏?→關注🔍
感謝大家的觀看和支持!祝大家都能得償所愿,天天開心!!!

)

















