一·線性回歸
線性回歸是利用數理統計中回歸分析,來確定兩種或兩種以上變量間相互依賴的定量關系的一種統計分析方法。
相關關系:包含因果關系和平行關系
因果關系:回歸分析【原因引起結果,需要明確自變量和因變量】
平行關系:相關分析【無因果關系,不區分自變量和因變量】
二·一元線性回歸模型理論
一元線性回歸模型表達式為:y=β0?+β1?x+ε
其中:
0.
為模型參數,用于刻畫自變量?x?與因變量?y?線性關系的截距和斜率 。
可以看成y=kx+b中的k而
則可以看看成b
為誤差項,代表除線性因素外,由隨機因素導致的誤差 。
例子:
自變量:工資
因變量:貸款額度
工資到底能產生多大的影響呢?如何比較公平的評定工資的影響呢?
| 工資(x) | 貸款額度(y) |
|---|---|
| 4000 | 10000 |
| 8000 | 12000 |
| 5000 | 8000 |
| 3000 | 10000 |
| 6000 | 15000 |
| 7000 | ? |
三·多元線性回歸模型
多元線性回歸模型:
?y=β0?+β1?x1?+β2?x2?+ε
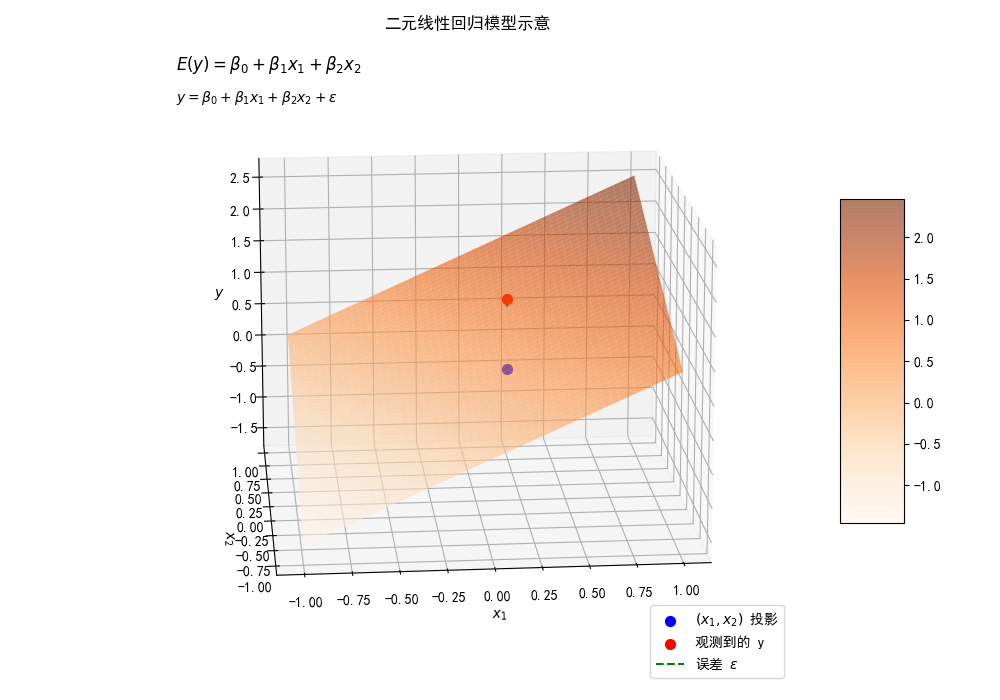
其中:
β0·β1·β2是模型參數。
是誤差項。
誤差項:除線性因素外的隨機因素所產生的誤差。
四·誤差項分析
1. 誤差項可以省略嗎?
答:誤差項不可省略,誤差是必然產生的。并且由于產生了誤差項,我們便可以基于誤差的特點來進行對線性回歸的參數估計的。
2. 誤差項有什么特點?
答:獨立同分布。
獨立:每個樣本點都是獨立的;例:貸款,每個人與每個人之間是沒有聯系的,貸多少錢完全基于你的工資。
同分布:同分布就是我的這套估計體系是我人民銀行的估計體系,每個人都是服從我的分布體系,不會使用別人的估計體系,也就是說每個樣本點都處于同一個分布函數下。
3. 誤差項滿足高斯分布。
高斯分布:
又稱為正態分布,概率密度函數為:
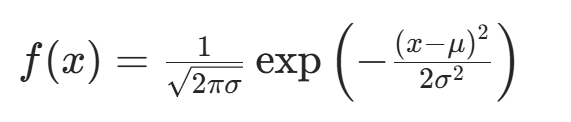
對參數問題的估計就轉化成了對誤差項的分析。
1. 期望為 0;
2. 方差相同,為
控制正態分布圖像的高矮
4·誤差項分析
誤差項分析
線性回歸的轉化:
矩陣計算:
其中x0是1,目的是寫成矩陣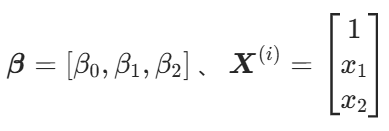
由于為樣本項,為列向量,所以此處對
參數進行轉置,轉為行向量,從而得到以下結果。
?其中T是右上標
矩陣計算——并行化計算?
誤差項分析
預測值與誤差的最終的真實結果:
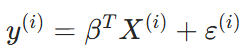
誤差項滿足高斯分布:
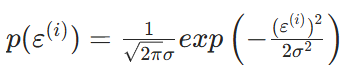
將誤差帶入高斯分布:
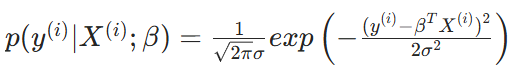
五·極大似然估計
極大似然估計是根據樣本推測參數的方法。核心是找使樣本出現概率最大的參數值,即“最可能”生成該樣本的參數。通過構建似然函數,求其最大值點得到估計,廣泛用于統計推斷。
極大似然估計
假設一個袋子里面有10個球,你抽了一次,發現是黑球;接著又抽了一次,發現又是黑球;在10 次之后,你發現有9次是黑球,1次是白球,那么請問袋子里面黑球有幾個?白球有幾個?
黑球:9/10*10=9個
白球:1/10*10=1個
前提:規律你不知道。 通過事實的數據結果 得到規律
事實發生的事情,一定是最大概率的結果。
六·似然函數求解
似然函數:
一條數據存在一個概率,每條數據都存在這樣一個概率,那么總的概率最大該怎么辦呢?
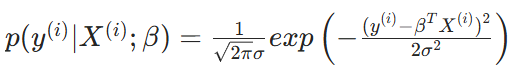
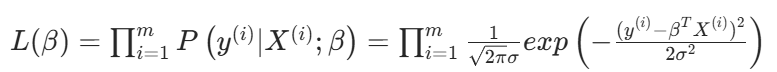
每個樣本都是獨立的,獨立的概率最大,自然是連乘了
似然函數求解
可是連乘不好計算啊,怎么辦呢?
對數似然函數:
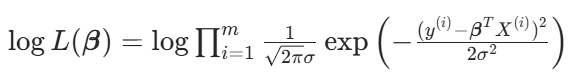
化簡得:
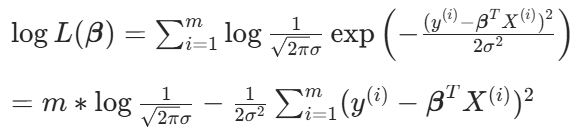
誤差項分析
觀察一下最終計算結果:
?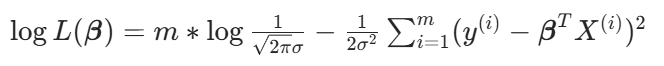
?目標函數:
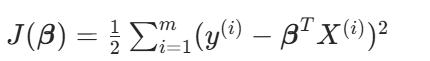
?求式子=0的極小值
最小二乘法求解
目標函數:
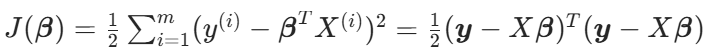
求導結果:
![]()
偏導等于 0:
![]()
?





深度解析:從標準架構到商用實踐)




)





 理論知識)

)
