深度學習（魚書）day08–誤差反向傳播（后三節）

一、激活函數層的實現

這里，我們把構成神經網絡的層實現為一個類。先來實現激活函數的ReLU層和Sigmoid層。

1. ReLU層

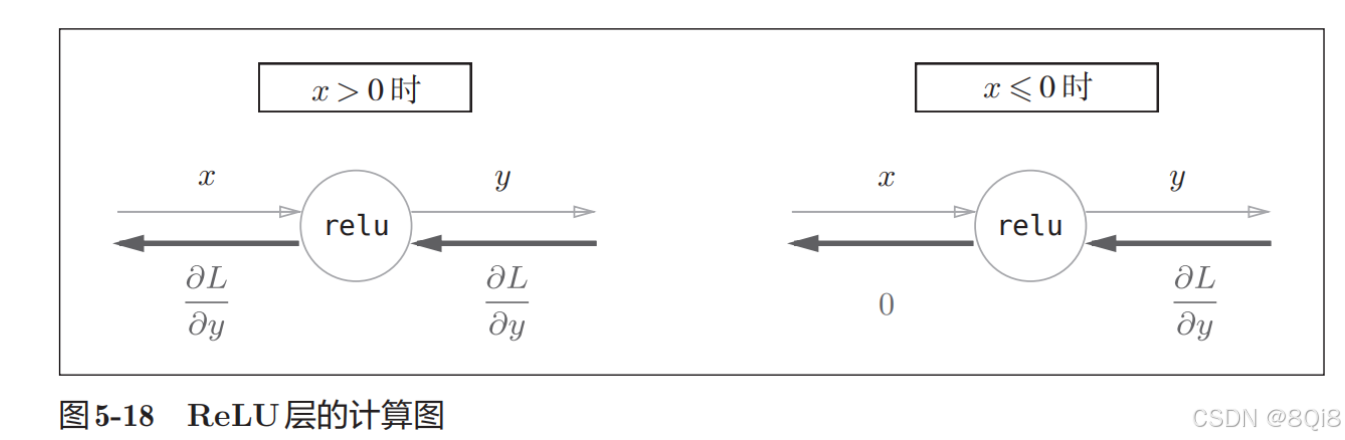
   激活函數ReLU（Rectified Linear Unit）由下式表示。
   $$y=\{\begin{array}{ll}x& (x>0)\\ 0& (x\le 0)\end{array}$$
   y關于x的導數：
   $$\frac{?y}{?x}=\{\begin{array}{ll}1& (x>0)\\ 0& (x\le 0)\end{array}$$
   

   class ReLU:def __init__(self):self.mask = Nonedef forward(self, x):self.mask = (x <= 0)out = x.copy()out[self.mask] = 0def backward(self, dout):dout[self.mask] = 0dx = doutreturn dx
   

   這個變量mask是由True/False構成的NumPy數組，它會把正向傳播時的輸入x的元素中小于等于0的地方保存為True，其他地方（大于0的元素）保存為False。

   如果正向傳播時的輸入值小于等于0，則反向傳播的值為0。因此，反向傳播中會使用正向傳播時保存的mask，將從上游傳來的dout的mask中的元素為True的地方設為0。

   ReLU層的作用就像電路中的開關一樣。正向傳播時，有電流通過的話，就將開關設為 ON；沒有電流通過的話，就將開關設為 OFF。反向傳播時，開關為ON的話，電流會直接通過；開關為OFF的話，則不會有電流通過。

2. Sigmoid層

   

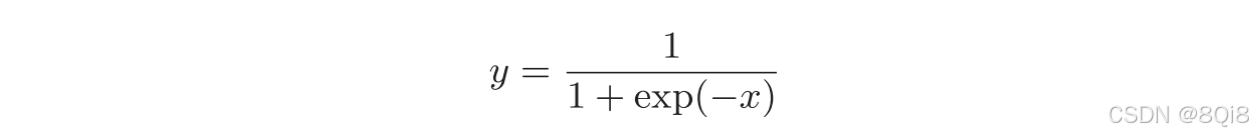
   正向傳播：

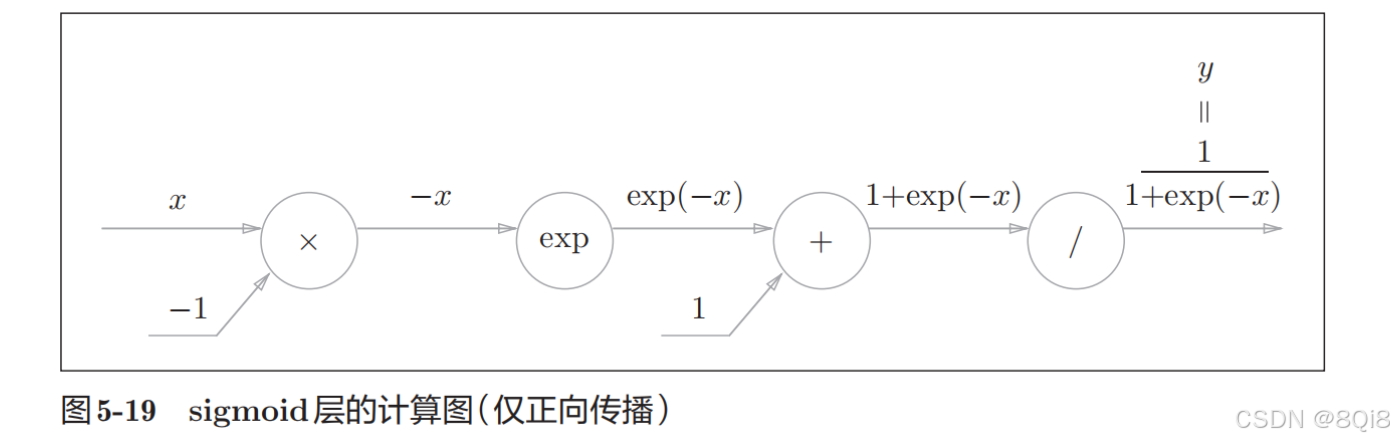
反向傳播：

步驟1

“/”節點表示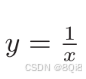
，它的導數可以解析性地表示為下式。

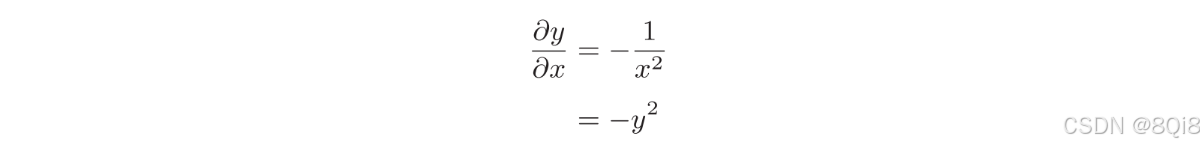
反向傳播時，會將上游的值乘以-y 2 （正向傳播的輸出的平方乘以?1后的值）后，再傳給下游。計算圖如下所示。

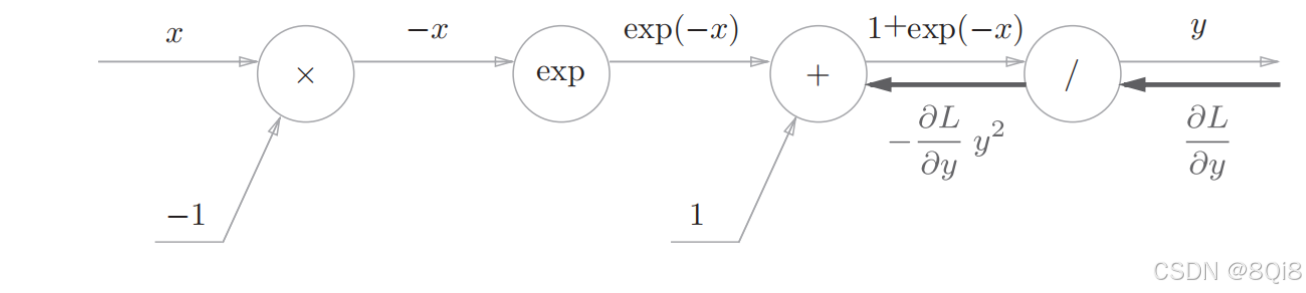
步驟2

“+”節點將上游的值原封不動地傳給下游。計算圖如下所示。

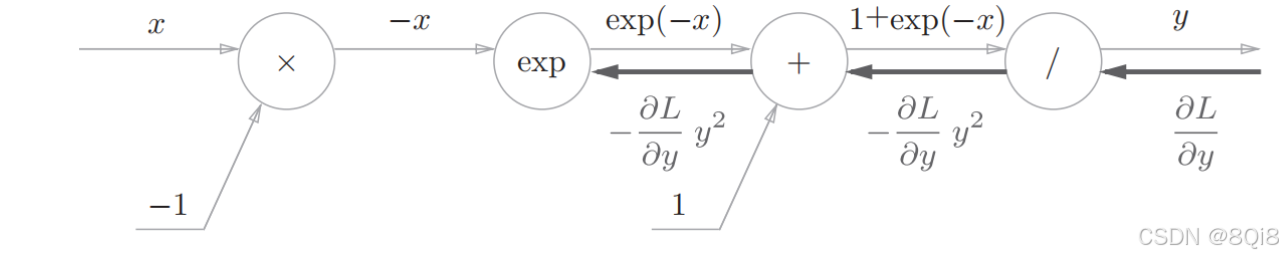
步驟3

“exp”節點表示y = exp(x)，它的導數由下式表示。

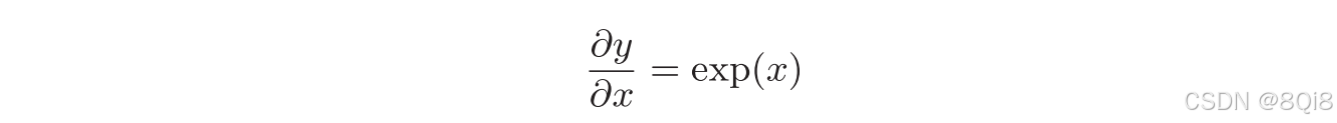
上游的值乘以正向傳播時的輸出（這個例子中是exp(?x)）后，再傳給下游。

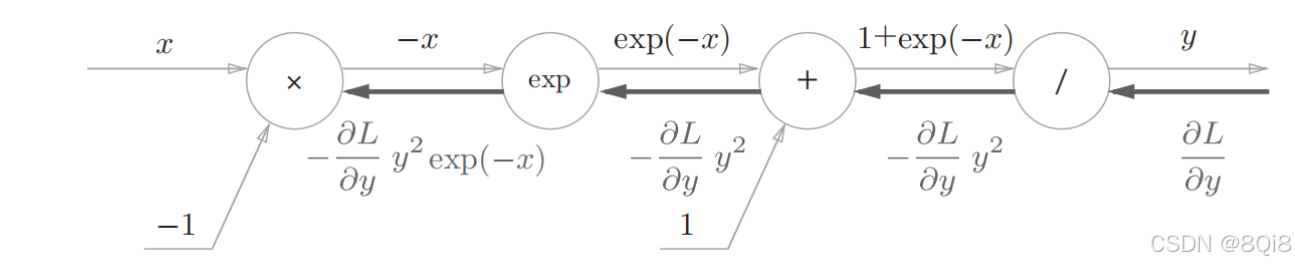
步驟4

“×”節點將正向傳播時的值翻轉后做乘法運算。因此，這里要乘以?1。

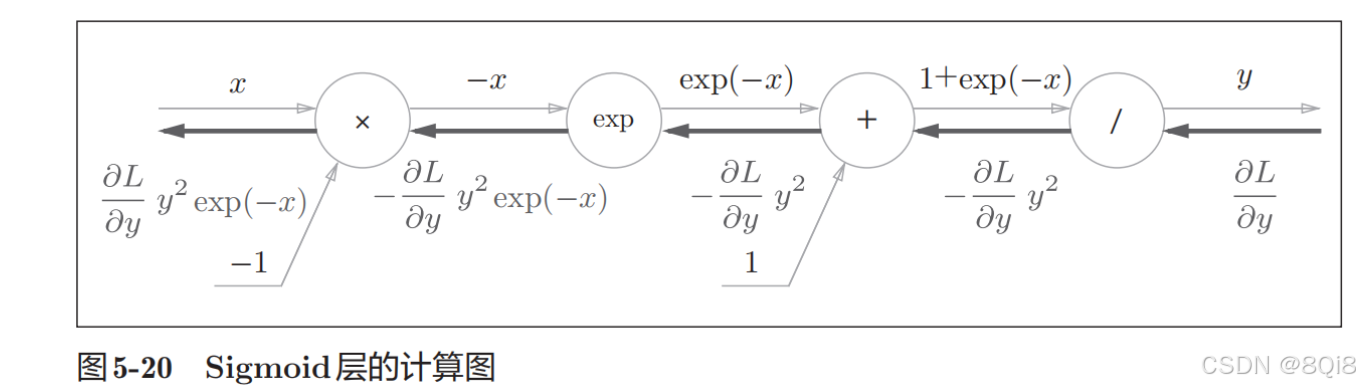
集約化的“sigmoid”節點。可以不用在意Sigmoid層中瑣碎的細節，而只需要專注它的輸入和輸出，這一點也很重要。

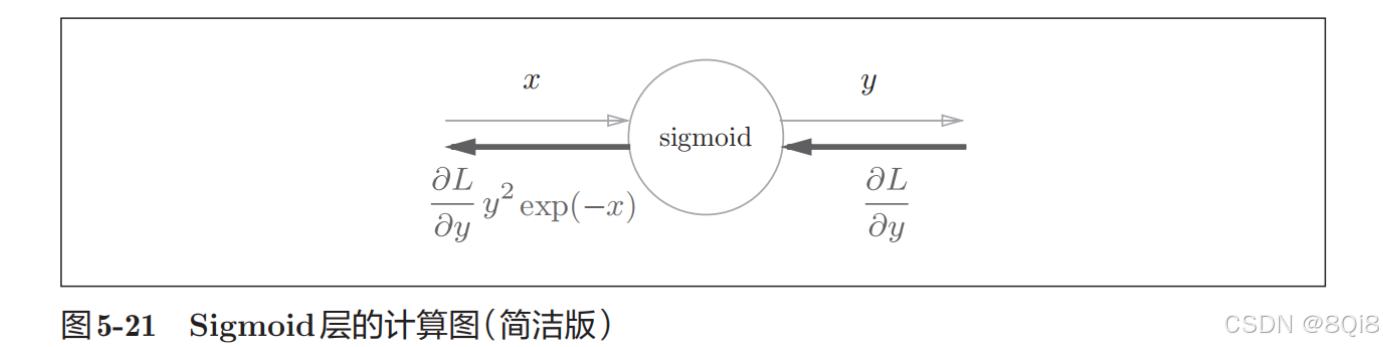
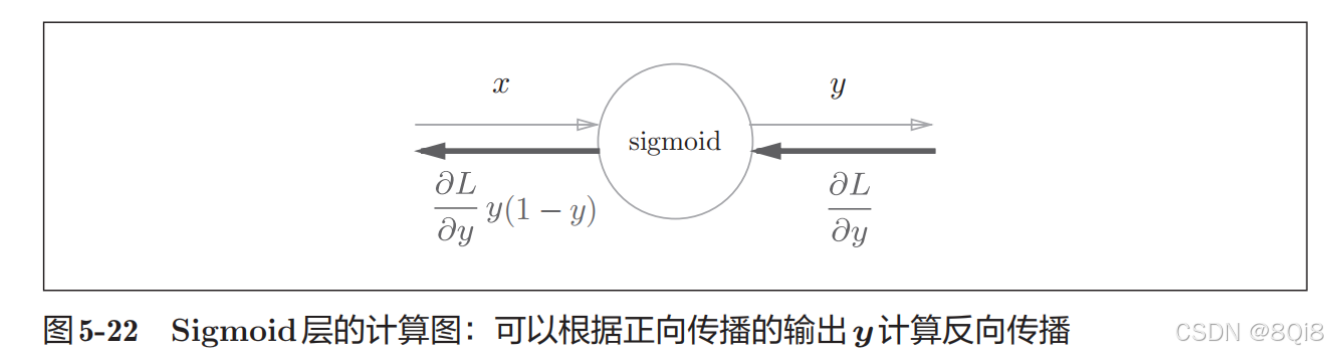
進一步整理如下：

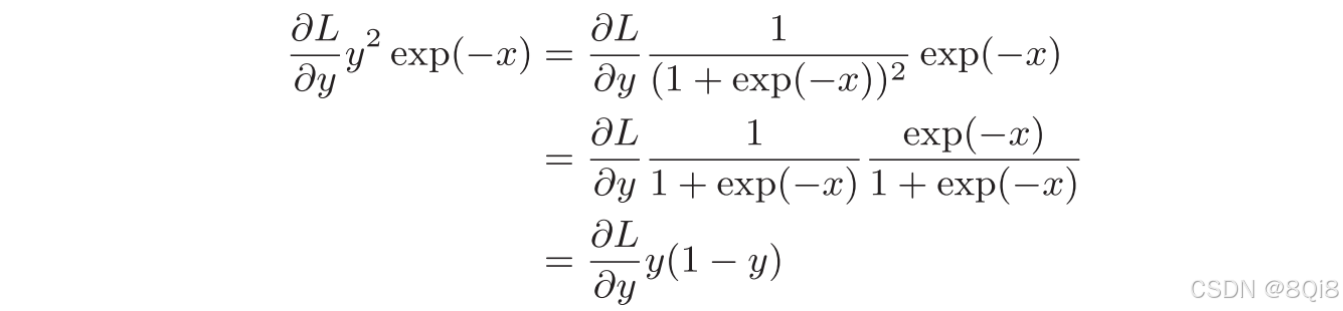
因此，Sigmoid層的反向傳播，只根據正向傳播的輸出就能計算出來。

代碼實現：

class Sigmoid:def __init__(self):self.out = Nonedef forward(self, x):out = 1 / (1 + np.exp(-x))self.out = outreturn outdef backward(self, dout):dx = dout * (1.0 - self.out) * self.outreturn dx

二、Affine/Softmax層的實現

1. Affine層

   神經網絡的正向傳播中進行的矩陣乘積運算在幾何學領域被稱為“仿射變換”。因此，這里將進行仿射變換的處理實現為“Affine層”。

   現在將這里進行的求矩陣的乘積與偏置的和的運算用計算圖表示出來。將乘積運算用“dot”節點表示的話，則np.dot(X, W) + B的運算可用下圖所示的計算圖表示出來。在各個變量的上方標記了它們的形狀（計算圖上顯示了X的形狀為(2,)，X·W的形狀為(3,)）。

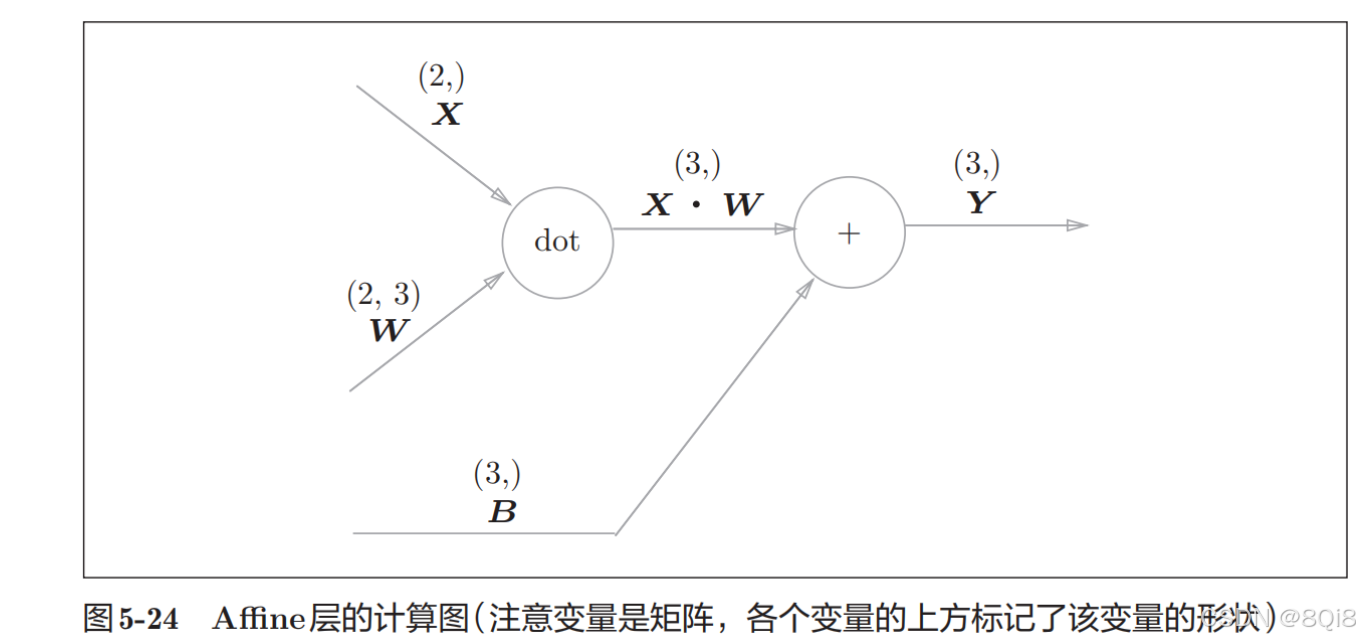
現在我們來考慮圖5-24的計算圖的反向傳播。以矩陣為對象的反向傳播，按矩陣的各個元素進行計算時，步驟和以標量為對象的計算圖相同。實際寫一下的話，可以得到下式：

嘗試寫出計算圖的反向傳播，如圖所示：

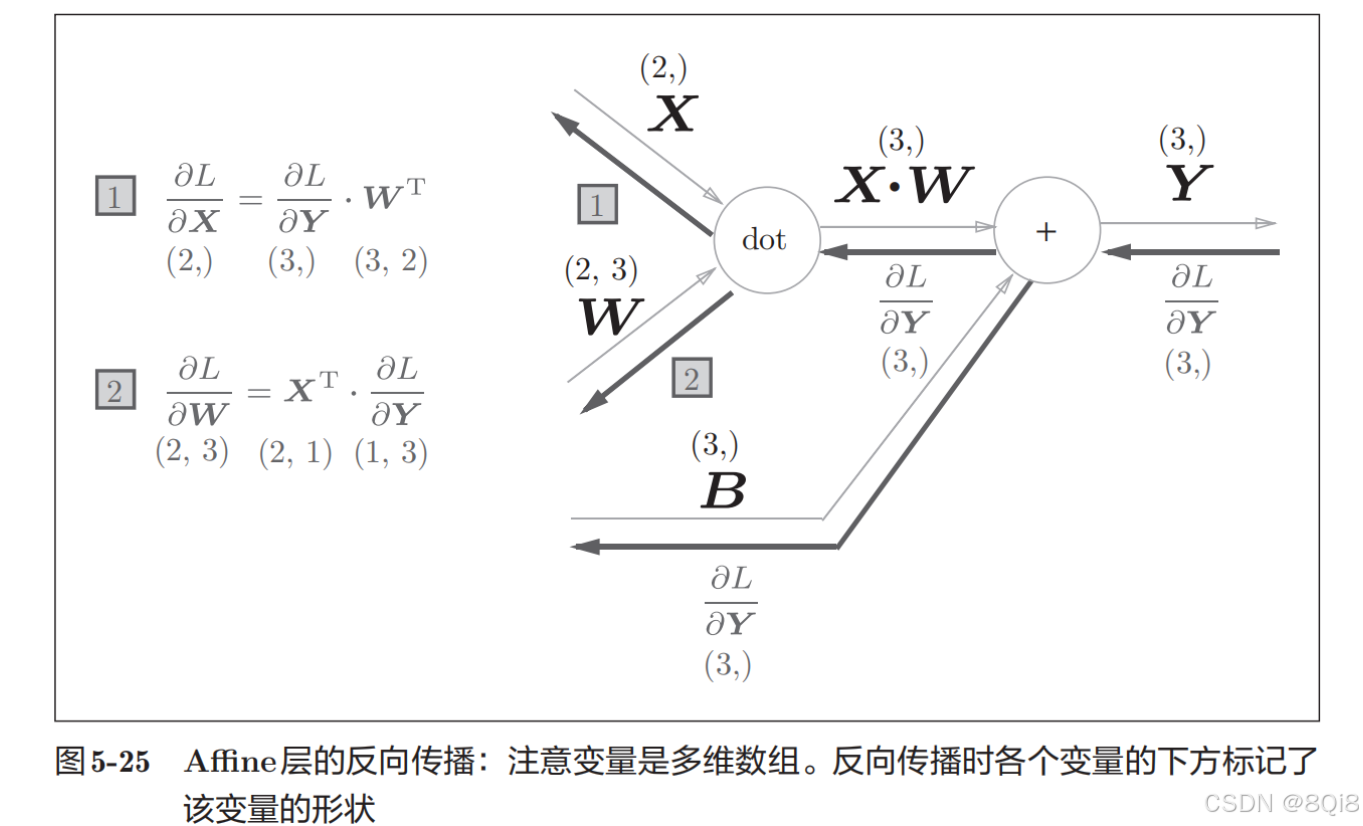
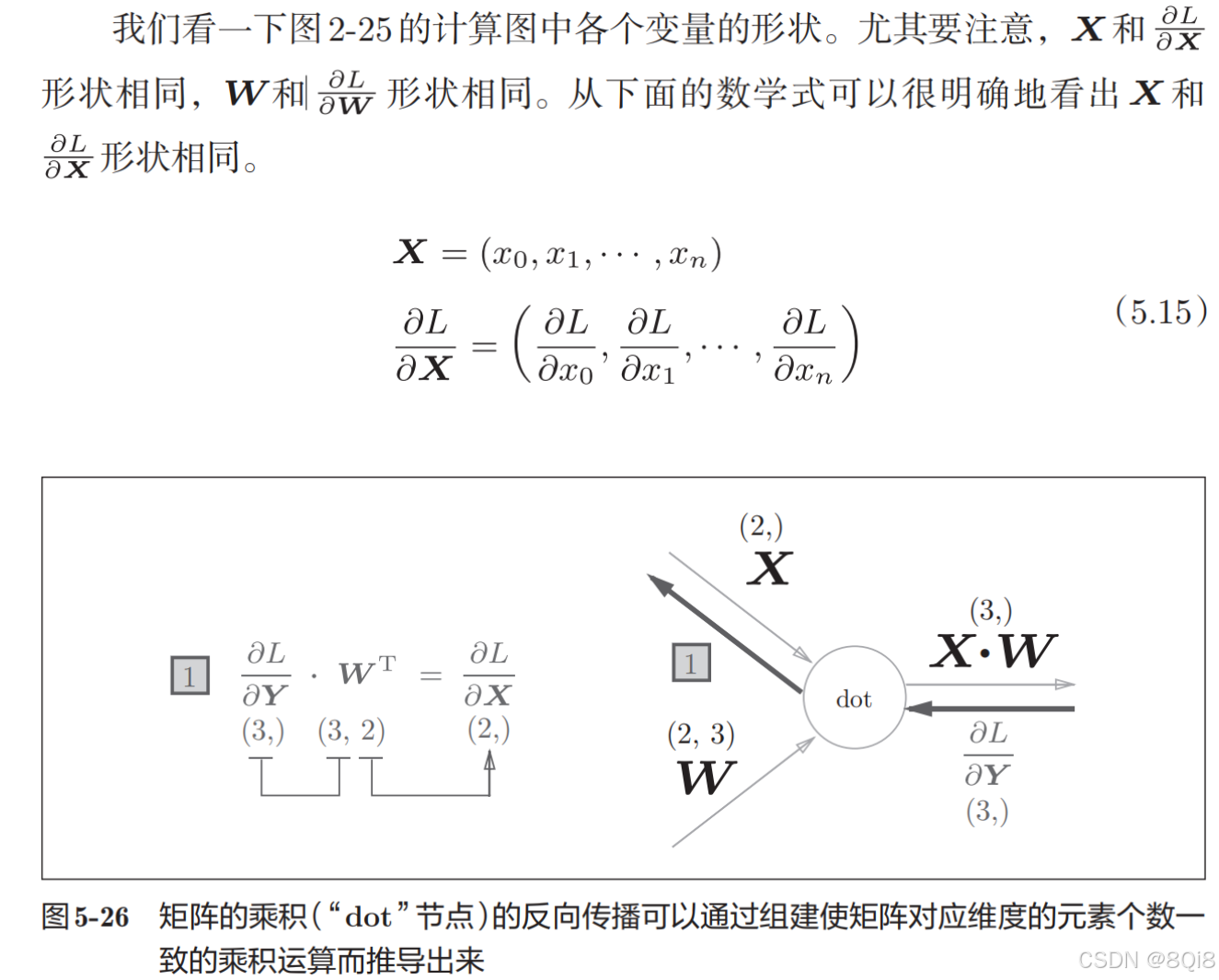
2. 批版本的Affine層

   前面介紹的Affi ne層的輸入X是以單個數據為對象的。現在我們考慮N個數據一起進行正向傳播的情況，也就是批版本的Affine層。先給出批版本的Affine層的計算圖，如圖所示。

   

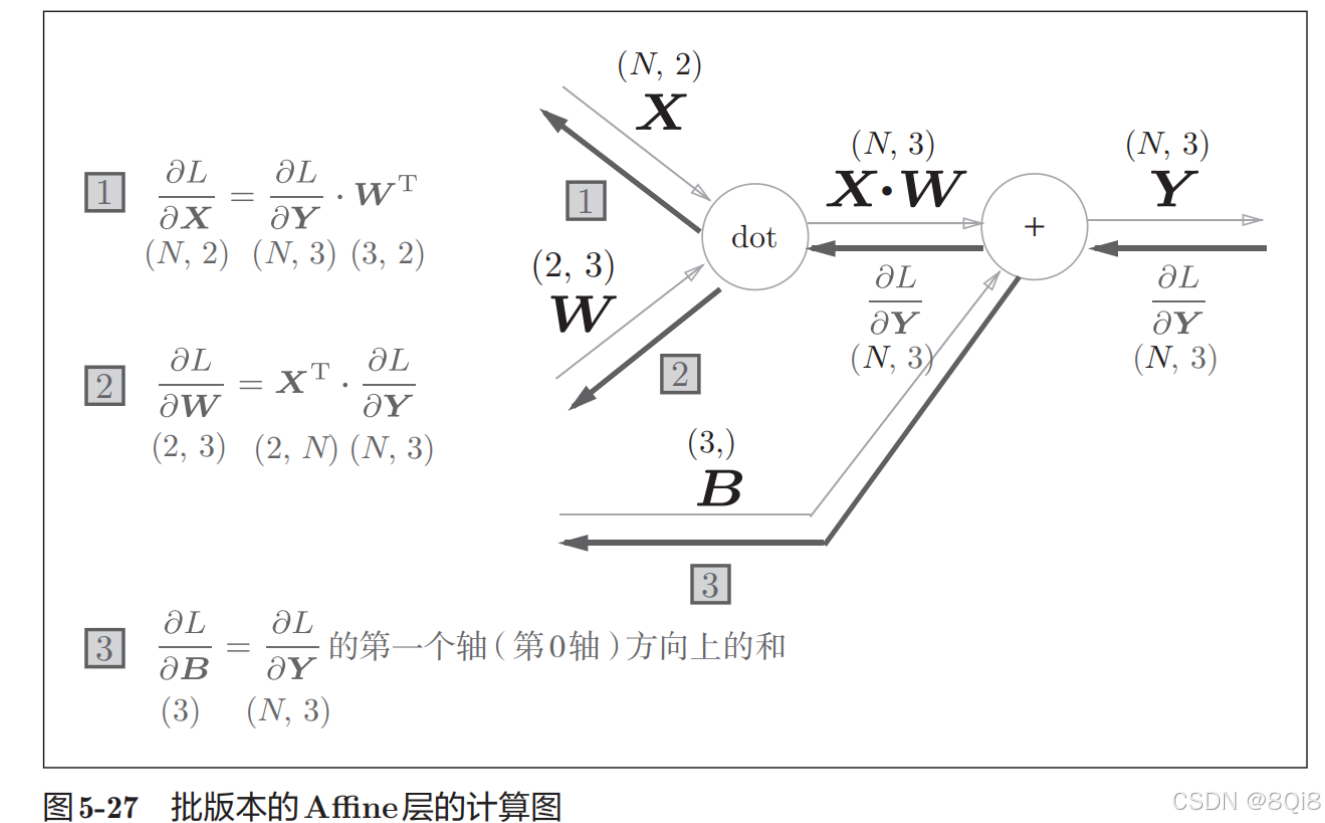
   正向傳播時，偏置會被加到每一個數據（第1個、第2個……）上。因此，反向傳播時，各個數據的反向傳播的值需要匯總為偏置的元素。用代碼表示的話，如下所示。

這里使用了np.sum()對第0軸（以數據為單位的軸，axis=0）方向上的元素進行求和。

class Affine:def __init__(self, W, b):self.W =Wself.b = bself.x = Noneself.dW = Noneself.db = Nonedef forward(self, x):self.x = xout = np.dot(x, self.W) + self.breturn outdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)return dx

輸入數據為張量（四維數據）的情況:

class Affine:def __init__(self, W, b):self.W =Wself.b = bself.x = Noneself.original_x_shape = None# 權重和偏置參數的導數self.dW = Noneself.db = Nonedef forward(self, x):# 對應張量self.original_x_shape = x.shapex = x.reshape(x.shape[0], -1)self.x = xout = np.dot(self.x, self.W) + self.breturn outdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)dx = dx.reshape(*self.original_x_shape)  # 還原輸入數據的形狀（對應張量）return dx

3. Softmax-with-Loss 層

   softmax函數會將輸入值正規化之后再輸出。比如手寫數字識別時，Softmax層的輸出如圖所示。

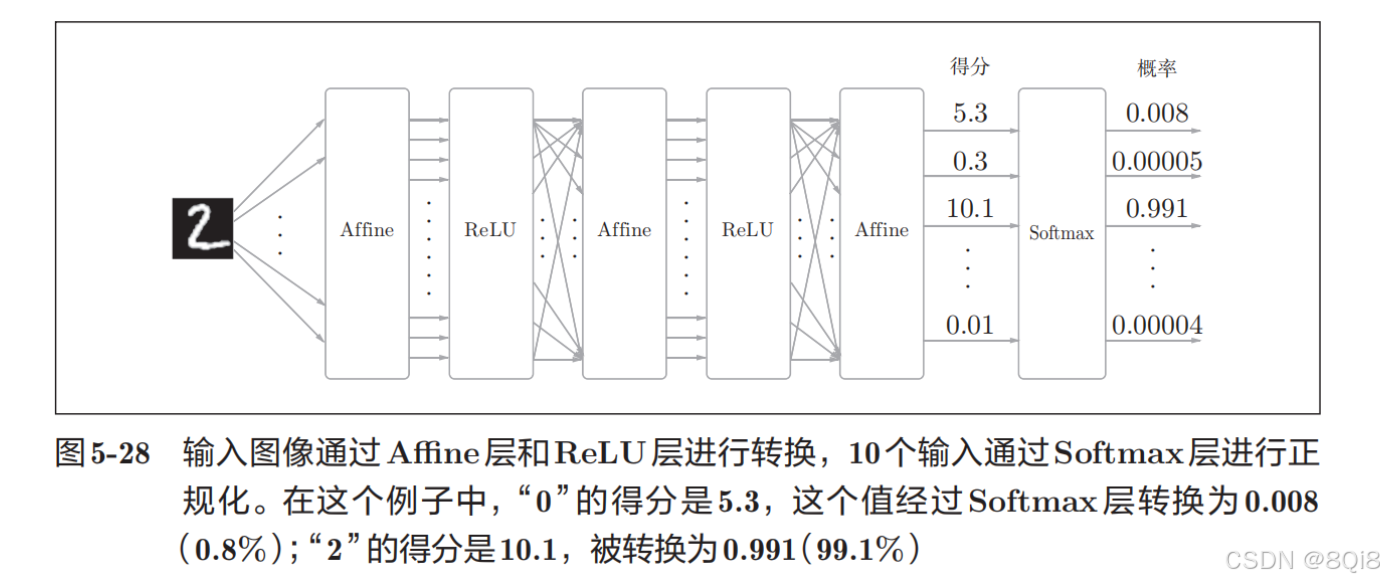
神經網絡中進行的處理有推理（inference）和學習兩個階段。神經網絡的推理通常不使用 Softmax層。比如，用圖 5-28的網絡進行推理時，會將最后一個 Affine層的輸出作為識別結果。神經網絡中未被正規化的輸出結果有時被稱為“得分”。也就是說，當神經網絡的推理只需要給出一個答案的情況下，因為此時只對得分最大值感興趣，所以不需要 Softmax層。不過，神經網絡的學習階段則需要 Softmax層。

這里也包含作為損失函數的交叉熵誤差（cross entropy error），所以稱為“Softmax-with-Loss層”。Softmax-with-Loss層（Softmax函數和交叉熵誤差）的計算圖如圖所示。

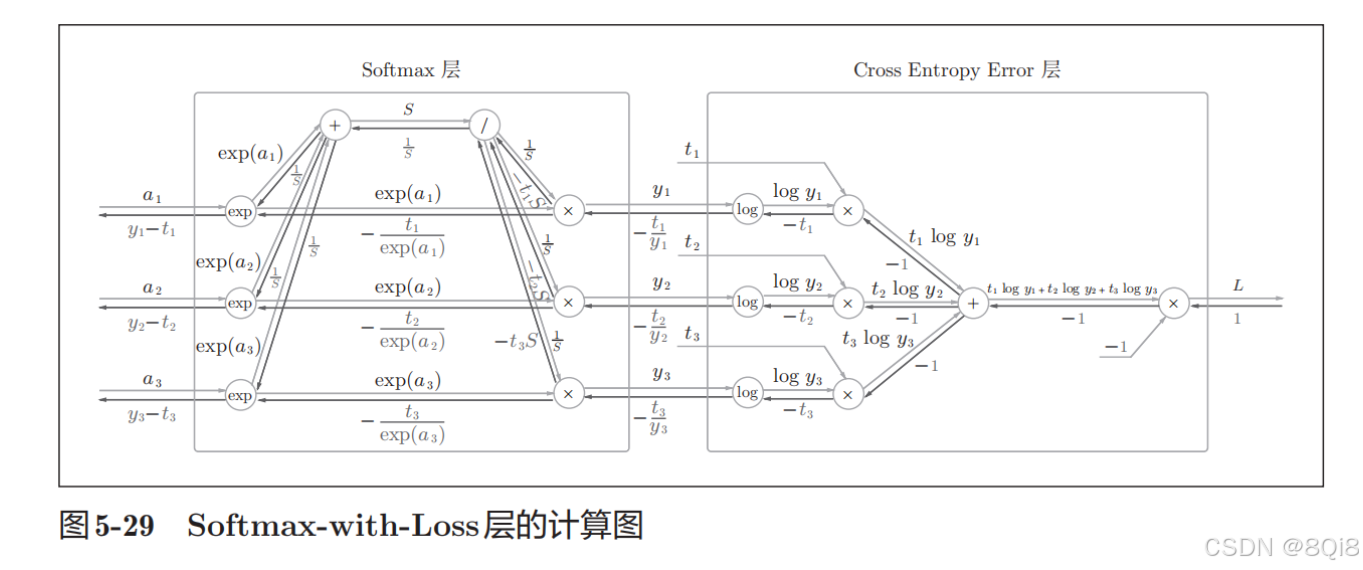
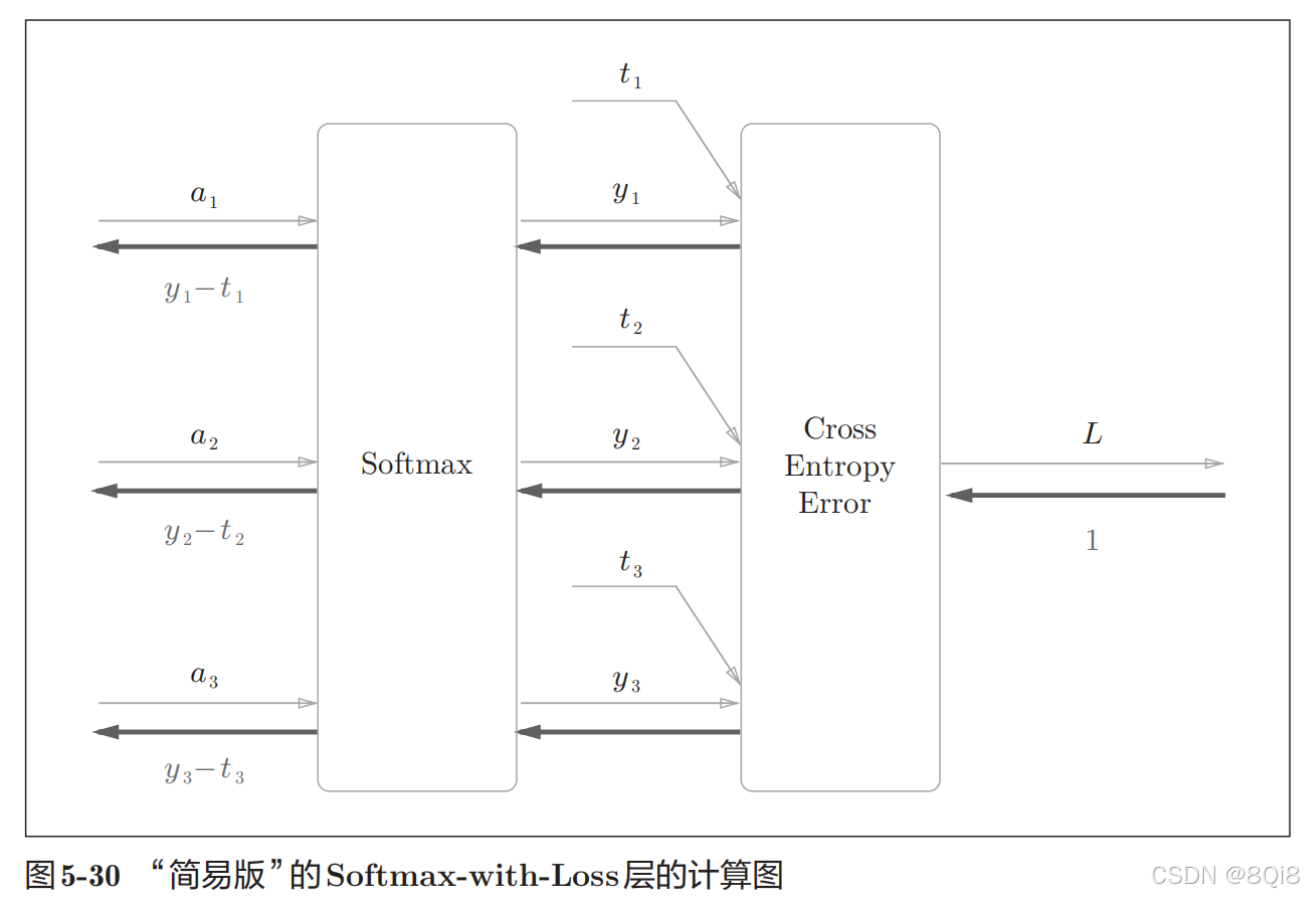
• 這里假設要進行3類分類，從前面的層接收3個輸入（得分）。Softmax層將輸入（a1, a2, a3）正規化，輸出（y1, y2, y3）。Cross Entropy Error層接收Softmax的輸出（y1, y2, y3）和教師標簽（t1, t2, t3），從這些數據中輸出損失L。

• 注意反向傳播的結果：Softmax層的反向傳播得到了（y1 ? t1, y2 ? t2, y3 ? t3）這樣“漂亮”的結果。由于（y1, y2, y3）是Softmax層的輸出，（t1, t2, t3）是監督數據，所以（y1 ? t1, y2 ? t2, y3 ? t3）是Softmax層的輸出和教師標簽的差分。神經網絡的反向傳播會把這個差分表示的誤差傳遞給前面的層，這是神經網絡學習中的重要性質。

• 考慮一個具體的例子，比如教師標簽是 （0, 1, 0），Softmax層的輸出是 (0.3, 0.2, 0.5)的情形。因為正確解標簽處的概率是0.2（20%），這個時候的神經網絡未能進行正確的識別。此時，Softmax層的反向傳播傳遞的是(0.3, ?0.8, 0.5)這樣一個大的誤差。因為這個大的誤差會向前面的層傳播，所以Softmax層前面的層會從這個大的誤差中學習到“大”的內容。

• 回歸問題中輸出層使用“恒等函數”，損失函數使用“平方和誤差”，也是出于同樣的理由。也就是說，使用“平方和誤差”作為“恒等函數”的損失函數，反向傳播才能得到（y1 ?t1, y2 ? t2, y3 ? t3）這樣“漂亮”的結果。

• 再舉一個例子，比如思考教師標簽是 (0, 1, 0)，Softmax層的輸出是 (0.01, 0.99, 0)的情形（這個神經網絡識別得相當準確）。此時Softmax層的反向傳播傳遞的是 (0.01, ?0.01, 0)這樣一個小的誤差。這個小的誤差也會向前面的層傳播，因為誤差很小，所以Softmax層前面的層學到的內容也很“小”。

Softmax-with-Loss層的實現：

class SoftmaxWithLoss:def __init__(self):self.loss = Noneself.y = Noneself.t = Nonedef forward(self, x, t):self.t = tself.y = softmax(x)self.loss = cross_entropy_error(self.y, self.t)return self.lossdef backward(self, dout=1):batch_size = self.t.shape[0]if self.t.size == self.y.size:  # 監督數據是one-hot-vector的情況dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx

注意反向傳播時，將要傳播的值除以批的大小（batch_size）后，傳遞給前面的層的是單個數據的誤差。

三、誤差反向傳播法的實現

通過像組裝樂高積木一樣組裝上一節中實現的層，可以構建神經網絡。本節我們將通過組裝已經實現的層來構建神經網絡。

1. 神經網絡學習的全貌圖

步驟2中，之前我們利用數值微分求得了這個梯度。數值微分雖然實現簡單，但是計算要耗費較多的時間。和需要花費較多時間的數值微分不同，誤差反向傳播法可以快速高效地計算梯度。

2. 對應誤差反向傳播法的神經網絡的實現

   import sys, os
   sys.path.append(os.pardir)  # 為了導入父目錄的文件而進行的設定
   import numpy as np
   from common.layers import *
   from common.gradient import numerical_gradient
   from collections import OrderedDictclass TwoLayerNet:def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):# 初始化權重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)self.params['b1'] = np.zeros(hidden_size)self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size)# 生成層self.layers = OrderedDict()self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])self.layers['Relu1'] = Relu()self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])self.lastLayer = SoftmaxWithLoss()def predict(self, x):for layer in self.layers.values():x = layer.forward(x)return x# x:輸入數據, t:監督數據def loss(self, x, t):y = self.predict(x)return self.lastLayer.forward(y, t)def accuracy(self, x, t):y = self.predict(x)y = np.argmax(y, axis=1)if t.ndim != 1 : t = np.argmax(t, axis=1)accuracy = np.sum(y == t) / float(x.shape[0])return accuracy# x:輸入數據, t:監督數據def numerical_gradient(self, x, t):loss_W = lambda W: self.loss(x, t)grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])return gradsdef gradient(self, x, t):# forwardself.loss(x, t)# backwarddout = 1dout = self.lastLayer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:dout = layer.backward(dout)# 設定grads = {}grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn grads
   

OrderedDict是有序字典，“有序”是指它可以記住向字典里添加元素的順序。因此，神經網絡的正向傳播只需按照添加元素的順序調用各層的forward()方法就可以完成處理，而反向傳播只需要按照相反的順序調用各層即可。因為Affine層和ReLU層的內部會正確處理正向傳播和反向傳播，所以這里要做的事情僅僅是以正確的順序連接各層，再按順序（或者逆序）調用各層。

3. 誤差反向傳播法的梯度確認
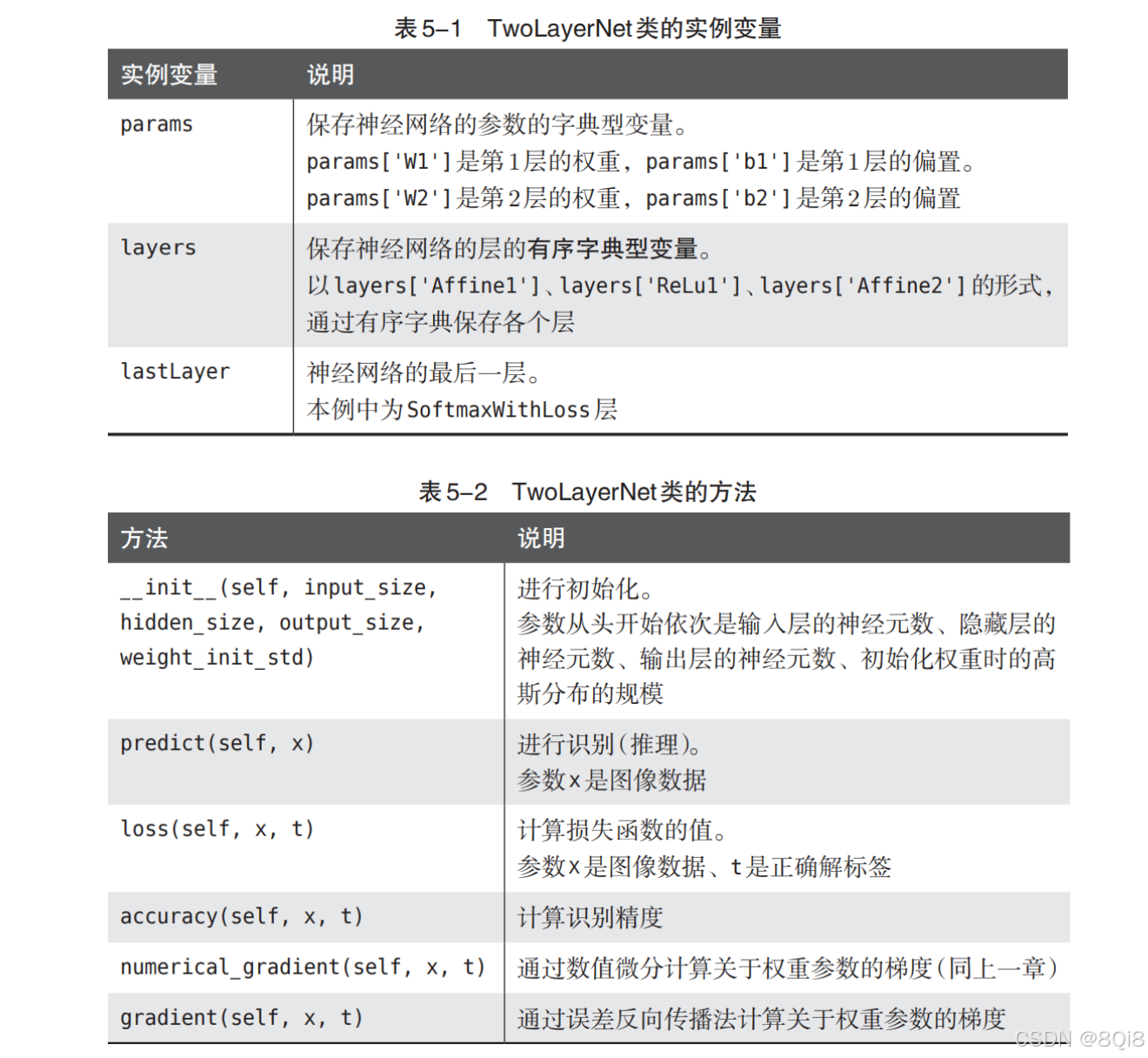
   在確認誤差反向傳播法的實現是否正確時，是需要用到數值微分的。數值微分的優點是實現簡單，一般情況下不太容易出錯。而誤差反向傳播法的實現很復雜，容易出錯。所以，經常會比較數值微分的結果和誤差反向傳播法的結果，以確認誤差反向傳播法的實現是否正確。確認數值微分求出的梯度結果和誤差反向傳播法求出的結果是否一致（嚴格地講，是非常相近）的操作稱為梯度確認（gradient check）。

   import sys, os
   sys.path.append(os.pardir)  # 為了導入父目錄的文件而進行的設定
   import numpy as np
   from dataset.mnist import load_mnist
   from two_layer_net import TwoLayerNet# 讀入數據
   (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)x_batch = x_train[:3]
   t_batch = t_train[:3]grad_numerical = network.numerical_gradient(x_batch, t_batch)
   grad_backprop = network.gradient(x_batch, t_batch)for key in grad_numerical.keys():diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )print(key + ":" + str(diff))
   

通過數值微分和誤差反向傳播法求出的梯度的差非常小。所以誤差反向傳播法求出的梯度是正確的。

2. 使用誤差反向傳播法的學習

   和之前的實現相比，不同之處僅在于通過誤差反向傳播法求梯度這一點。

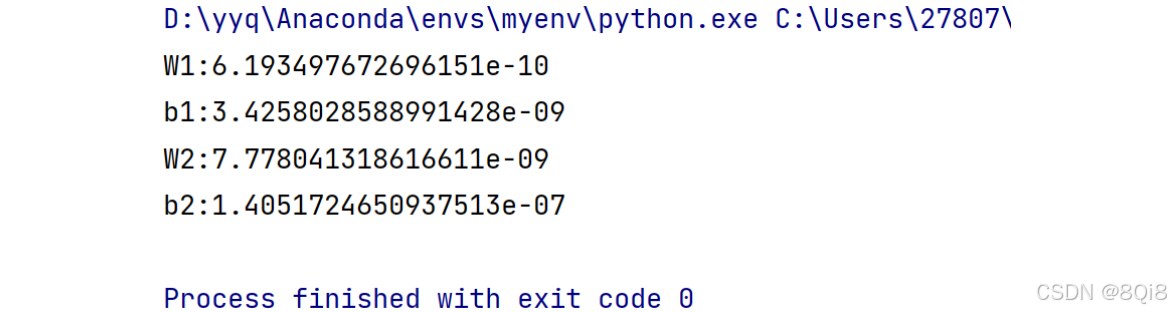
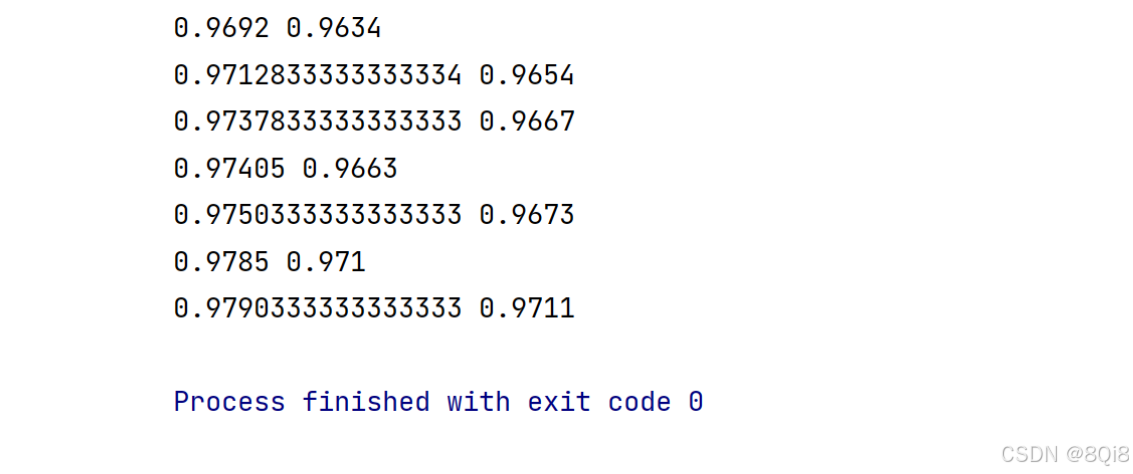
   # coding: utf-8
   import sys, os
   sys.path.append(os.pardir)import numpy as np
   from dataset.mnist import load_mnist
   from two_layer_net import TwoLayerNet# 讀入數據
   (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)iters_num = 10000
   train_size = x_train.shape[0]
   batch_size = 100
   learning_rate = 0.1train_loss_list = []
   train_acc_list = []
   test_acc_list = []iter_per_epoch = max(train_size / batch_size, 1)for i in range(iters_num):batch_mask = np.random.choice(train_size, batch_size)x_batch = x_train[batch_mask]t_batch = t_train[batch_mask]# 梯度#grad = network.numerical_gradient(x_batch, t_batch)grad = network.gradient(x_batch, t_batch)# 更新for key in ('W1', 'b1', 'W2', 'b2'):network.params[key] -= learning_rate * grad[key]loss = network.loss(x_batch, t_batch)train_loss_list.append(loss)if i % iter_per_epoch == 0:train_acc = network.accuracy(x_train, t_train)test_acc = network.accuracy(x_test, t_test)train_acc_list.append(train_acc)test_acc_list.append(test_acc)print(train_acc, test_acc)