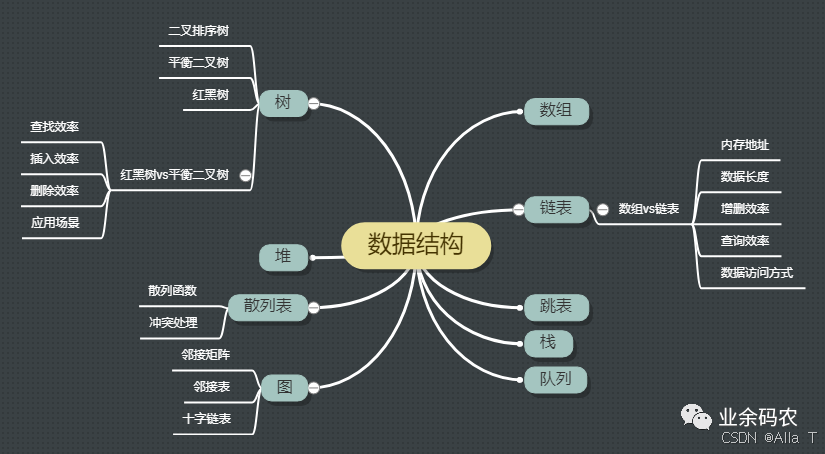
數據結構=邏輯結構+物理結構(存儲結構),數據結構是計算機中存儲、組織數據的方式。
其中物理結構是數據的邏輯結構在計算機中的存儲形式。而存儲器針對內存而言,像硬盤、軟盤、光盤等外部存儲器的數據組織常用文件結構描述。
1. 基礎算法
1.1 遞歸Recursion
- 函數在定義中使用函數自身的方法,例子是求斐波那契數列。
long long Fib(int i) {if(i<=1) return i;return Fib(i-1)+Fib(i-2); }
1.2 分治Divide and Conquer
分治,即分而治之。?將大問題分成幾個小部分計算,最后再將小部分結果合并起來
- 要考慮什么時候是基礎情況,很多時候依靠遞歸實現
int RecSum(int l, int r) {int mid = l + r >> 1; // 因為這里是位運算,相當于整數除以2;該寫法常見于二分查找、分治算法等腰計算中間值return RecSum(l,mid)+RecSum(mid+l, r);
}
這段代碼是遞歸求和函數,但因為沒有終止條件會導致無限遞歸和棧溢出(stack overflow)。即沒有處理l==r的情況,修正后
int RecSum(int l, int r) {if (l==r) return l;int mid =
}
1.3 貪心算法
- 基本思想
1)求解最優化問題的算法包含一系列步驟
2)每一步都有一組選擇
3)做出當前最好的選擇
4)通過局部最優選擇達到全局最優-> 未必達到全局最優
5)是否能達到最優解需嚴格證明 - 產生最優解的條件
1)最優子結構:
2)貪心選擇性:
2. 線性表
數據的存儲結構應正確反映數據元素間的邏輯關系
體現為線性表的順序存儲能用數據實現,而元素物理
1)個數有限;2)元素有先后次序;3)數據類型相同;4)討論元素間的邏輯關系
一旦數據被線性表存儲,在邏輯上的相對位置就固定下來了。線性表分為順序表和鏈表。其中鏈式存儲允許存儲空間不連續,但順序表不行。
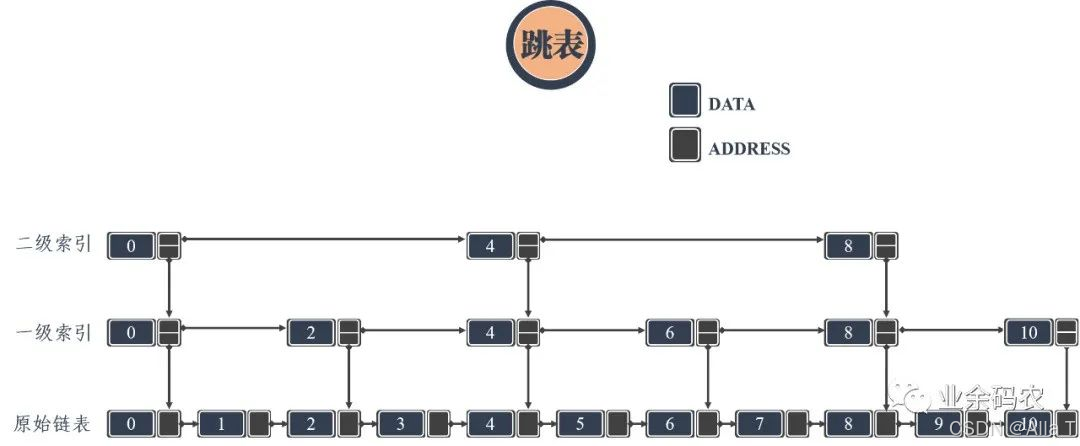
2.1 跳表
上面的對比中可以看出,鏈表雖然通過增加指針域提升了自由度,但是卻導致數據的查詢效率惡化。特別是當鏈表長度很長的時候,對數據的查詢還得從頭依次查詢,這樣的效率會更低。跳表的產生就是為了解決鏈表過長的問題,通過增加鏈表的多級索引來加快原始鏈表的查詢效率。這樣的方式可以讓查詢的時間復雜度從O(n)提升至O(logn)。
1)
2)
3)
3. 棧
3.1 棧
遵守LIFO原則(后進先出)
3.2 隊列
遵守FIFO原則(先進先出)
4. 樹
4.1 二叉樹(Binary Tree)
- 特點:除了最后一層外,其他層節點必須完全填滿(每層從左到右沒有空缺),最后一層的節點必須連續集中在左側(允許右側有空缺但左側不能有)
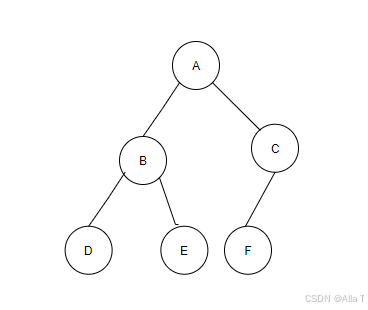
- 二叉樹代碼
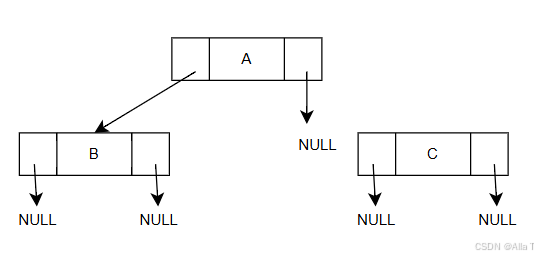
此處是鏈式存儲typedef struct BiNode {char data;struct BiTNode *lchild, *rchild; // 左右孩子指針 } BiTNode, *BiTree; BiTree root = NULL; // 根節點 root = (BiTree)malloc(sizeof(BiTNode)); root -> data = 'A'; root -> lchild = NULL; root -> rchild = NULL; // 插入結點B BiTNode *BNode = NULL; BNode = (BiTNode*)malloc(sizeof(BiTNode)); BNode->data = 'B'; BNode->lchild = NULL; BNode->rchild = NULL; root->lchild = BNode; // 定義了B之后才將A對應的root的左子樹連接到B中 // 插入結點C BiTNode *CNode = NULL; CNode = (BiTNode*)malloc(sizeof(BiTNode)); CNode -> data = 'C'; CNode -> lchild = NULL; CNode -> rchild = NULL; root -> rchild = CNode; - 二叉樹
4.2 B+樹
MySQL InnoDB索引(B+樹)作為主要的索引結構,用于主鍵索引(聚簇索引)和輔助索引(二級索引)。B+樹相比于AVL樹、紅黑樹等數據結構,更適合數據庫的大規模數據存儲和磁盤存取優化。
-
B+:平衡樹(非二叉樹),具有以下特點
1)每個B+樹的結點中含有n個關鍵字,而B+樹每個節點中關鍵字個數n的取值范圍是?m/2?≤n≤m?m/2?≤n≤m?m/2?≤n≤m
2)所有的葉子節點包含了關鍵字的信息,及指向關鍵字記錄的指針,且葉子節點本身依關鍵字的大小自小而大順序鏈接。
3)所有非終端節點(非葉子)是索引,結點中僅含有其子樹(根節點)中最大/小的關鍵字 -
1
-
1
4.3 AVL樹
4.4
5. 圖
5.1 圖的
6. 哈希表
- 概念:哈希表指通過哈希函數將鍵值映射到值的數據結構
- 哈希沖突:通過哈希查找發現該位置上已有對應的關鍵碼值,發生沖突
- 解決沖突的方法:
1)開發地址法:尋找另一個空閑地址,包括線性探測法和平方探測法
2)鏈地址法:將所有哈希地址相同的記錄鏈接到同一鏈表中,適用于頻繁插入刪除
3)再哈希法:使用其他哈希函數計算新的地址 - 相關的代碼
// 兩數之和:給定一個整數數組nums和整數目標值target,請在該數組中找出和為目標值target的兩個整數,并返回數組下標
class Solution {
public: vector<int> twoSum(vector<int>& nums, int target) {vector<int> ret;}
}6.1
7. 堆
用于動態內存管理
7.1
8. 動態規劃
將會定義兩個關鍵:一是動態規劃,二是狀態轉移。
其中狀態定義是把求解過程中所有狀態(子問題)表示出來是動態規劃的難點
8.1 區間dp和樹形dp
8.2
8.3 常見問題
- 樸素區間dp:在區間上進行dp,主要思路是通過合并小區間得到大區間的最優解
大區間是cost[i][j][k],其中包含dp[i][j]和dp[j][k],將其合并為區間dp[i][k] = dp[i][j] + dp[j][k] + cost[i][j][k]
動態規劃將會定義兩個關鍵,一是狀態定義二是狀態裝
- 破壞成鏈
- 經典樹形dp
- 樹形背包
- 樹形背包優化
9. 排序
9.1 快速排序(三路版)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 三路快速排序(遞歸版本)
void quickSort3Way(vector<int>& nums, int left, int right) {if (left>=right) return; // 遞歸終止條件// 選擇基準值(選擇中間元素)int pivot = nums[left+(right-left)/2];// 初始化三個指針}
10. 并查集
- 基礎概念:并查集是一種樹型數據結構用于處理不相交集合(disjoint sets)的合并及查詢問題,常在使用中部用森林表示。
A?BA-BA?B - 合并方式:




—享元模式)
)






)



)


