遞歸

什么是遞歸

通俗來講，也就是函數自己調用自己的情況。像二叉樹的遍歷、快排算法、歸并算法等。

為什么會用到遞歸

本質：解決主問題的時候會衍生出相同的子問題，解決子問題的時候又衍生出相同的子問題。

主問題 -> 相同的子問題
子問題 -> 相同的子問題

一直往復…

如何理解遞歸

第一層次去理解：畫遞歸展開的細節圖
第二層次去理解：編寫和理解二叉樹中的題目
第三層次去理解：宏觀的看待遞歸的過程

我們要在第三層去理解：

1. 不要在意遞歸的細節展開圖
2. 把遞歸的函數當成一個黑盒（過程是怎么樣的不用管，看不到內部過程）
3. 相信這個黑盒一定能夠完成這個任務

如何寫好一個遞歸

1. 先找到相同的子問題！！！！！-> 決定了函數頭的設計
2. 只關心某一個子問題是如何解決的 -> 函數體的書寫
3. 注意一下遞歸函數的出口即可

把數據結構中二叉樹的題目，試著用第三層的方式去理解一下。

搜索 vs 深度優先遍歷 vs 深度優先搜索 vs 寬度（廣度）優先遍歷 vs 寬度（廣度）優先搜索 vs 暴搜

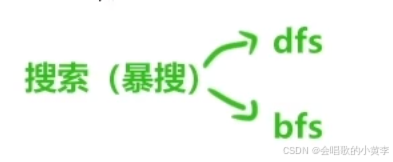
搜索其實就是把整個解空間遍歷一遍，本質就是暴力枚舉一遍所有的情況。也就是暴搜。

深度優先遍歷 vs 深度優先搜索（dfs）

通俗理解：一條道走到黑，走到不能再走時返回，遇到分支，和前面一樣的操作。

遍歷是形式，搜索是目的。所以他們兩可以理解為一個東西。

寬度（廣度）優先遍歷 vs 寬度（廣度）優先搜索（bfs）

通俗理解：一層一層剝開，也就是一層一層的去遍歷。

遍歷是形式，搜索是目的。所以他們兩可以理解為一個東西。

關系圖

拓展搜索問題

全排列問題：就是高中數學學的排列組合的問題，比如1，2，3，有哪幾種排列方式。如果數少還能列的出來，但是數一多就很容易一漏掉一些情況。

樹狀圖 (決策樹)

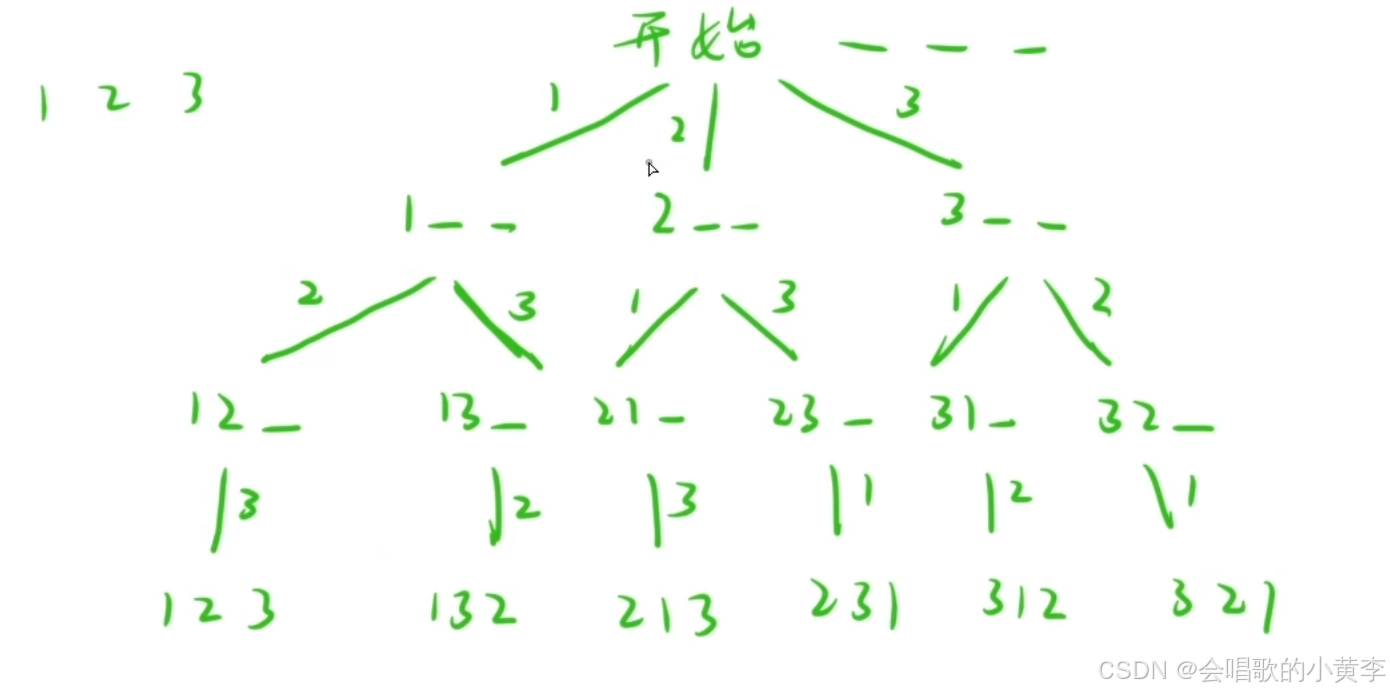
注意：不要局限于認為只有二叉樹和圖這些問題才能使用dfs和bfs，只要整個問題能用決策樹的方式畫出來的話，就能使用。

回溯和剪枝

回溯其實就是深搜里的一個小分支。

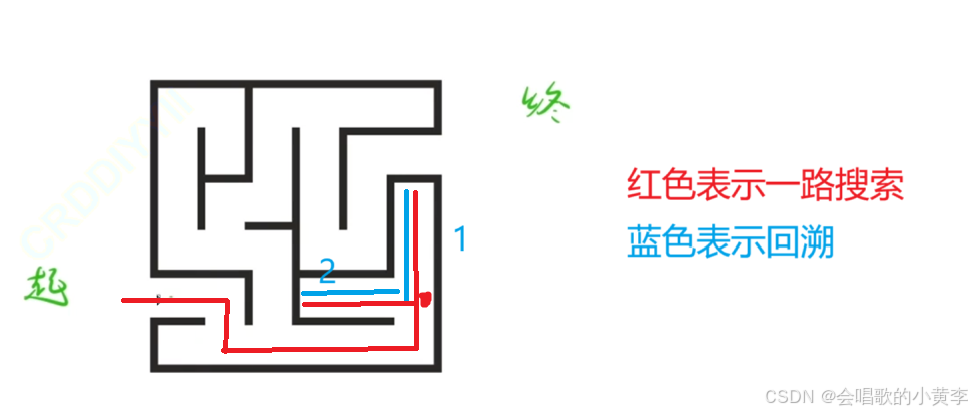
簡單理解一下回溯，就是嘗試某種情況的時候，發現走不通，返回到上一級的這個操作。也就是圖中紅色按1走的然后返回到紅點的過程。
再簡單理解一下剪枝，就是按1返回到紅點后再走到按2走，發現行不通再返回到紅點，此時往上往下都有路線，但是往上走已經嘗試過了，不用再走了。其實就是在分叉路口有兩種選擇的時候，但是我們已經明確知道了其中一個選擇不是我們最終想要的結果的時候，我們就把這個結果給略過。