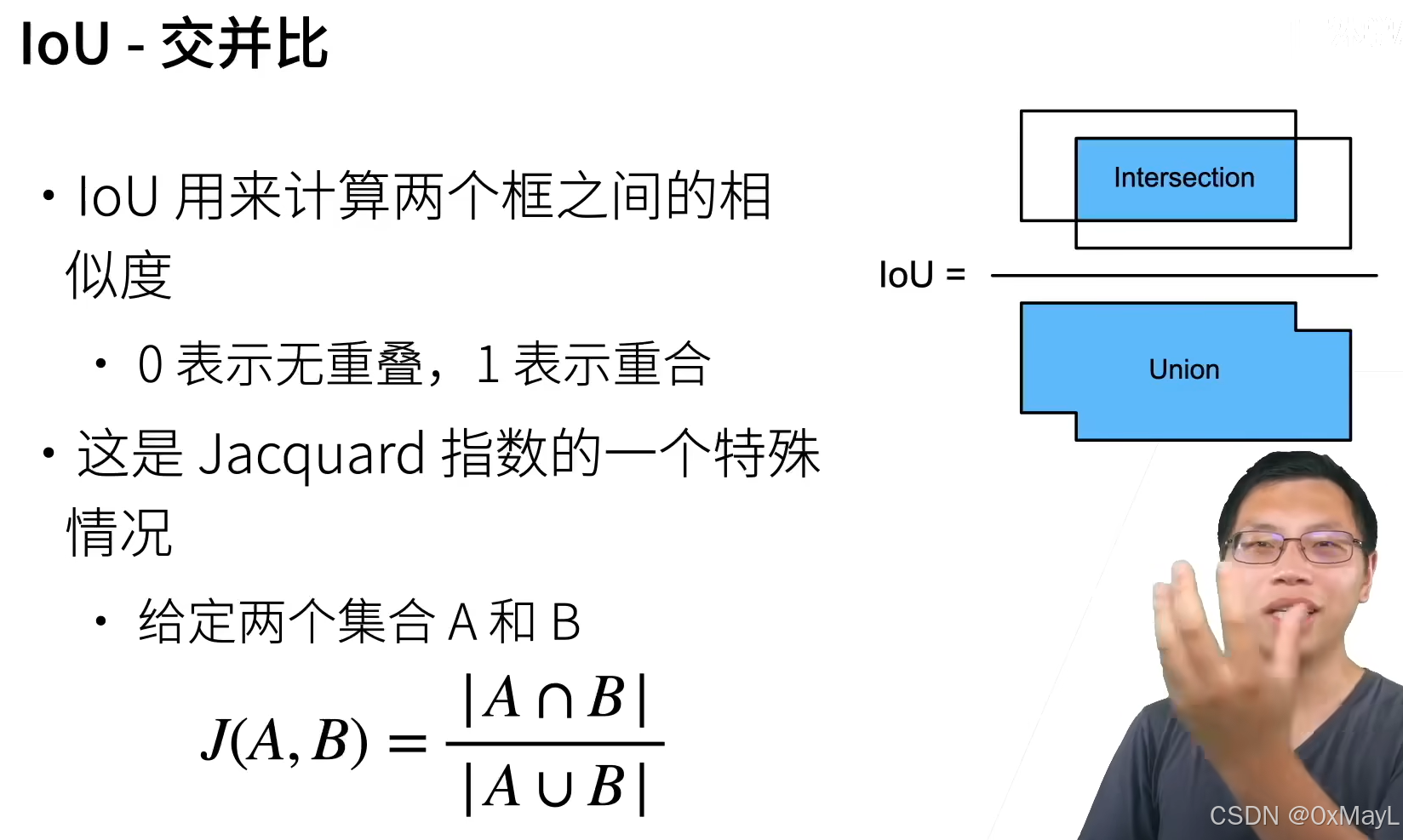
邊緣框

• 不是標準的x，y坐標軸。
• 邊緣框三種表示：左上右下下坐標，左上坐標+長寬，中心坐標+長寬
  

COCO

• 目標檢測數據集的格式：注意一個圖片有多個物體，使用csv或者文件夾結構的格式不可取。

錨框算法

• 生成很多個錨框
• 錨框之間和真實邊緣框匹配(標簽)。

• 一般的目標檢測模型不直接預測錨框的四個位置，而是預測與真實值的偏移。

• 對于背景類，會有個掩碼將偏移值設置為0.

• 匹配標簽后使用NMS輸出最后預測的錨框

在訓練數據中標注錨框

label:subsec_labeling-anchor-boxes

在訓練集中，我們將每個錨框視為一個訓練樣本。
為了訓練目標檢測模型，我們需要每個錨框的類別（class）和偏移量（offset）標簽，其中前者是與錨框相關的對象的類別，后者是真實邊界框相對于錨框的偏移量。
在預測時，我們為每個圖像生成多個錨框，預測所有錨框的類別和偏移量，根據預測的偏移量調整它們的位置以獲得預測的邊界框，最后只輸出符合特定條件的預測邊界框。

目標檢測訓練集帶有真實邊界框的位置及其包圍物體類別的標簽。
要標記任何生成的錨框，我們可以參考分配到的最接近此錨框的真實邊界框的位置和類別標簽。
下文將介紹一個算法，它能夠把最接近的真實邊界框分配給錨框。

將真實邊界框分配給錨框

給定圖像，假設錨框是$A_1,A_2,\dots ,A_{n_a}$，真實邊界框是$B_1,B_2,\dots ,B_{n_b}$，其中$n_a\ge n_b$。
讓我們定義一個矩陣$\mathbf{X}\in {\mathbb{R}}^{n_a\times n_b}$，其中第$i$行、第$j$列的元素$x_{ij}$是錨框$A_i$和真實邊界框$B_j$的IoU。
該算法包含以下步驟。

1. 在矩陣$\mathbf{X}$中找到最大的元素，并將它的行索引和列索引分別表示為$i_1$和$j_1$。然后將真實邊界框$B_{j_1}$分配給錨框$A_{i_1}$。這很直觀，因為$A_{i_1}$和$B_{j_1}$是所有錨框和真實邊界框配對中最相近的。在第一個分配完成后，丟棄矩陣中${i_1}^{\mathrm{th}}$行和${j_1}^{\mathrm{th}}$列中的所有元素。
2. 在矩陣$\mathbf{X}$中找到剩余元素中最大的元素，并將它的行索引和列索引分別表示為$i_2$和$j_2$。我們將真實邊界框$B_{j_2}$分配給錨框$A_{i_2}$，并丟棄矩陣中${i_2}^{\mathrm{th}}$行和${j_2}^{\mathrm{th}}$列中的所有元素。
3. 此時，矩陣$\mathbf{X}$中兩行和兩列中的元素已被丟棄。我們繼續，直到丟棄掉矩陣$\mathbf{X}$中$n_b$列中的所有元素。此時已經為這$n_b$個錨框各自分配了一個真實邊界框。
4. 只遍歷剩下的$n_a?n_b$個錨框。例如，給定任何錨框$A_i$，在矩陣$\mathbf{X}$的第$i^{\mathrm{th}}$行中找到與$A_i$的IoU最大的真實邊界框$B_j$，只有當此IoU大于預定義的閾值時，才將$B_j$分配給$A_i$。

下面用一個具體的例子來說明上述算法。
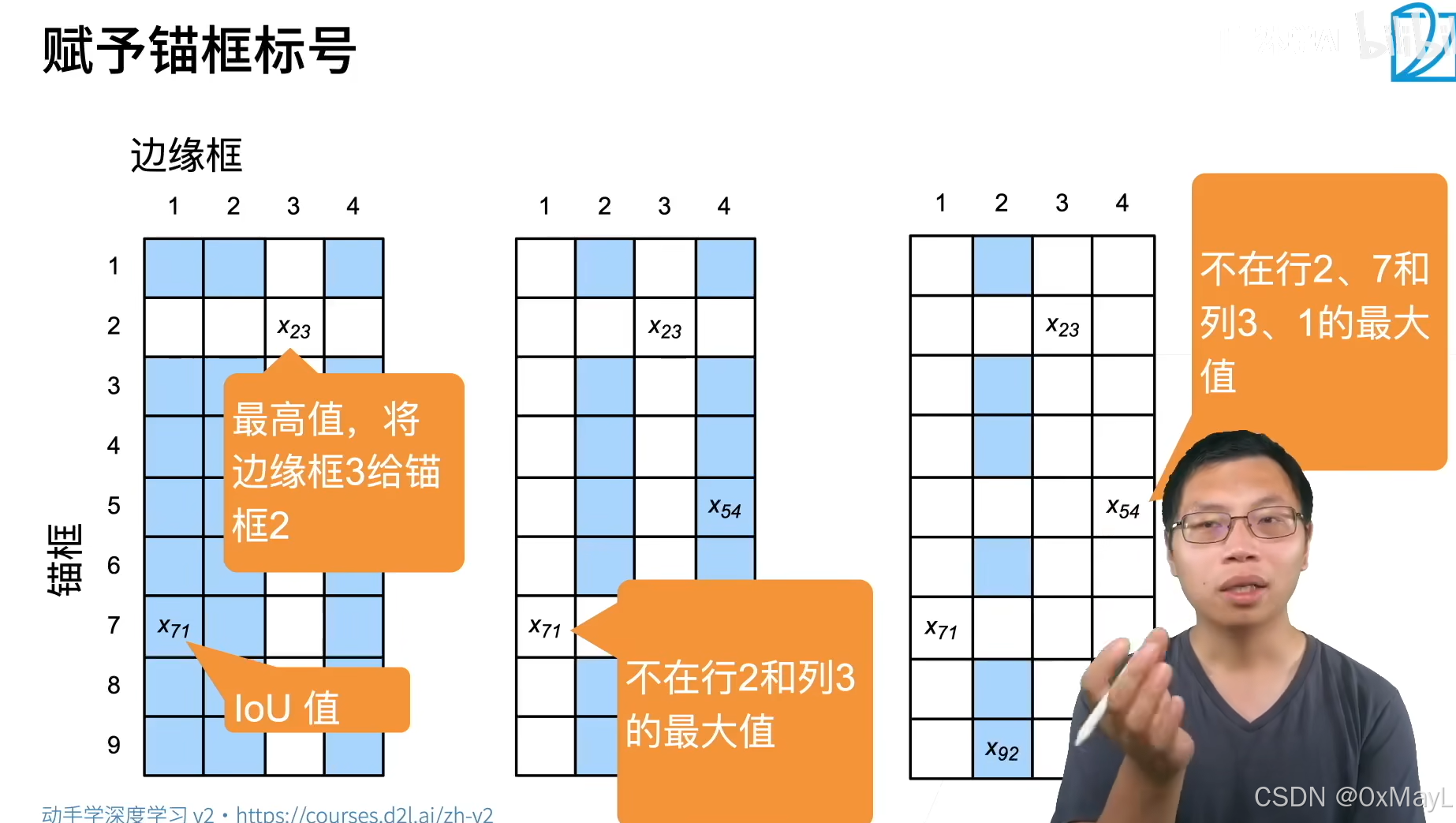
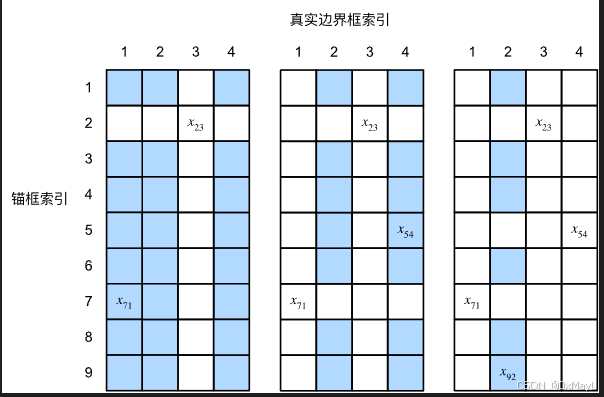
如 :numref:fig_anchor_label（左）所示，假設矩陣$\mathbf{X}$中的最大值為$x_{23}$，我們將真實邊界框$B_3$分配給錨框$A_2$。
然后，我們丟棄矩陣第2行和第3列中的所有元素，在剩余元素（陰影區域）中找到最大的$x_{71}$，然后將真實邊界框$B_1$分配給錨框$A_7$。
接下來，如 :numref:fig_anchor_label（中）所示，丟棄矩陣第7行和第1列中的所有元素，在剩余元素（陰影區域）中找到最大的$x_{54}$，然后將真實邊界框$B_4$分配給錨框$A_5$。
最后，如 :numref:fig_anchor_label（右）所示，丟棄矩陣第5行和第4列中的所有元素，在剩余元素（陰影區域）中找到最大的$x_{92}$，然后將真實邊界框$B_2$分配給錨框$A_9$。
之后，我們只需要遍歷剩余的錨框$A_1,A_3,A_4,A_6,A_8$，然后根據閾值確定是否為它們分配真實邊界框。

🏷fig_anchor_label

此算法在下面的assign_anchor_to_bbox函數中實現。

標記類別和偏移量

現在我們可以為每個錨框標記類別和偏移量了。
假設一個錨框$A$被分配了一個真實邊界框$B$。
一方面，錨框$A$的類別將被標記為與$B$相同。
另一方面，錨框$A$的偏移量將根據$B$和$A$中心坐標的相對位置以及這兩個框的相對大小進行標記。
鑒于數據集內不同的框的位置和大小不同，我們可以對那些相對位置和大小應用變換，使其獲得分布更均勻且易于擬合的偏移量。
這里介紹一種常見的變換。
[**給定框$A$和$B$，中心坐標分別為$(x_a,y_a)$和$(x_b,y_b)$，寬度分別為$w_a$和$w_b$，高度分別為$h_a$和$h_b$，可以將$A$的偏移量標記為：

$$\left(\frac{\frac{x_b?x_a}{w_a}?{\mu }_x}{{\sigma }_x},\frac{\frac{y_b?y_a}{h_a}?{\mu }_y}{{\sigma }_y},\frac{\log \frac{w_b}{w_a}?{\mu }_w}{{\sigma }_w},\frac{\log \frac{h_b}{h_a}?{\mu }_h}{{\sigma }_h}\right),$$
**]
其中常量的默認值為 ${\mu }_x={\mu }_y={\mu }_w={\mu }_h=0,{\sigma }_x={\sigma }_y=0.1$ ， ${\sigma }_w={\sigma }_h=0.2$。里插入圖片描述](https://i-blog.csdnimg.cn/direct/d0940b8fa45e4bf982f7ed9a5f981c99.png)

這種轉換在下面的 offset_boxes 函數中實現。

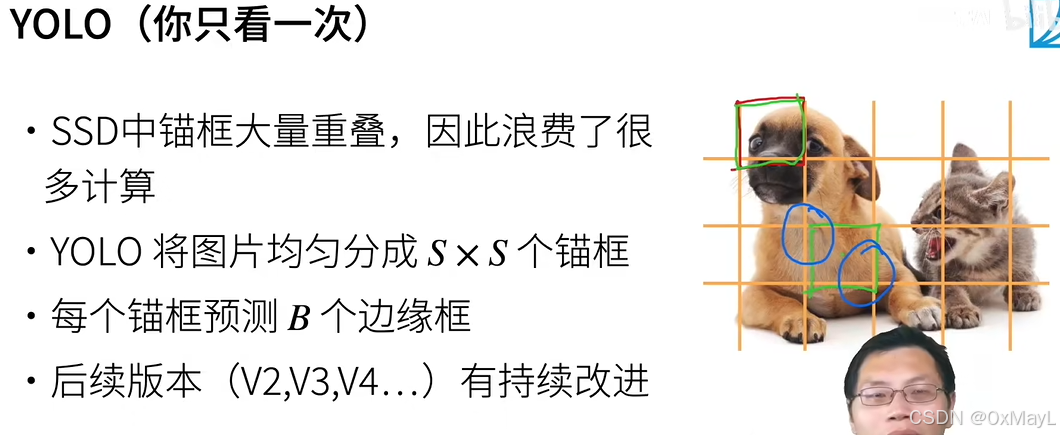
基于錨框的經典算法

語義分割

• 每個像素都會有一個label,這個label也是一個RGB顏色，三個通道

VOC數據集

• 圖片在JPEGImages，標簽在SegmentationClass中。
• 格式都為圖片
  

圖像增強的注意事項

在之前的實驗，例如 :numref:sec_alexnet— :numref:sec_googlenet中，我們通過再縮放圖像使其符合模型的輸入形狀。
然而在語義分割中，這樣做需要將預測的像素類別重新映射回原始尺寸的輸入圖像。
這樣的映射可能不夠精確，尤其在不同語義的分割區域。
為了避免這個問題，我們將圖像裁剪為固定尺寸，而不是再縮放。
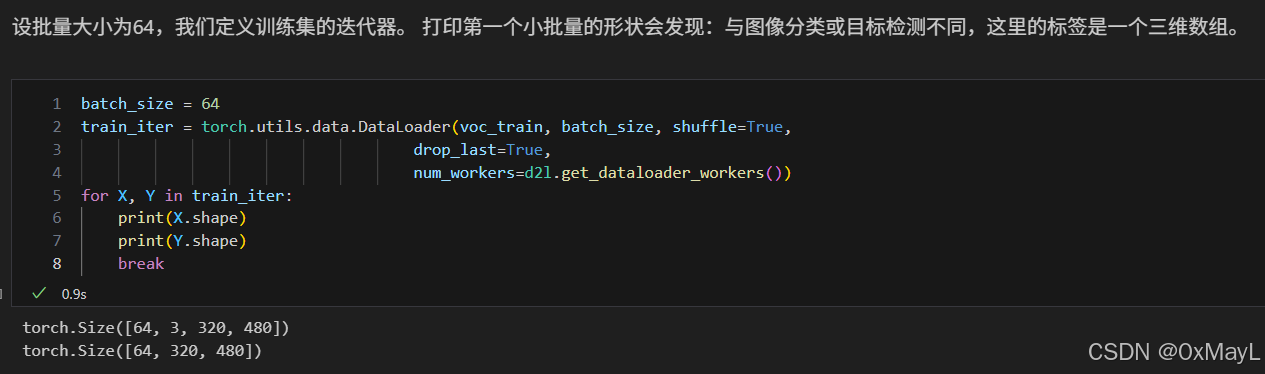
具體來說，我們[使用圖像增廣中的隨機裁剪，裁剪輸入圖像和標簽的相同區域]。
小細節：原標簽是一個3d RGB圖片，要進一步轉換為標簽才行。

    def __getitem__(self, idx):feature, label = voc_rand_crop(self.features[idx], self.labels[idx],*self.crop_size)return (feature, voc_label_indices(label, self.colormap2label))# 原標簽是一張RGB圖片,區分不同的背景，將其轉換為可學習的標簽。

將標簽圖片的RGB(3D)轉換為標簽索引(1D)

可見最后的dataloader標簽是一個圖片，每個像素是一個標簽。

正常卷積Conv2d

輸入和輸出通道，
kernel_size=2padding+1，且stride=1時，大小不變。
kernel_size=2padding，且stride=1時，大小不變。

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=1)
X.shape,conv(X).shape
(torch.Size([1, 10, 16, 16]), torch.Size([1, 20, 16, 16]))

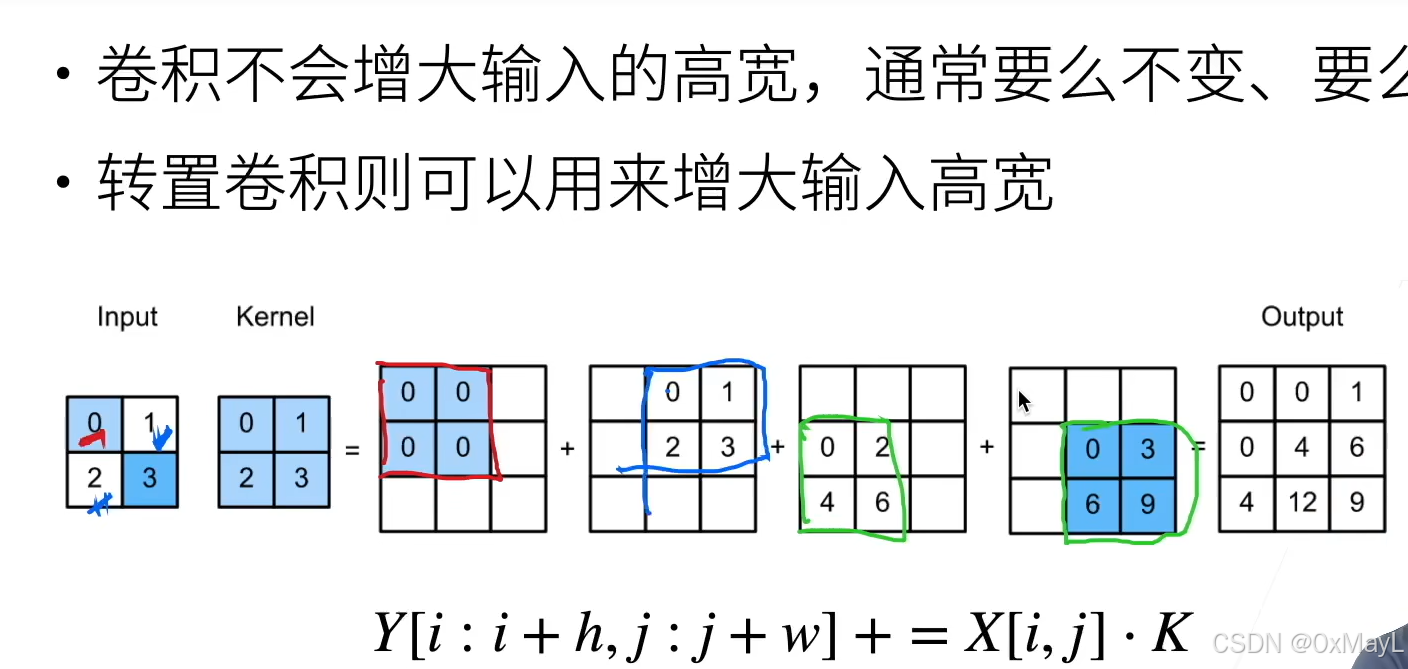
轉置卷積TransConv2d

利用卷積核的感受野，逆還原卷積。


輸入和輸出通道，
kernel_size=2padding+1，且stride=1時，大小不變。
kernel_size=2padding，且stride=1時，大小不變。
padding相當于直接減少輸出的大小，與conv相反，步長變為縮放k倍。

X = torch.rand(size=(1, 10, 16, 16))
tconv = nn.ConvTranspose2d(10, 20, kernel_size=5, padding=2, stride=1)
X.shape,tconv(X).shape
(torch.Size([1, 10, 16, 16]), torch.Size([1, 20, 16, 16]))

卷積和轉置卷積是可逆的

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

FCN

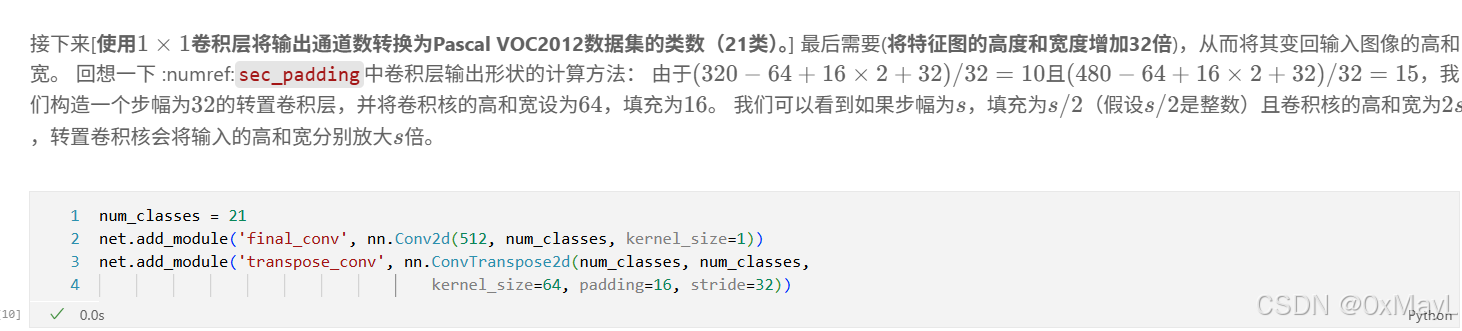
CNN+1x1卷積(降低通道數)+轉置卷積(重新縮放)

輸出是(通道數，寬，高)，其中通道數是用作類似全連接的標簽，與標簽數一致

pretrained_net = torchvision.models.resnet18(pretrained=True)
num_classes = 21
net.add_module('final_conv', nn.Conv2d(512, num_classes, kernel_size=1))
net.add_module('transpose_conv', nn.ConvTranspose2d(num_classes, num_classes,kernel_size=64, padding=16, stride=32))
RESNET輸出:
torch.Size([1, 512, 10, 15])
加入轉置卷積后輸入和輸出
torch.Size([1, 3, 320, 480])
torch.Size([1, 21, 320, 480])

參考文獻

動手學深度學習主頁