---

1.摘要

對現有建筑進行高質量的三維重建對于其維護、修復和管理至關重要。圖像采集中的有效視角規劃會顯著影響基于攝影測量的三維重建質量。復雜的建筑結構常常導致傳統視角規劃方法下的區域采樣不足，而過多的視角又會顯著增加計算資源和數據采集的負擔。為了解決這些問題，本文提出了一種新的先探索、后開發的視角規劃策略，以在盡可能少的視角下實現高質量的建筑重建。在探索階段，通過對圖像和粗模型的語義與幾何分析，識別出無人機禁飛區域與建筑關注區域。隨后結合建筑關注區域和重建相關因素（包括距離、入射角、視差角和圖像重疊度），構建了一個優化適應度函數。本文提出了一種改進麻雀搜索算法（MSSA），在優化機制上進行了增強，并融合了視角規劃的物理模型，從而能夠有效生成最優的視角集合。在開發階段設計了無碰撞的最短飛行路徑，使無人機能夠采集圖像并完成高質量的三維模型重建。

2.麻雀搜索算法SSA原理

【智能算法】麻雀搜索算法（SSA）原理及實現

3.整體框架

本文提出了一種優化的探索—開發無人機視角規劃策略，用來實現高質量的建筑三維重建。整個過程首先通過初步的環繞飛行采集圖像并構建粗略模型，在此基礎上，通過語義分析與幾何建模識別出建筑的關鍵關注區域與無人機禁飛區域，進而指導后續的精細規劃。在視角優化方面，本文構建了一個融合多種重建影響因素（包括距離、入射角、視差角和圖像重疊度）以及建筑關注區域的適應度函數，并引入了改進麻雀搜索算法（MSSA），用在連續可飛行空間中直接優化無人機視角的位置與朝向。此外，研究還設計了一種無碰撞的最短路徑規劃方法，確保無人機在執行任務時能夠高效、安全地穿越各個視角點。最后，通過執行優化后的第二次飛行，完成圖像采集并生成高質量的三維重建模型。

4.改進SSA算法

改進SSA融合視角規劃的物理模型，增強對初始視角分布的均勻性與多樣性控制，將優化過程劃分為全局探索與局部開發兩個階段，并設置動態可調的更新機制與角色比例。此外引入大小步長結合的局部開發策略，并取消僅接受更優解的限制，從而提高算法跳出局部最優的能力。算法以多個視角集合為優化對象，每個集合包含若干視角點，每個視角由位置與目標方向兩個三維坐標構成。為實現初始視角的空間均勻分布，無人機可飛行區域被劃分為多個子區域，每個區域內隨機生成等量的視角點，同時其目標方向則在建筑物的三維包圍盒中隨機設定。

改進SSA中生產者承擔全局搜索，通過對每個視角的位置與目標方向進行擾動，生產者能夠在搜索空間內廣泛探索，提升解的多樣性與覆蓋性。在優化初始階段，設置了較多的生產者$P{N}_1$，相比于后期的數量$P{N}_2$顯著增加，從而確保算法在早期具備更強的全局探索能力：
$$X_{i,j,k}^{t+1}=\{\begin{array}{ll}{X}_{i,j,k}^t+\alpha ?Q,ST>R_2& \\ X_{i,j,k}^t+Q,ST\le R_2& \end{array}$$

覓食者主要承擔局部開發任務，圍繞當前最優視角集合進行小步長的精細搜索：
X i , j , k t + 1 = X b e s t t + 1 d ∑ k = 1 d ∣ X i , j , k t ? X b e s t t ∣ ? r a n d ( { ? 1 , 1 } ) X_{i,j,k}^{t+1}=X_{best}^t+\frac{1}{d}\sum_{k=1}^d\left|X_{i,j,k}^t-X_{best}^t\right|\bullet rand(\{-1,1\}) Xi,j,kt+1?=Xbestt?+d1?k=1∑d? ?Xi,j,kt??Xbestt? ??rand({?1,1})

探索者在早期生成新的視點集來探索解空間，并在后期圍繞最佳視點集進行大步局部開發:
$$X_{i,j,k}^{t+1}=\{\begin{array}{c}init(),t<{\mathrm{T}}_{\max }/2\\ X_{best}^t+\beta ?\left|X_{i,j,k}^t?X_{best}^t\right|,t\ge {\mathrm{T}}_{\max }/2\end{array}$$

偽代碼

5.結果展示

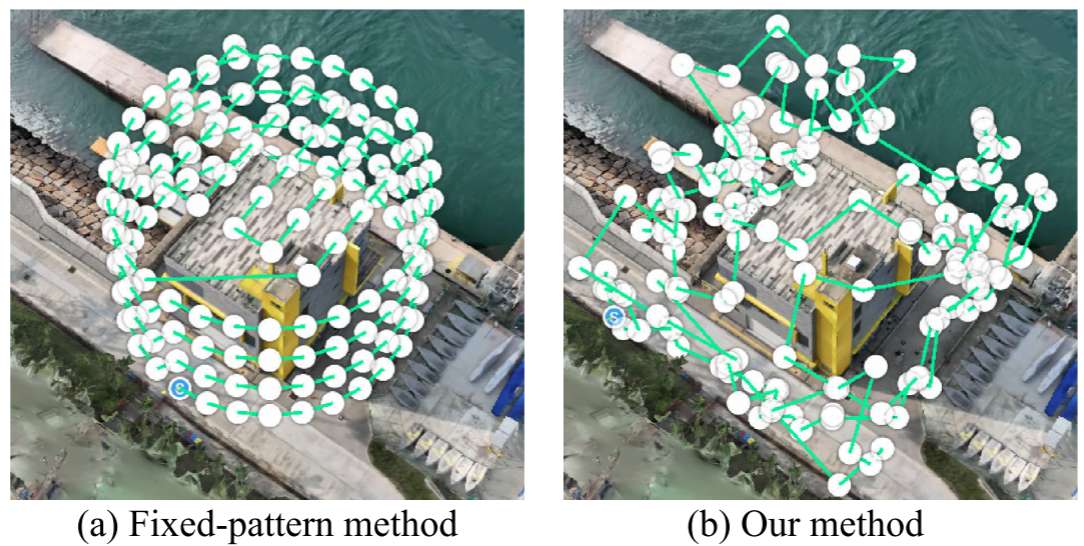
之前做的案例：

6.參考文獻

[1] Liang Z, Yang L, Liang Z, et al. Optimized UAV view planning for high-quality 3D reconstruction of buildings using a modified sparrow search algorithm[J]. Advanced Engineering Informatics, 2025, 65: 103344.

7.代碼獲取

8.讀者交流