一、梯度下降?

二、 線性方程怎么樣？

三、有噪音嗎？

?

四、讓我們看一個列子

?

五、如何優化

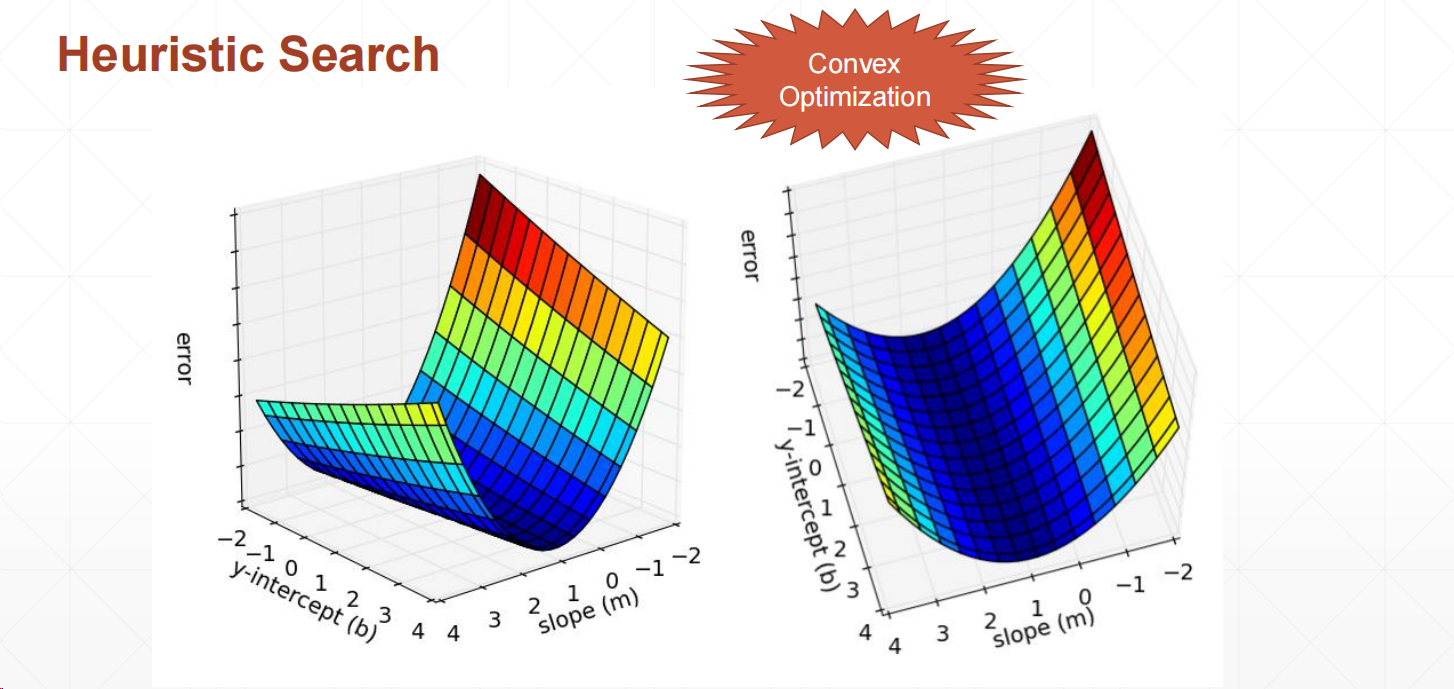
?啟發式搜索

學習進度?

?六、線性回歸、邏輯回歸、分類

?

總結、?

簡單線性回歸是一種統計方法，用于確定兩個變量之間的關系。具體來說，它試圖找到一條直線，能夠最好地描述因變量（通常稱為Y）和自變量（通常稱為X）之間的關系。這條直線可以通過公式 Y=β0+β1XY=β0?+β1?X 來表示，其中 β0β0? 是截距，β1β1? 是斜率。

線性回歸的目標是最小化實際值與預測值之間差的平方和，這種方法被稱為最小二乘法。通過這種方式，我們可以找到最能代表數據趨勢的直線。

代碼案例：

下面是使用Python和Scikit-Learn庫進行簡單線性回歸分析的例子。我們將創建一些虛擬數據來模擬一個簡單的線性關系，并使用這些數據訓練一個線性回歸模型。

# 導入必要的庫
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_splitprint("程序開始執行...")# 設置隨機種子以獲得可重復的結果
np.random.seed(0)# 創建虛擬數據
X = 2 * np.random.rand(100, 1)  # 自變量：廣告支出
y = 4 + 3 * X + np.random.randn(100, 1)  # 因變量：銷售額，基于一個線性方程加上一些噪聲print("數據生成完成！前5個樣本：")
print(X[:5])
print(y[:5])# 數據集劃分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)print("訓練/測試集分割完成！")# 創建線性回歸模型對象
lin_reg = LinearRegression()# 使用訓練數據擬合模型
lin_reg.fit(X_train, y_train)# 打印出截距和斜率
print(f'截距 (β0): {lin_reg.intercept_}')
print(f'斜率 (β1): {lin_reg.coef_[0]}')# 使用模型進行預測
y_pred = lin_reg.predict(X_test)print("預測完成！前5個預測值：")
print(y_pred[:5])# 可視化結果并保存為文件
plt.figure(figsize=(10, 6))  # 設置圖表大小
plt.scatter(X_test, y_test, color='blue', label='真實值')  # 繪制實際值
plt.plot(X_test, y_pred, color='red', label='預測值')  # 繪制預測值
plt.title('廣告支出與銷售額的關系')
plt.xlabel('廣告支出')
plt.ylabel('銷售額')
plt.legend()# 保存圖像到文件
image_path = "regression_result.png"
plt.savefig(image_path)
print(f"圖像已保存為 {image_path}")# 不調用 plt.show() 以避免圖形界面相關的問題

?