#基礎Machine Learning 算法（上）

機器學習算法的分類

機器學習算法大致可以分為三類：

監督學習算法 (Supervised Algorithms）:在監督學習訓練過程中，可以由訓練數據集學到或建立一個模式（函數 / learning model），并依此模式推測新的實例。該算法要求特定的輸入/輸出，首先需要決定使用哪種數據作為范例。例如，文字識別應用中一個手寫的字符，或一行手寫文字。主要算法包括神經網絡、支持向量機、最近鄰居法、樸素貝葉斯法、決策樹等。
無監督學習算法 (Unsupervised Algorithms):這類算法沒有特定的目標輸出，算法將數據集分為不同的組。
強化學習算法 (Reinforcement Algorithms):強化學習普適性強，主要基于決策進行訓練，算法根據輸出結果（決策）的成功或錯誤來訓練自己，通過大量經驗訓練優化后的算法將能夠給出較好的預測。類似有機體在環境給予的獎勵或懲罰的刺激下，逐步形成對刺激的預期，產生能獲得最大利益的習慣性行為。在運籌學和控制論的語境下，強化學習被稱作“近似動態規劃”（approximate dynamic programming，ADP）。

特點	監督學習	無監督學習
數據特性	數據帶有標簽或期望輸出	數據無標簽
學習目標	學習輸入輸出映射關系，用于預測未知數據的輸出（如分類或回歸）	發現數據的內在結構和模式（如聚類、降維等）
學習過程	利用標記數據進行訓練，模型通過比較預測輸出和真實標簽來調整參數	無標記數據，模型直接分析數據特征，發現模式和結構
常見算法	分類算法：決策樹、支持向量機、樸素貝葉斯等；回歸算法：線性回歸、嶺回歸等	聚類算法：k - 均值、層次聚類等；降維算法：主成分分析（PCA）、線性判別分析（LDA）等
應用場景	分類任務：垃圾郵件識別、圖像分類等；回歸任務：房價預測、股票價格預測等	聚類任務：客戶細分、文檔聚類等；降維任務：數據可視化、特征工程等

監督學習算法

線性回歸算法（Linear Regression）：用于回歸任務，通過擬合一條直線或超平面來預測連續值。
支持向量機算法（Support Vector Machine, SVM）：用于分類任務，通過找到一個超平面來最大化不同類別之間的間隔。
最近鄰居/k-近鄰算法（K-Nearest Neighbors, KNN）：用于分類和回歸任務，通過查找訓練集中最近的鄰居來預測新樣本的標簽。
邏輯回歸算法（Logistic Regression）：用于分類任務，通過 logistic 函數將線性回歸的輸出映射到概率值。
決策樹算法（Decision Tree）：用于分類和回歸任務，通過構建樹形結構來進行決策。
隨機森林算法（Random Forest）：用于分類和回歸任務，是一種集成學習方法，通過構建多個決策樹并綜合它們的結果來進行預測。
樸素貝葉斯算法（Naive Bayes）：用于分類任務，基于貝葉斯定理，并假設特征之間相互獨立。

無監督學習算法

k-平均算法（K-Means）：用于聚類任務，將數據集劃分為 k 個簇，每個簇由其均值表示。
降維算法（Dimensional Reduction）：包括主成分分析（PCA）、t-SNE 等，用于減少數據的特征維度，常用于數據可視化和特征工程。

1. 線性回歸算法 Linear Regression

回歸分析（Regression Analysis）是統計學的數據分析方法，目的在于了解兩個或多個變量間是否相關、相關方向與強度，并建立數學模型以便觀察特定變量來預測其它變量的變化情況。

線性回歸算法（Linear Regression）的建模過程就是使用數據點來尋找最佳擬合線。公式，y = mx + c，其中 y 是因變量，x 是自變量，利用給定的數據集求 m 和 c 的值。
線性回歸又分為兩種類型，即 簡單線性回歸（simple linear regression)，只有 1 個自變量；*多變量回歸（multiple regression)，至少兩組以上自變量。

公式

線性回歸的公式通常表示為：
$\ y = m \cdot x + c \$
其中：

( y ) 是因變量（我們想要預測的值）。
( x ) 是自變量（用于預測 ( y ) 的值）。
( m ) 是斜率，表示 ( x ) 變化一個單位時 ( y ) 的變化量。
( c ) 是截距，表示當 ( x = 0 ) 時 ( y ) 的值。

在多變量線性回歸中，公式可以擴展為：
$\ y = m_1 \cdot x_1 + m_2 \cdot x_2 + \ldots + m_n \cdot x_n + c \$
其中
$\ x_1, x_2, \ldots, x_n \$
是多個自變量，
$\ m_1, m_2, \ldots, m_n \$
是對應的系數。

例子

假設有如下數據集，描述了房屋面積（平方米）與房價（萬元）之間的關系：

房屋面積（( x )）	房價（( y )）
50	60
70	80
90	100
110	120
130	140

我們想找到一條直線來描述房屋面積和房價之間的關系，以便預測新房屋的房價。

簡單線性回歸

在這個例子中，我們只有一個自變量（房屋面積），因此使用簡單線性回歸。

計算平均值：
- $\ \bar{x} = \frac{50 + 70 + 90 + 110 + 130}{5} = 90 \$
- $\\bar{y} = \frac{60 + 80 + 100 + 120 + 140}{5} = 100 \$
計算斜率（( m )）：
$\ m = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \$
代入數據：
$\ m = \frac{(50-90)(60-100) + (70-90)(80-100) + (90-90)(100-100) + (110-90)(120-100) + (130-90)(140-100)}{(50-90)^2 + (70-90)^2 + (90-90)^2 + (110-90)^2 + (130-90)^2} \$
計算分子和分母：
- 分子：
  $\ (-40)(-40) + (-20)(-20) + (0)(0) + (20)(20) + (40)(40) = 1600 + 400 + 0 + 400 + 1600 = 4000 \$
- 分母：
  $KaTeX parse error: Can't use function '\(' in math mode at position 2: \?(?-40)^2 + (-20)^…$
- 斜率：
  $\ m = \frac{4000}{4000} = 1 \$
計算截距（( c )）：
$\ c = \bar{y} - m \cdot \bar{x} = 100 - 1 \cdot 90 = 10 \$
回歸方程：
$\ y = 1 \cdot x + 10 \$

預測

現在，我們可以使用這個方程來預測新房屋的房價。例如，如果房屋面積是 100 平方米，預測的房價為：
$\ y = 1 \cdot 100 + 10 = 110 \text{ 萬元} \$

多變量線性回歸

如果數據集中包含多個自變量，例如房屋面積和房間數量，我們使用多變量線性回歸：

房屋面積（( x_1 )）	房間數量（( x_2 )）	房價（( y )）
50	2	60
70	3	80
90	4	100
110	5	120
130	6	140

建立模型：
$\ y = m_1 \cdot x_1 + m_2 \cdot x_2 + c \$
使用線性回歸算法（如梯度下降或最小二乘法）來求解 ( m_1 )、( m_2 ) 和 ( c )。
預測：使用求得的參數來預測新房屋的房價。

通過這個簡單的例子，可以看出線性回歸如何通過擬合數據點來建立預測模型。

2. 支持向量機算法(Support Vector Machine,SVM)

支持向量機（SVM）是一種用于分類任務的監督學習算法。它的基本思想是將數據點映射到高維空間中，并找到一個最優的超平面來分隔不同類別的數據點。這個超平面的選擇不僅要正確分類訓練數據，還要最大化與最近數據點（支持向量）之間的距離，以提高模型的泛化能力。需要注意的是，支持向量機需要對輸入數據進行完全標記，僅直接適用于二分類任務，應用將多類任務需要減少到幾個二元問題。

舉例說明

假設有如下數據集，描述了兩類不同類別的點，用 x 和 y 表示兩個特征：

表格

復制

x	y	類別
1	2	A
2	3	A
3	3	A
6	7	B
7	8	B
8	9	B

我們的目標是找到一個超平面來分隔類別 A 和類別 B。

線性可分情況

數據可視化：
- 將數據點繪制在二維平面上，類別 A 的點分布在左邊，類別 B 的點分布在右邊。
尋找最優超平面：
- SVM 會找到一個超平面，使得這個超平面與最近的類別 A 和類別 B 的點之間的距離最大化。
- 假設找到的最優超平面方程為：
  
  w1x+w2y+b=0
- 支持向量是那些離超平面最近的點，例如類別 A 中的點 (3, 3) 和類別 B 中的點 (6, 7)。
間隔計算：
- 計算支持向量到超平面的距離，并最大化這個距離。
分類決策：
- 對于新的數據點，根據其在超平面的哪一側來判斷其類別。

非線性可分情況

假設數據集如下，描述了兩類不同類別的點，但這些點在二維空間中無法用一條直線分隔：

表格

復制

x	y	類別
1	1	A
2	2	A
3	3	A
2	4	B
3	5	B
4	6	B

數據可視化：
- 將數據點繪制在二維平面上，類別 A 的點分布在左下角，類別 B 的點分布在右上角，但無法用一條直線分隔。
核技巧：
- 使用徑向基函數核（RBF）將數據映射到高維空間中，使其在高維空間中線性可分。
- RBF 核函數定義為：
  
  K(x,x′)=exp(?γ∥x?x′∥2)
  
  其中，γ 是核函數的參數，控制映射到高維空間的程度。
尋找最優超平面：
- 在高維空間中找到一個超平面來分隔數據點。
- 支持向量是那些離超平面最近的點。
分類決策：
- 對于新的數據點，將其映射到高維空間后，根據其在超平面的哪一側來判斷其類別。

3. 最近鄰居/k-近鄰算法 (K-Nearest Neighbors,KNN)

KNN算法是一種基于實例的學習，或者是局部近似和將所有計算推遲到分類之后的惰性學習。用最近的鄰居（k）來預測未知數據點。k 值是預測精度的一個關鍵因素，無論是分類還是回歸，衡量鄰居的權重都非常有用，較近鄰居的權重比較遠鄰居的權重大。

KNN 算法的缺點是對數據的局部結構非常敏感。計算量大，需要對數據進行規范化處理，使每個數據點都在相同的范圍。

KNN 也可以用于回歸問題。例如，我們有一組房屋，的數據包括房屋的面積、房齡等特征以及房價（目標變量）。當我們想要預測一套新房子的價格時，就找到訓練集中與新房子在面積和房齡等方面最相似的 k 個房子，然后取這 k 個房子價格的平均值作為新房子的預測價格。不過，回歸問題中的 KNN 實現細節和應用場景相對分類問題有所不同，主要在于輸出結果是從連續值中預測而不是分類標簽。

4. 邏輯回歸算法 Logistic Regression

邏輯回歸是一種用于解決二分類問題的監督學習算法（也可以通過一些擴展方法用于多分類）。它的目標是找到一個決策邊界，將不同類別的數據點分開。例如，在一個二維平面上，這可能是一條直線或曲線，用于區分兩類樣本。

邏輯回歸算法（Logistic Regression）一般用于需要明確輸出的場景，如某些事件的發生（預測是否會發生降雨）。通常，邏輯回歸使用某種函數將概率值壓縮到某一特定范圍。

邏輯回歸模型的輸出是一個概率值，表示樣本屬于某個類別的概率。這個概率值通過邏輯函數（也稱為 sigmoid 函數）來計算。邏輯函數的數學表達式為：

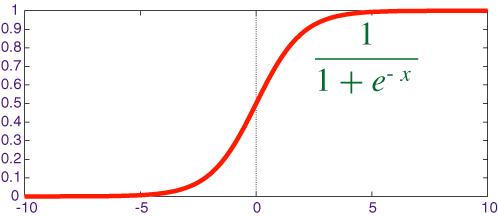
其中 z 是線性組合（如 z=θ0+θ1x1+θ2x2+?+θnx**n）。

在這里插入圖片描述

5.決策樹算法 Decision Tree

決策樹（Decision tree）是一種特殊的樹結構，由一個決策圖和可能的結果（例如成本和風險）組成，用來輔助決策。機器學習中，決策樹是一個預測模型，樹中每個節點表示某個對象，而每個分叉路徑則代表某個可能的屬性值，而每個葉節點則對應從根節點到該葉節點所經歷的路徑所表示的對象的值。決策樹僅有單一輸出，通常該算法用于解決分類問題。

一個決策樹包含三種類型的節點：

決策節點：通常用矩形框來表示
機會節點：通常用圓圈來表示
終結點：通常用三角形來表示

? 簡單決策樹算法案例，確定人群中誰喜歡使用信用卡。考慮人群的年齡和婚姻狀況，如果年齡在30歲或是已婚，人們更傾向于選擇信用卡，反之則更少。
通過確定合適的屬性來定義更多的類別，可以進一步擴展此決策樹。在這個例子中，如果一個人結婚了，他超過30歲，他們更有可能擁有信用卡（100% 偏好）。測試數據用于生成決策樹。

總結

算法名稱	基本原理	優點	缺點	適用場景
線性回歸	通過擬合一條直線或多維超平面來預測連續值。	簡單易懂，計算高效。	只能處理線性關系，對異常值敏感。	回歸任務，如房價預測。
支持向量機(SVM)	在高維空間中尋找一個最優超平面來分隔不同類別的數據點。	分類效果好，泛化能力強。	對參數選擇敏感，計算復雜度高。	分類任務，尤其是高維數據。
K-近鄰(KNN)	基于最近的鄰居來預測未知數據點的類別或值。	簡單易懂，適用于非線性數據。	計算量大，對數據局部結構敏感。	分類和回歸任務。
邏輯回歸	通過邏輯函數將線性回歸的輸出映射到概率值，用于二分類問題。	模型可解釋性強。	假設特征獨立，可能不適用于強相關特征數據。	二分類任務，如垃圾郵件識別。
決策樹	通過構建樹形結構來進行決策，每個節點表示某個屬性的測試。	模型可解釋性強，能處理非線性關系。	容易過擬合，對數據波動敏感。	分類任務，如客戶細分。