6.7.圖的深度優先遍歷(英文縮寫DFS)

樹是特殊的圖，沒有回路的圖就是樹
BFS與DFS的區別在于，BFS使用了隊列，DFS使用了棧

一.深度優先遍歷：

1.樹的深度優先遍歷：

樹的深度優先遍歷分為先根遍歷和后根遍歷。

以樹的先根遍歷為例：

上述圖片里樹的先根遍歷序列為1、2、5、6、3、4、7、8
樹的先根遍歷中新找到的相鄰結點一定是沒有被訪問過的

2.圖的深度優先遍歷：

visited數組用來記錄圖中的頂點是否被訪問過，MAX_VERTEX_NUM是圖中頂點的最大個數，DFS函數的形參Graph G和int v分別表示圖和圖的頂點編號，visit函數用于訪問頂點，visit(v)表示訪問第v號頂點，visited[v]=true表示第v號頂點被訪問過
DFS函數中的for循環，其中FirstNeighbor(G,v)用來找第v號頂點在G中的第一個鄰接點，若存在該鄰接點，返回該第一個鄰接點的編號，賦值給w，如果w非負，執行for循環，首先判斷是否執行if語句，若符合條件!visited[w]為true即第w號頂點沒有被訪問過，那么就執行if語句，調用DFS函數，該層for循環結束，再執行NextNeighbor(G,v,w)函數，第w號頂點是第v號頂點的第一個鄰接點，找除了第w號頂點外第v號頂點的的下一個鄰接點，找到了返回該鄰接點的頂點號，賦值給w，判斷是否非負，若非負，繼續執行for循環，如不是非負即小于0，跳出for循環
圖的深度優先遍歷類似樹的先根遍歷，都是先訪問完一個結點，然后再用一個循環依次檢查和這個結點相鄰的其他結點，然后進行更深一層的訪問，只不過對于圖的深度優先遍歷，增加了一個數組用來標記頂點是否被訪問過
對于圖而言，通過某一個頂點找到的與之相鄰的其他頂點有可能是已經被訪問過的，所以可以設置一個數組，用來標記每一個頂點是否被訪問過

3.模擬圖的深度優先遍歷的執行過程：

如下圖，以上述圖片的圖為例，假設從2號頂點出發深度優先遍歷該圖，所以第一次調用DFS函數的時候，傳入的v的值為2，然后調用visit函數訪問2號頂點，修改2號頂點對應的visited的值為true，表示2號頂點已經被訪問過，for循環用來檢查和2號頂點相鄰的其他頂點，和2號頂點相鄰的頂點是1、6號頂點，其中和2號頂點相鄰的第一個頂點是1號頂點，此時1號頂點沒有被訪問過：

如下圖，因此第二次調用DFS函數時傳入的參數為1，然后調用visit函數訪問1號頂點，修改1號頂點對應的visited的值為true，表示1號頂點已經被訪問過，for循環用來檢查和1號頂點相鄰的其他頂點，和1號頂點相鄰的頂點是2、5號頂點，其中和1號頂點相鄰的第一個頂點是2號頂點，由于2號頂點對應的visited的值為true即已經被訪問過，因此2號頂點會被跳過，通過for循環找到下一個和1號頂點相鄰接的頂點是5號頂點：

如下圖，因此第三次調用DFS函數時傳入的參數為5，然后調用visit函數訪問5號頂點，修改5號頂點對應的visited的值為true，表示5號頂點已經被訪問過，for循環用來檢查和5號頂點相鄰的其他頂點，和5號頂點相鄰的頂點是1號頂點，由于1號頂點對應的visited的值為true即已經被訪問過，因此1號頂點會被跳過，此時和5號頂點相鄰的所有頂點全部訪問完畢，意味著5號頂點對應的for循環什么都不會做：

如下圖，所以5號頂點對應的DFS函數執行完畢，之后就會返回上一層的遞歸調用，即1號頂點這一層：

如下圖，由于之前處理的5號頂點已經是1號頂點的最后一個鄰接點，所以1號頂點的for循環執行完畢，因此1號頂點對應的DFS函數執行結束，最終返回上一層的遞歸調用，即2號頂點這一層：

如下圖，此時2號頂點的第一個鄰接點即1號頂點已經被處理完，通過NextNeighor(G,v,w)函數找到除了1號頂點之外后一個和2號頂點相鄰接的頂點即6號頂點，6號頂點此時還沒有被訪問過：

如下圖，因此接下來調用DFS函數時傳入的參數為6，然后調用visit函數訪問6號頂點，修改6號頂點對應的visited的值為true，表示6號頂點已經被訪問過，for循環用來檢查和6號頂點相鄰的其他頂點，和6號頂點相鄰的頂點是2、3、7號頂點，由visited數組可知2號頂點已經被訪問過，因此會跳過2號頂點，開始訪問3號頂點：

如下圖，因此接下來調用DFS函數時傳入的參數為3，然后調用visit函數訪問3號頂點，修改3號頂點對應的visited的值為true，表示3號頂點已經被訪問過，for循環用來檢查和3號頂點相鄰的其他頂點，和3號頂點相鄰的頂點是4、6、7號頂點，第一個被訪問的頂點是4號頂點，由visited數組可知4號頂點還沒有被訪問過：

如下圖，因此接下來調用DFS函數時傳入的參數為4，然后調用visit函數訪問4號頂點，修改4號頂點對應的visited的值為true，表示4號頂點已經被訪問過，for循環用來檢查和4號頂點相鄰的其他頂點，和4號頂點相鄰的頂點是3、7、8號頂點，第一個被訪問的頂點是3號頂點，由visited數組可知3號頂點已經被訪問過，因此會跳過3號頂點，開始訪問7號頂點：

如下圖，因此接下來調用DFS函數時傳入的參數為7，然后調用visit函數訪問7號頂點，修改7號頂點對應的visited的值為true，表示7號頂點已經被訪問過，for循環用來檢查和7號頂點相鄰的其他頂點，和7號頂點相鄰的頂點是3、4、6、8號頂點，由visited數組可知，和7號頂點相鄰接的頂點中，只有8號頂點還沒有被訪問過，因此開始訪問8號頂點：

如下圖，因此接下來調用DFS函數時傳入的參數為8，然后調用visit函數訪問8號頂點，修改8號頂點對應的visited的值為true，表示8號頂點已經被訪問過，for循環用來檢查和8號頂點相鄰的其他頂點，和8號頂點相鄰的頂點是4、7號頂點，由visited數組可知，4、7號頂點都已經被訪問過，所以8號頂點的DFS函數執行完畢：

如下圖，返回上一層即7號頂點這一層，此時和7號頂點相鄰的所有頂點都已經全部被訪問完畢，所以繼續返回上一層：

如下圖，返回到4號頂點這一層，此時和4號頂點相鄰的所有頂點都已經全部被訪問完畢，所以繼續返回上一層：

如下圖，其他的類似，最終函數調用棧清空，上述圖片的圖遍歷完畢：

如上圖，最終得出從2號頂點出發，進行上述圖的深度優先遍歷，得到的深度遍歷序列為2，1，5，6，3，4，7，8。

4.圖的深度優先遍歷算法存在的問題與優化：

上述圖片的代碼存在一個問題，就是如果遍歷的圖是非連通圖，則無法遍歷完所有頂點，如下圖所示：

例如從2號頂點出發進行深度優先遍歷上述圖片里的圖，調用DFS函數，可以遍歷完1、2、3、4、5、6、7、8號頂點，但9、10、11號頂點無法遍歷到，解決方案如下：

DFSTraverse函數的形參Graph G表示圖；vexnum表示圖中頂點的個數，G.vexnum表示圖中頂點的個數，v是頂點編號
DFSTraverse函數的第一個for循環用來把visited數組全部賦值為false，表示圖中所有頂點都沒有被訪問過
DFSTraverse函數的第二個for循環用來檢查是否有頂點還沒有被訪問過，如果有，visited[v]的值為false，!visited[v]的值為true，就會執行if語句再次調用DFS函數把未訪完的頂點訪問完畢
注：DFSTraverse函數的第二個for循環必須從第一個頂點出發開始遍歷，如果從中間的頂點出發開始遍歷，就會使得前面的頂點無法遍歷到->如上圖，必須從1號頂點出發，由于是非連通圖，只能把1、2、3、4、5、6、7、8號頂點訪問完，此時發現第9號頂點對應visited的值為false，意味著9號頂點還沒有被訪問，因此從9號頂點出發，再次調用DFS函數訪問剩下的頂點，通過9號頂點就可以把9、10、11號頂點全部訪問完，最終上述圖片的圖深度優先遍歷完畢

二.圖的深度優先遍歷算法的空間復雜度：

如上圖，圖的深度優先遍歷算法的空間復雜度主要取決于DFS函數的遞歸調用。

1.最壞的情況：

如上圖，比如從1號頂點出發開始深度優先遍歷圖，那么DFS函數遞歸調用棧的深度就會與圖中的頂點個數相等（因為1號頂點與2、3、4、5、6、7、8號頂點都鄰接，意味著函數遞歸調用棧會把圖中8個頂點即所有頂點都入棧），假設圖中有V個頂點，因此最壞的情況為O( |V| )->之所以這個是最壞情況，是因為遞歸深度達到了最大值。

2.最好的情況：

如上圖，比如從1號頂點出發開始深度優先遍歷圖，顯然在這種情況下DFS函數遞歸調用棧最多只會有兩層（一層是當前訪問的頂點，一層是與該頂點相鄰接的頂點，不存在第二個與該頂點相鄰接的頂點），也就是說只需要常數級即O(1)的空間復雜度。（注：訪問頂點時函數遞歸調用棧最少會有一層，這一層是當前訪問的頂點，該頂點不存在鄰接點，頂點全部訪問完畢時或者不訪問頂點時函數遞歸調用棧為0層）

3.注意：做題時，題目問圖的深度優先遍歷算法的空間復雜度，沒有特別說明的情況下，要答O( |V| )即最壞的情況。

三.圖的深度優先遍歷算法的時間復雜度：

核心：無論是BFS還是DFS，計算時間復雜度都可以簡化為計算訪問各個頂點所需要的時間加探索各條邊/弧所需要的時間

1.如果圖采用鄰接矩陣存儲：

假設圖中有V個頂點，訪問|V|個頂點就需要O( |V| )的時間，因為需要遍歷，

探索和某一個頂點相鄰的邊只需要遍歷該頂點對應的一整行（或一整列，因為此時是無向圖，無向圖的鄰接矩陣是對稱的）的數據即可，所以查找每個頂點的鄰接點即鄰接的邊需要O( |V| )的時間，

由于總共有|V|個頂點，所以整體來看時間復雜度就是O( |V| * |V| )。

2.如果圖采用鄰接表存儲：

假設圖中有V個頂點，訪問|V|個頂點就需要O( |V| )的時間，因為需要遍歷，

假設圖中有E條邊，查找某個頂點的鄰接點即鄰接的邊共需要O( |E| )的時間，因為查找某個頂點的鄰接點即鄰接的邊只需要遍歷該頂點對應的鏈表即可，鏈表可能包含所有的邊，所以共需要O( |E| )的時間，

由于需要先查找所要操作的頂點，再找鄰接的邊，所以時間復雜度為O( |V|+|E| )。

四.深度優先遍歷序列：從哪一個頂點開始遍歷（入棧），遍歷結束時就是哪個頂點最后一個出棧（先進后出）

假設圖使用了鄰接矩陣或者鄰接表存儲，

如上圖，鄰接表中各個鏈表中頂點號都是從左向右遞增的，因此，對于某一個頂點，要找到與該頂點相鄰的其他頂點，在該鄰接表中找到的順序與左邊的鄰接矩陣找到的順序是一致的，因為鄰接矩陣的頂點號也是從左向右遞增的。

1.從2號頂點出發進行深度優先遍歷整個圖：

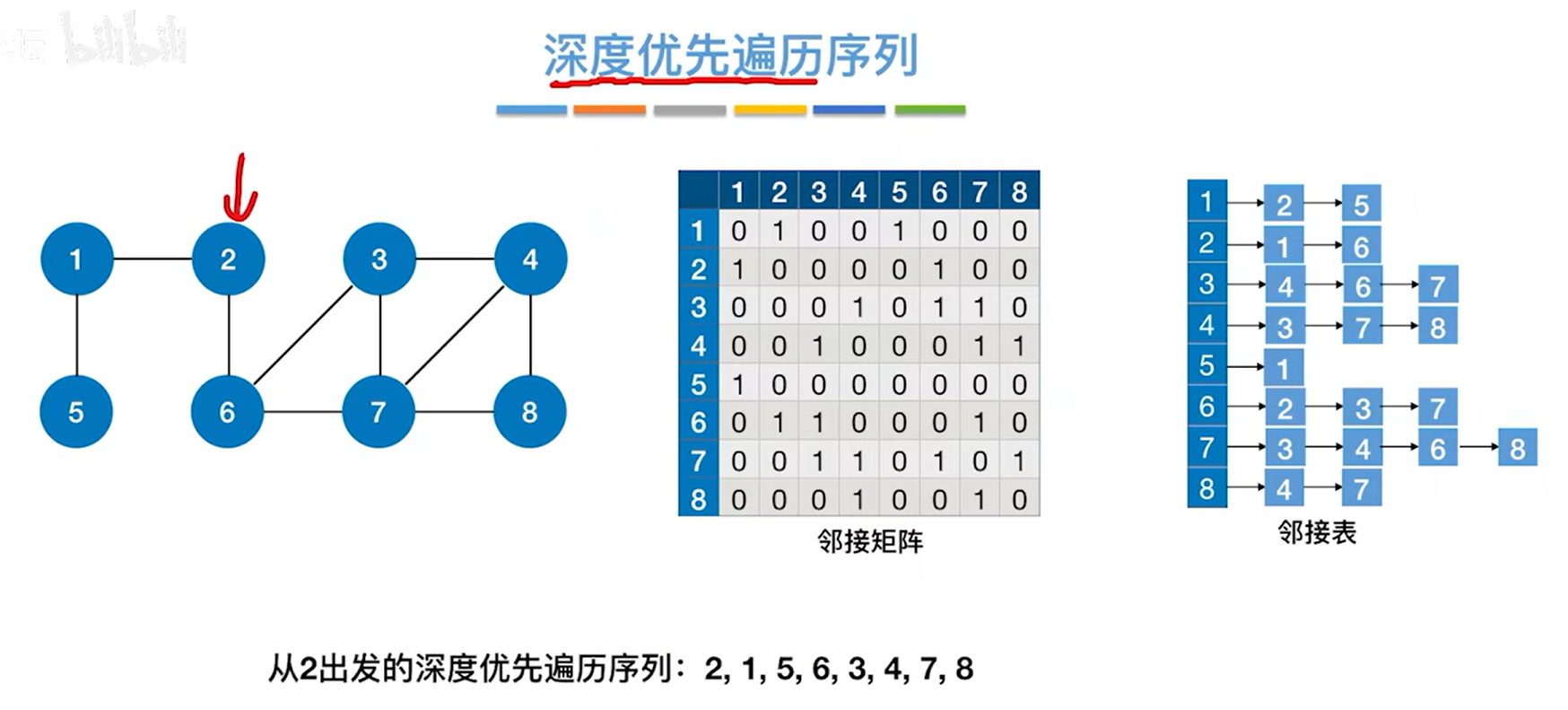
在鄰接矩陣和鄰接表這兩種情況下，如果從2號頂點出發進行深度優先遍歷整個圖，得到的遍歷序列都是2，1，5，6，3，4，7，8（因為此時鄰接矩陣和鄰接表存儲頂點的編號都是遞增的）。

2.從3號頂點出發進行深度優先遍歷整個圖：（詳細遍歷過程）

如下圖，假設圖使用鄰接表存儲：

如上圖，第一個訪問3號頂點，和3號頂點相鄰的第一個頂點是4號頂點（這個直接看3號頂點對應的鏈表即可知道3號頂點與哪些頂點鄰接，其他同理），因此

如上圖，第二個訪問4號頂點，根據DFS的規則，此時要從4號頂點出發找其他和4號頂點相鄰且沒有被訪問的頂點，與4號頂點相鄰的第一個頂點即3號頂點已經被訪問過了，因此跳過3號頂點，與4號頂點相鄰的第二個頂點即7號頂點沒有被訪問過，因此

如上圖，第三個訪問7號頂點，與7號頂點相鄰的第一個頂點即3號頂點已經被訪問過了，因此跳過3號頂點，與7號頂點相鄰的第二個頂點即4號頂點也已經被訪問過了，因此跳過4號頂點，與7號頂點相鄰的第三個頂點即6號頂點沒有被訪問過，因此

如上圖，第四個訪問6號頂點，與6號頂點相鄰的第一個頂點即2號頂點沒有被訪問過，因此

如上圖，第五個訪問2號頂點，與2號頂點相鄰的第一個頂點即1號頂點沒有被訪問過，因此

如上圖，第六個訪問1號頂點，與1號頂點相鄰的第一個頂點即2號頂點已經被訪問過了，因此跳過2號頂點，與1號頂點相鄰的第二個頂點即5號頂點沒有被訪問過，因此

如上圖，第七個訪問5號頂點，與5號頂點相鄰的第一個頂點即1號頂點已經被訪問過了，因此跳過1號頂點->此時5號頂點對應的這一層DFS結束，退回到上一層即1號頂點對應的這一層DFS：

如上圖，此時與1號頂點相鄰的2、5號頂點全部被訪問過，因此1號頂點對應的這一層DFS結束，退回到上一層即2號頂點對應的這一層DFS：

如上圖，2號頂點對應的這一層DFS還有6號頂點沒有檢查過，但6號頂點已經訪問過了，所以退回到上一層即6號頂點對應的這一層DFS：

如上圖，和6號頂點相鄰的頂點中還剩3、7號頂點沒有檢查，但3、7號頂點已經被訪問過了，因此退回到上一層即7號頂點對應的這一層DFS：

如上圖，和7號頂點相鄰的頂點中還剩下8號頂點沒有被訪問過：

如下圖，所以第八個訪問8號頂點，

如上圖，與8號頂點相鄰的頂點中4、7號頂點全部被訪問過，所以退回到上一層即7號頂點對應的這一層DFS，

此時7號頂點對應的這一層DFS結束，退回到上一層即4號頂點對應的這一層DFS，

和4號頂點相鄰的頂點中還剩8號頂點沒有檢查，但8號頂點已經被訪問過了，因此退回到上一層即3號頂點對應的這一層DFS，

此時還剩下6、7號頂點沒有檢查，但6、7號頂點已經被訪問了，因此退出3號頂點對應的這一層DFS，

最終該圖的深度優先遍歷結束，得到的遍歷序列為3、4、7、6、2、1、5、8：

3.從1號頂點出發進行深度優先遍歷整個圖：

4.細節：當圖使用鄰接表存儲的話，由于鄰接表的表現方式不唯一即頂點對應的鏈表中頂點號順序不固定，因此如果從某一個頂點出發深度優先遍歷得到的圖的序列也可能不一樣

對于圖而言，它的鄰接矩陣存儲的表示方式是唯一的，但鄰接表的表示方式不唯一，

所以如果圖使用鄰接表存儲的話，從某一頂點出發深度優先遍歷圖，最終得到的遍歷序列也可能不同，這個與BFS一樣。

如上圖，圖使用上述圖片呈現的鄰接表存儲，從2號頂點出發，得到的深度優先遍歷序列為2、1、5、6、3、4、7、8，

如下圖，此時把鄰接表的內容稍作修改即把頂點對應的鏈表中的頂點號換一下順序：

從2號頂點出發開始深度優先遍歷圖，

第一個訪問2號頂點，與2號頂點相鄰的第一個頂點即6號頂點沒有被訪問過（這個直接看頂點對應的鏈表即可）

第二個訪問6號頂點，與6號頂點相鄰的第一個頂點即2號頂點已經被訪問過，因此跳過2號頂點，與6號頂點相鄰的第二個頂點即7號頂點還沒有被訪問過，

第三個訪問7號頂點，與7號頂點相鄰的第一個頂點即6號頂點已經被訪問過，因此跳過6號頂點，與7號頂點相鄰的第二個頂點即8號頂點還沒有被訪問過，

第四個訪問8號頂點，與8號頂點相鄰的第一個頂點即4號頂點還沒有被訪問過，

第五個訪問4號頂點，與4號頂點相鄰的第一個頂點即3號頂點還沒有被訪問過，

第六個訪問3號頂點，與3號頂點相鄰的頂點有6、7、4號頂點，這些頂點都被訪問過，

因此3號頂點對應的DFS遞歸調用結束，

返回到4號頂點對應的DFS，與4號頂點相鄰的只剩下8、7號頂點沒有檢查過，但8、7號頂點都被訪問過，

所以繼續返回到8號頂點對應的DFS，與8號頂點相鄰的7號頂點也已經被訪問過，

所以繼續返回到7號頂點對應的DFS，與7號頂點相鄰的3、4號頂點也已經被訪問過，

所以繼續返回到6號頂點對應的DFS，與6號頂點相鄰的3號頂點也已經被訪問過，

所以繼續返回到2號頂點對應的DFS，與2號頂點相鄰的還剩一個1號頂點，1號頂點還沒有被訪問過，

第七個訪問1號頂點，與1號頂點相鄰的第一個頂點即2號頂點已經被訪問過，因此跳過2號頂點，與1號頂點相鄰的第二個頂點即5號頂點還沒有被訪問過，

第八個訪問5號頂點，與5號頂點相鄰的第一個頂點即1號頂點已經被訪問過，此時5號頂點訪問結束，

返回到1號頂點對應的DFS，與1號頂點相鄰的所有頂點全部訪問完畢，

所以繼續返回到2號頂點對應的DFS，此時與2號頂點相鄰的頂點全部訪問完畢，

最終該圖的深度優先遍歷結束，得到的遍歷序列為2、6、7、8、4、3、1、5：

5.總結：關于圖采用鄰接表存儲

五.深度優先生成樹：

下圖的兩個例子都是從2號頂點開始深度優先遍歷圖，左邊的例子基于之前第一個鄰接表，右邊的例子基于之前第二個鄰接表，由于鄰接表的不同，即使從同一個頂點開始深度優先遍歷，得到的遍歷序列也可能不同，：

深度優先遍歷的過程中也是在探索各條邊所連接的頂點的過程，

如果通過某一條邊找到某個頂點且該頂點還沒有被訪問過，此時就把這條邊標紅，通過某一條邊找到某個頂點且該頂點被訪問過則邊標黑，

如果只保留紅色的邊，把黑色的邊去掉，最終的圖就變成了一個沒有環的樹，

如果采用鄰接表存儲的圖，即便從同一個頂點出發進行深度優先遍歷，也有可能得到不一樣的深度優先遍歷序列，因此也會對應不一樣的深度優先生成樹：

六.深度優先生成森林：

如上圖，如果圖是非連通的，也就是說要調用多次DFS函數才能把圖深度優先遍歷完，每調用一次DFS函數，就會生成一棵深度優先生成樹，由于上述圖片的無向圖有兩個連通分量，所以需要調用兩次DFS函數，因此也會對應的生成兩棵深度優先生成樹：

上述圖片的兩棵深度優先生成樹就組成了深度優先生成森林。

七.圖的遍歷與圖的連通性：

1.無向圖：

對于無向圖而言，進行BFS或者DFS時，遍歷圖中調用BFS函數或者DFS函數的次數等于連通分量數。

如上圖，把上述圖片的圖進行BFS或者DFS時，由于該圖有3個連通分量數，因此需要調用3次BFS或者DFS才能遍歷完圖。

如果無向圖是連通圖即只有1個連通分量，所以只需要調用1次BFS或者DFS函數即可遍歷完圖。

2.有向圖：

比如從7號頂點出發進行BFS或者DFS，只需要調用一次BFS函數或者DFS函數即可遍歷完圖，其中一條遍歷序列為7、8、4、3、6、2、1、5；

比如從2號頂點出發進行BFS或者DFS，此時只能找到1、5號頂點（因為方向），所以無法調用一次BFS函數或者DFS函數就遍歷完圖。

特殊情況：有向圖是強連通圖（也就是從任何一個頂點開始都能找到到達其他所有頂點的路徑）