
一.復習:
1.生成樹:

對于一個連通的無向圖,假設圖中有n個頂點,如果能找到一個符合以下要求的子圖:
子圖中包含圖中所有的頂點,同時各個頂點保持連通,
而且子圖的邊的數量只有n-1條,
那么這樣的子圖就是生成樹,一個連通圖可能有多個生成樹。
2.廣度優先生成樹:

3.深度優先生成樹:

二.最小生成樹(最小代價樹):生成樹必須包含圖中所有的頂點
1.前言:

假設有一個城市叫P城,P城周圍規劃了學校、農場、電站、漁村、礦場,
各個地方之間有上圖所示的修路方案,其中數字表示修路的成本,比如修一條P城和學校之間的路需要1塊錢,修一條學校和礦場之間的路需要5塊錢,
現在為了節省P城的財政支出,沒有必要把所有的可行的道路都修一遍,
因此需要制定一個修路方案,這個方案要求所有地方都是連通的即各個地方之間是相互可到達的(各個地方之間不一定是相鄰的),但是成本又必須降到最低,此時有如下兩種方案:

左邊的方案可以使得各個地方連通,代價是20塊錢(圖片打錯了);
右邊的方案也可以使各個地方連通,但代價是16塊錢,
但是否有更便宜的方案呢?這就是最小生成樹(最小代價樹)要研究的問題。
對于帶權的連通圖,它可以有多個生成樹,我們要從所有的生成樹當中找出各個邊的權值之和最小即代價最小的那棵樹,這個樹就是最小生成樹。
2.概念:
注:最小生成樹研究的是帶權的連通無向圖。

3.特例:當帶權連通的無向圖的權值都為一個數
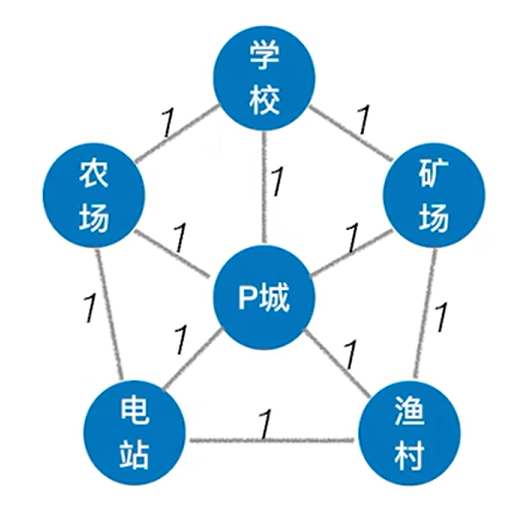
以上述圖片的帶權連通無向圖為例,可得出如下兩個生成樹:

由生成樹的概念可知這兩棵生成樹的邊都是5條(邊等于頂點總數減一,此時有6個頂點),由于每一條邊的權值都為1,因此這兩棵生成樹所有邊的權值之和都為5,
由此可知本例中帶權無向圖的任意一棵生成樹的所有邊的權值之和都為5,因此最小的權值之和為5,
結論:假設一個帶權連通無向圖的頂點數為V個,邊為E條,邊的權值都為a,
該圖的所有生成樹都只有(V-1)條邊,其權值之和為(V-1) * a,由此可知最小生成樹的權值之和為(V-1) * a,因為所有樹都一樣。
4.性質:

-
如果一個連通圖本身就是一棵樹(樹不存在環路),也就是圖中各個頂點連通但不存在環,那么這個圖的最小生成樹就是它本身->因為如果連通圖是樹時,那么它已經是生成樹了,而且無法再有更小的生成樹了,再有的話就會缺頂點,不符合生成樹的條件,所以此時這個圖的最小生成樹就是它本身
-
只有連通圖才有生成樹
-
對于非連通圖,只會有生成森林,因為非連通圖不止一個連通分量,生成的也就不止一個生成樹,最終就是生成森林(這里生成必須要包括圖中的所有頂點,不然不符合生成的條件)

5.總結:

三.求最小生成樹-Prim算法(普里姆算法):
1.例一:

以上述圖片為例,挑選圖中任意一個頂點,從該頂點出發構建生成樹:

如上圖,比如從P城這個頂點出發構建生成樹,之后每次將代價最小的新頂點納入生成樹,直到所有頂點都納入為止,
此時要構建的生成樹中只有P城這一個頂點,從P城出發,分別對比到達學校、礦場、漁村、電站、農場所需要的代價,可知從P城到達學校的代價最小,因此接下來要把學校這個頂點納入生成樹,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有P城和學校兩個頂點,
現在要從P城或學校出發,在農場、電站、漁村、礦場中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為4,如下圖:

意味著可以把礦場或者漁村納入生成樹中,
此時先把礦場納入生成樹,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校和礦場,
現在要從P城或學校或礦場出發,在農場、電站、漁村中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為2,如下圖:

意味著把漁村納入生成樹中,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校、礦場和漁村,
現在要從P城或學校或礦場或漁村出發,在農場、電站中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為5,如下圖:

意味著把農場納入生成樹中,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校、礦場、漁村和農場,
現在要從P城或學校或礦場或漁村或農場出發,在電站中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為3,如下圖:
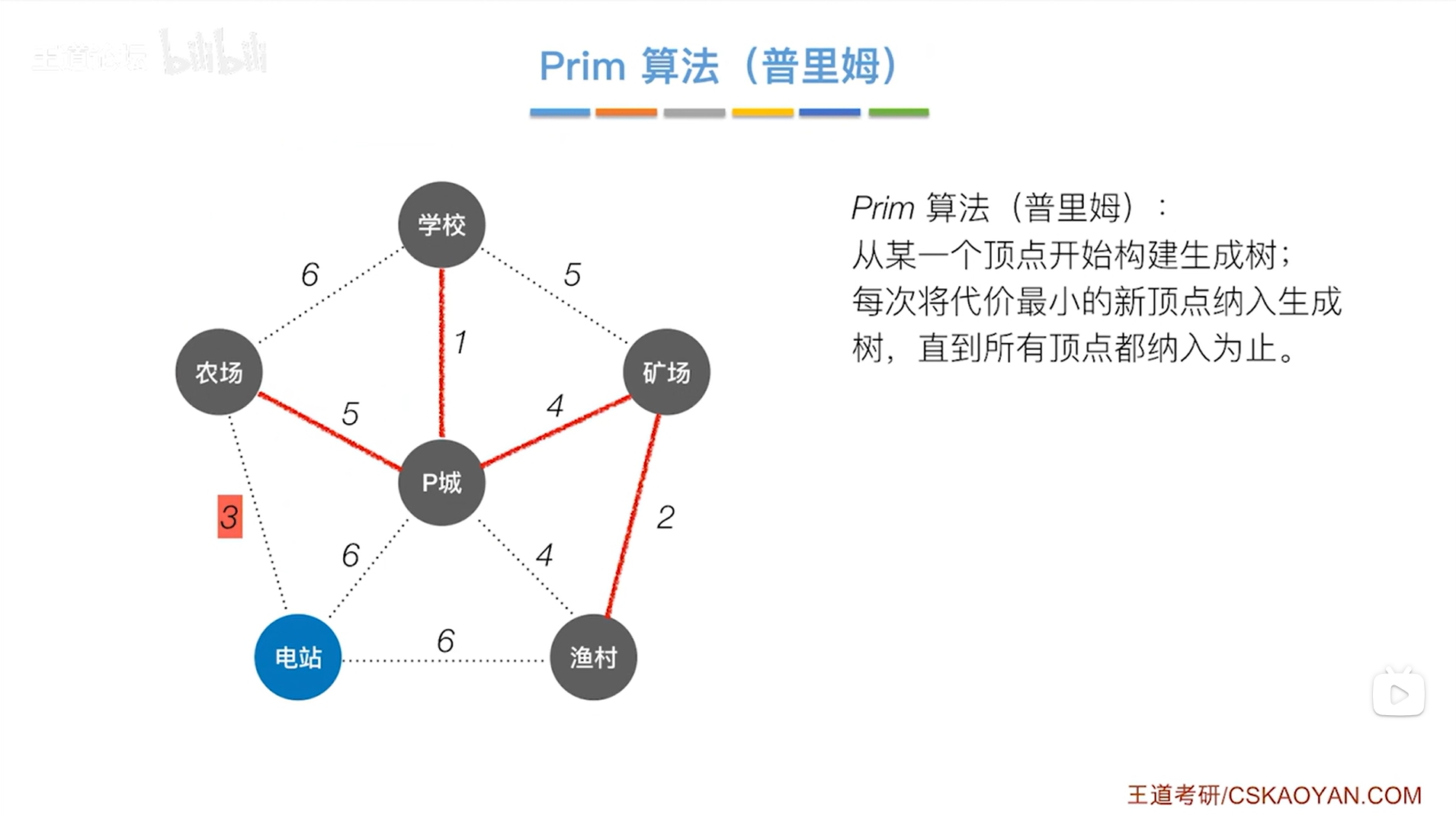
意味著把電站納入生成樹中,如下圖:

如下圖,最終得到了最小生成樹:

也就是說按照如上圖所得出的最小生成樹進行施工的話,只需要付15塊錢,也是最小代價。
2.例二:

以上述圖片為例,挑選圖中任意一個頂點,從該頂點出發構建生成樹:

如上圖,比如從P城這個頂點出發構建生成樹,之后每次將代價最小的新頂點納入生成樹,直到所有頂點都納入為止,
此時要構建的生成樹中只有P城這一個頂點,從P城出發,分別對比到達學校、礦場、漁村、電站、農場所需要的代價,可知從P城到達學校的代價最小,因此接下來要把學校這個頂點納入生成樹,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有P城和學校兩個頂點,
現在要從P城或學校出發,在農場、電站、漁村、礦場中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為4,如下圖:

意味著可以把礦場或者漁村納入生成樹中,
此時把漁村納入生成樹,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校、漁村,
現在要從P城或學校或漁村出發,在農場、電站、礦場中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為2,如下圖:

意味著把礦場納入生成樹中,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校、漁村、礦場,
現在要從P城或學校或漁村或礦場出發,在農場、電站中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為5,如下圖:

意味著把農場納入生成樹中,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中包括P城、學校、漁村、礦場、農場,
現在要從P城或學校或漁村或礦場或農場出發,在電站中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為3,如下圖:

意味著把電站納入生成樹中,如下圖:

如下圖,最終得到了最小生成樹:

也就是說按照如上圖所得出的最小生成樹進行施工的話,只需要付15塊錢,也是最小代價。
3.對比例一與例二分別得出的最小生成樹:

以上兩棵生成樹的最小代價都是15,
因此同一個圖可能有多個最小生成樹,雖然形態不同,但是這些最小生成樹的所有邊的權值之和都是一樣且最小的。
4.例三:

以上述圖片為例,挑選圖中任意一個頂點,從該頂點出發構建生成樹:

如上圖,比如從農場這個頂點出發構建生成樹,之后每次將代價最小的新頂點納入生成樹,直到所有頂點都納入為止,
此時要構建的生成樹中只有農場這一個頂點,從農場出發,分別對比到達學校、電站、漁村、礦場、P城所需要的代價,可知從農場到達電站的代價最小,因此接下來要把電站這個頂點納入生成樹,如下圖:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有農場和電站兩個頂點,
現在要從農場或電站出發,在漁村、礦場、學校、P城中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為5,如下圖,因此要把P城納入生成樹中:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有農場、電站、P城,
現在要從農場或電站或P城出發,在漁村、礦場、學校中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為1,如下圖,因此要把學校納入生成樹中:

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有農場、電站、P城、學校,
現在要從農場或電站或P城或學校出發,在漁村、礦場中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為4,如下圖,因此可以把礦場或漁村納入生成樹中,此時把礦場納入生成樹中(這里把漁村納入生成樹后得出的最小生成樹的最小代價一致):

如上圖,在當前生成樹下重復剛才的步驟,此時的生成樹中有農場、電站、P城、學校、礦場,
現在要從農場或電站或P城或學校或礦場出發,在漁村中選擇一個代價最小的頂點連到當前生成樹中,
由上圖可知最小的代價為2,如下圖,因此可以把漁村納入生成樹中:

最終得出了如上圖所示的最小生成樹,最小代價也是15,與例一、例二的最小代價一樣。
四.求最小生成樹-Kruskal算法(克魯斯卡爾):
實例:

執行過程:每次選擇一條權值最小的邊,使這條邊的兩頭連通(原本已經連通的就不選),直到所有頂點連通。
以上述圖片為例,一開始圖里的各個頂點都獨立存在,各個頂點之間不存在邊,所以用虛線標注,
現在從所有的虛線里挑出權值最小的一條,顯然權值最小的是1這條虛線,如下圖:

如上圖,1這條虛線的兩頭是P城和學校這兩個頂點,這兩個頂點此時還沒有連通,所以把這條虛線選中,使這兩個頂點連通,如下圖:

如上圖,繼續從所有的虛線里挑出權值最小的一條,顯然權值最小的是2這條虛線,如下圖:

如上圖,2這條虛線的兩頭是漁村和礦場這兩個頂點,這兩個頂點此時還沒有連通,所以把這條虛線選中,使這兩個頂點連通,如下圖:

如上圖,繼續從所有的虛線里挑出權值最小的一條,顯然權值最小的是3這條虛線,如下圖:

如上圖,3這條虛線的兩頭是農場和電站這兩個頂點,這兩個頂點此時還沒有連通,所以把這條虛線選中,使這兩個頂點連通,如下圖:

如上圖,繼續從所有的虛線里挑出權值最小的一條,顯然權值最小的是4這條虛線,如下圖:

如上圖,P城和礦場之間的虛線的權值、P城和漁村之間的虛線的權值都為4,現在選擇P城和礦場之間的虛線,P城和礦場這兩個頂點此時還沒有連通,所以把這條虛線選中(P城和漁村這兩個頂點此時也沒有連通,所以選這條虛線也可以),使這兩個頂點連通,最終P城、礦場、漁村、學校這幾個頂點就都連通了,如下圖:

如上圖,繼續從所有的虛線里挑出權值最小的一條,顯然權值最小的是4這條虛線,如下圖:

如上圖,此時權值為4的這條虛線的兩頭是P城和漁村,由于P城和漁村這兩個頂點已經連通了,所以這條虛線需要跳過不選,如下圖:

如上圖,繼續從所有的虛線里挑出權值最小的一條,顯然權值最小的是5這條虛線,如下圖:

如上圖,P城和農場之間的虛線的權值、學校和礦場之間的虛線的權值都為5,由于學校和礦場已經連通,因此學校和礦場之間的虛線不選,而P城和農場之間還沒有連通,所以應選中P城和農場之間的虛線,如下圖:

如上圖,至此,所有的頂點全部連通,Kruskal算法(克魯斯卡爾)結束。
如下圖,本例采用Kruskal算法(克魯斯卡爾)得出的最小生成樹的最小代價為15,與用Prim算法(普里姆算法)得出的結果一致:

五.Prim算法(普里姆算法) v.s. Kruskal算法(克魯斯卡爾):
假設圖中有V個頂點、E條邊:

對于Prim算法(普里姆算法),每一次是選擇一個頂點開始;
對于Kruskal算法(克魯斯卡爾),每一次是選擇一條邊開始;
因此這兩個算法所表現出的時間復雜度也就不一樣,
Prim算法(普里姆算法)的時間復雜度只與頂點的個數有關,適用于邊稠密圖即邊多的圖(因為邊多的話頂點相對少一些),
Kruskal算法(克魯斯卡爾)的時間復雜度只與邊的個數有關,適用于邊稀疏圖即邊少的圖(因為邊越少越能在短時間完成)。
六.Prim算法的實現思想:
1.實例:

以上述圖片為例,假設從v0頂點開始,設置isJoin數組和lowCost數組:
isJoin數組用于記錄圖中的頂點是否被加入正在組建的生成樹中,由于剛開始v0已經在生成樹中,所以v0在isJoin數組的值為true(上述圖片標記為勾),其余的頂點沒有加入生成樹中,因此其余的頂點對應的值都為false(上述圖片標記為叉);
lowCost數組用于記錄把這些頂點加入到已經組建的生成樹里所需要花費的最低代價->最開始選中了v0,
由于v0與v0之間不存在邊,所以v0對應的lowCost數組的值為0,
由于v0與v1之間有一條邊,這條邊的權值為6,因此把v1加入到組建的生成樹中所需要付出的最低代價是6,所以v1對應的lowCost數組的值為6,
由于v0與v2之間有一條邊,這條邊的權值為5,因此把v3加入到組建的生成樹中所需要付出的最低代價是5,所以v2對應的lowCost數組的值為5,
由于v0與v3之間有一條邊,這條邊的權值為1,因此把v2加入到組建的生成樹中所需要付出的最低代價是1,所以v3對應的lowCost數組的值為1,
而v4與v5這兩個頂點和v0之間都沒有直接相連的邊,所以就目前來看,暫時無法把v4、v5放到組建好的生成樹中,因此v4與v5對應的lowCost的值都用無窮記錄,也可以用別的記錄。
如下圖,開始進行第一輪處理:

首先需要檢查isJoin數組和lowCost數組,最終找出一個還沒有被加入生成樹且代價最低的頂點,
由上述圖片可知,v3頂點沒有加入生成樹中且代價最小,因此把v3頂點加入生成樹中,如下圖:

如上圖,要把v3頂點在isJoin數組中對應的值修改為true即勾,表示已加入生成樹中,繼續如下圖:

如上圖,需要循環遍歷lowCost數組,更新還沒加入的各個頂點對應的lowCost值,
現在加入了v3這個頂點之后,對于其他的還沒有被加入生成樹的頂點,接下來加入生成樹的代價有可能會改變,
因為生成樹中相較于一開始多了個v3頂點,最開始只有v0頂點時加入v1頂點最低代價為6,現在多了個v3頂點,加入v1頂點的最低代價為5,顯然小于6,因此接下來如果要把v1加到生成樹中,所需要付出的最低代價就從6變成了5,
因此把v1對應的lowCost值修改為5,同理現在
加入v2的最低代價為4,因此把v2對應的lowCost值修改為4,
加入v4的最小代價為6,因此把v4對應的lowCost值修改為6,
加入v5的最小代價為4,因此把v5對應的lowCost值修改為4,
由于v0與v3這兩個頂點已經加入到生成樹中,所以對應的lowCost值無需修改(因為之后不會再加入v0與v3這兩個頂點),
最終lowCost數組中的值依次為0、5、4、1、6、4,
如下圖:

如下圖,開始進行第二輪處理:原理與第一輪一樣

首先需要檢查isJoin數組和lowCost數組,最終找出一個還沒有被加入生成樹且代價最低的頂點,
由上述圖片可知,v2頂點和v5頂點都沒有加入生成樹中且代價都是最小的(代價都為4),因此v2頂點和v5頂點都可以加入生成樹中,但如果是從頭到尾去掃描lowCost數組中的元素,v2頂點是第一個被挑選并加入生成樹中的,如下圖:

如上圖,要把v2頂點在isJoin數組中對應的值修改為true即勾,表示已加入生成樹中,繼續如下圖:

如上圖,需要循環遍歷lowCost數組,更新還沒加入的各個頂點對應的lowCost值,
由上述圖片可知,加入v2頂點之后,
加入v1的最低代價為5,無需修改,
加入v4的最小代價為6,無需修改,
加入v5的最小代價為2,因此把v5對應的lowCost值修改為2,
由于v0、v3和v2這三個頂點已經加入到生成樹中,所以對應的lowCost值無需修改(因為之后不會再加入v0、v3和v2這三個頂點),
最終lowCost數組中的值依次為0、5、4、1、6、2,
如下圖:

如下圖,開始進行第三輪處理:

首先需要檢查isJoin數組和lowCost數組,最終找出一個還沒有被加入生成樹且代價最低的頂點,
由上述圖片可知,v5頂點沒有加入生成樹中且代價最小,因此把v5頂點加入生成樹中,如下圖:

如上圖,要把v5頂點在isJoin數組中對應的值修改為true即勾,表示已加入生成樹中,繼續如下圖:

如上圖,需要循環遍歷lowCost數組,更新還沒加入的各個頂點對應的lowCost值,
由上述圖片可知,加入v5頂點之后,
加入v1的最低代價為5,無需修改,
加入v4的最小代價為6,無需修改,
由于v0、v3、v2和v5這四個頂點已經加入到生成樹中,所以對應的lowCost值無需修改(因為之后不會再加入v0、v3、v2和v5這四個頂點),
最終lowCost數組中的值依次為0、5、4、1、6、2,
如下圖:

如下圖,開始進行第四輪處理:

首先需要檢查isJoin數組和lowCost數組,最終找出一個還沒有被加入生成樹且代價最低的頂點,
由上述圖片可知,v1頂點沒有加入生成樹中且代價最小,因此把v1頂點加入生成樹中,如下圖:

如上圖,要把v1頂點在isJoin數組中對應的值修改為true即勾,表示已加入生成樹中,繼續如下圖:

如上圖,需要循環遍歷lowCost數組,更新還沒加入的各個頂點對應的lowCost值,
由上述圖片可知,加入v1頂點之后,
加入v4的最小代價為3,因此把v4對應的lowCost值修改為2,
由于v0、v3、v2、v5和v1這五個頂點已經加入到生成樹中,所以對應的lowCost值無需修改(因為之后不會再加入v0、v3、v2、v5和v1這五個頂點),
最終lowCost數組中的值依次為0、5、4、1、3、2,

如下圖,開始進行第五輪處理:

首先需要檢查isJoin數組和lowCost數組,最終找出一個還沒有被加入生成樹且代價最低的頂點,
由上述圖片可知,v4頂點沒有加入生成樹中且代價最小,因此把v4頂點加入生成樹中,如下圖:

如上圖,要把v4頂點在isJoin數組中對應的值修改為true即勾,表示已加入生成樹中,
最終所有頂點全部加入到生成樹中,Prim算法結束。
2.時間復雜度分析:

上述例子中進行了好幾輪的處理最終得出最小生成樹,從代碼角度來看就是好幾輪的循環,
由于每一輪的循環都會選擇一個新的頂點把它放入生成樹中,假設圖中有n個頂點就需要n-1輪的循環,因為第一個頂點不需要循環,
而每一輪的處理當中又需要進行兩次循環遍歷,第一次循環遍歷所有的頂點來從isJoin數組和lowCost數組中找出未加入生成樹且代價最小的頂點,第二次循環遍歷所有的頂點來更新lowCost數組,所以每一輪的時間復雜度為O(2n),等價于O(n),
由于需要n-1輪循環,所以總的時間復雜度就是O( n * (n-1) ),等價于O( n * n - n ),等價于O( n * n ),
如果改為圖中有V個頂點,時間復雜度就是O( |V| * |V|)。
七.Kruskal算法(克魯斯卡爾)的實現思想:
1.實例:
如下圖,由于Kruskal算法(克魯斯卡爾)每次要選擇一條權值最小的邊,所以要先把各條邊按照權值遞增的次序進行排序:

如上圖,權值最小的邊是權值為1的這條邊,兩邊的頂點是v0和v3,所以上述圖片里的第一行數據中weight為1、Vertex1為v0、Vertex2為v3,該算法的執行過程就是把所有的邊都檢查一遍。

如上圖,第一條邊的權值為1,兩邊連的頂點是v0和v3,接下來就要檢查v0和v3是否連通,進行這個判斷用到了并查集(詳情見"5.15.并查集"),大致的思想就是剛開始要把所有的頂點分別看作是不同的集合,所以對于第一條邊的兩個頂點v0和v3,他們剛開始從屬于不同集合,也就意味著他們此時不連通,因此就可以把這條邊選中,如下圖:

此時v0和v3這兩個頂點就屬于同一個集合了,
如下圖,接下來進行第二輪的處理,權值為2的邊的兩頭為v2和v5,v2和v5此時不屬于同一個集合即v2和v5不連通,所以把v2和v5連起來,把v2和v5歸并為同一個集合:

如下圖,接下來進行第三輪的處理,權值為3的邊的兩頭為v1和v4,v1和v4此時不屬于同一個集合即v1和v4不連通,所以把v1和v4連起來,把v1和v4歸并為同一個集合:

如下圖,接下來進行第四輪的處理,其中一條權值為4的邊的兩頭為v2和v3,v2和v3此時不屬于同一個集合即v2和v3不連通,所以把v2和v3連起來,把v2和v3歸并為同一個集合:

如下圖,接下來進行第五輪的處理,其中一條權值為4的邊的兩頭為v3和v5,v3和v5此時屬于同一個集合即v3和v5連通,所以v3和v5之間的邊會跳過,不選中:

接下來的過程同理,最終把v1與v3連接后就得出最小生成樹,
如下圖,總之就是要把所有的邊都遍歷一遍,每當處理一條邊時,需要判斷這條邊所連接的兩個頂點是否從屬于同一個集合,如果不是,那就把這條邊選中,如果是,就不選中:

2.時間復雜度分析:
假設圖中共有e條邊:

每輪循環中判斷兩個頂點是否屬于同一個集合,要用到并查集,這個過程的時間復雜度詳情見"5.15.并查集",共e輪。
八.總結:










)
概述——從AWS開始)


)





