摘要：本文旨在開發一種基于有限元分析（FEA）和神經網絡（NN）計算的多尺度分層混合模型，通過將介觀尺度（骨小梁網絡層級）與宏觀尺度（全骨層級）耦合，模擬骨重建過程。由于全骨模擬（包括骨小梁層級的3D重建）耗時巨大，本研究僅在宏觀層面進行有限元計算，而通過訓練的神經網絡替代介觀尺度所需的有限元代碼，以快速預測骨小梁的形態與力學適應性。宏觀尺度的骨力學屬性根據介觀尺度神經網絡計算的形態與力學適應性結果進行更新。基于μ-CT影像的數字化建模技術和體素有限元分析被用于捕捉股骨頭介觀尺度下2 mm3的代表性體積元（RVE）。人工神經網絡的輸入數據包括骨材料參數、邊界條件及施加的應力，輸出數據為更新后的骨屬性（如彈性模量）和骨小梁參數（如體積分數）。據我們所知，這是首個結合有限元分析與神經網絡計算、快速模擬多層級骨適應性變化的模型。
核心目標：
開發多尺度耦合模型（宏觀FEA + 介觀NN），解決傳統全骨模擬（含骨小梁3D重建）計算成本高的問題，實現骨重建過程的高效跨尺度仿真。
方法框架：

宏觀尺度：利用有限元法（FEA）模擬全骨力學響應，獲取應力/應變分布及邊界條件。
介觀尺度：通過μ-CT影像構建2 mm3代表體積元（RVE），訓練神經網絡（輸入：材料參數、邊界條件、應力；輸出：更新骨屬性及骨小梁參數），替代傳統三維FEA，快速預測骨小梁網絡的適應性變化。
雙向耦合：宏觀FEA將力學狀態傳遞至介觀NN，NN預測微結構響應后反饋更新宏觀材料屬性，形成閉環優化。

技術創新：

首次耦合FEA與NN：突破傳統多尺度模擬依賴單一方法的局限，利用NN加速介觀計算（耗時從小時級降至秒級）。
數據驅動建模：基于μ-CT影像提取真實骨小梁微結構，結合體素有限元生成訓練數據，提升模型生物學真實性。
動態屬性更新：通過NN實時修正宏觀骨屬性（如彈性模量、密度），反映骨重建的適應性機制。

應用價值：

高效性：顯著降低計算成本，支持臨床場景（如骨質疏松治療規劃、植入物設計）中的快速力學評估。
多尺度預測能力：同時捕捉全骨宏觀力學響應與骨小梁介觀結構演變，為骨適應性機制研究提供新工具。
可擴展性：框架可推廣至其他生物組織（如軟骨、血管）的多尺度力學建模。

潛在挑戰：

數據依賴：NN性能受限于μ-CT數據質量與多樣性，需大規模標注數據集。
模型可解釋性：NN的“黑箱”特性可能限制其在臨床決策中的可信度。
三維擴展：當前宏觀FEA為二維簡化模型，未來需擴展至三維全骨仿真以提升精度。

1 引言

骨骼是一種分層組織的材料，其適應性在很大程度上取決于其小梁結構，隨著時間的推移可以通過對其形態和機械性能的變化進行評估（Tovar 2004; Yoo 和 Jasiuk 2006）。2004年，Poter 提出了用于骨骼的多尺度建模的分析方案，將其視為一種天然混合納米復合材料，以預測組成材料的個體特性。盡管所提出的模型對皮質骨的楊氏模量給出了與現有實驗數據良好的估計，但它無法提供關于應力分布和骨微結構演變的數據。Sansalone 等（2007）使用了一種二維多尺度建模方法來研究骨骼的機械性能。他們的方法提供了在給定尺度上的機械響應。Ghanbari 和 Naghdabadi（2009）采用了一種分層多尺度建模方案分析皮質骨，認為其是一種納米復合材料。定義了一個宏觀尺度和一個微觀尺度的邊界值問題。通過采用均勻化技術在這些尺度之間建立耦合。盡管在骨骼多尺度建模領域取得了進展，但仍缺乏整合不同尺度的骨結構信息及重塑過程的模型（Viceconti 等，2008）。骨重塑過程的計算模型必須解決多層次上的骨結構變化，從而允許對整塊骨骼進行更準確的描述（Adachi 等，1999; Fernandes 等，1999; Bagge 2000; Huiskes 等，2000; McNamara 和 Prendergast，2007; Hambli 等，2009）。該過程以分層方式在不同的時間和空間尺度上發生，交互現象連接著不同的尺度（Weiner 和 Traub，1992; Rho 等，1998; Tovar 2004; Yoo 和 Jasiuk 2006）。近年來，提出了多種數學模型來解釋和模擬重塑過程。雖然這些模型提供了有價值的見解，但到目前為止，它們僅通過基于理想化的二維或三維小梁結構的均勻化方法來解決骨結構/屬性的變化（Adachi 等，1998, 1999; Yoo 和 Jasiuk 2006; Fernandes 等，1999; Bagge 2000; Jacobs 2000; Sansalone 等，2007）。此外，在各種多尺度建模方法中，分層多尺度建模方法比均勻化方法在確定各個層次間相互作用方面更具優勢。最近，Leardini 等（2006），Viceconti 等（2007, 2008）開發了一種解剖功能多尺度超級模型，用于人類肌肉骨骼系統，能夠預測在常規物理負荷下的骨折風險。他們引入了一種隨機本構律來表示骨材料響應相對于位置和時間的變化。所提出的超級模型被構思為五個相互依賴的子模型的相互連接：連續性、邊界條件、本構方程、重塑歷史和失效標準。整個解剖功能超級模型被定義為一組程序化宏，用于預測特定個體的骨折風險。該模型的應用復雜，因為其基于對子模型的串行執行。此外，尚未提出將各個子模型集成到單一階段執行中的方案，這使得其在日常臨床使用中的應用既冗長又耗時。Jang 和 Kim（2010）開發了一種數值框架，計算確定骨重塑過程中皮質和小梁骨類型的相互作用和結構變化。他們構建了一種二維微有限元（μFE）模型，代表人類近端股骨的整個皮質骨和總小梁架構。研究的一個限制是，考慮了在介觀級別上的二維適應，因此無法捕捉到骨重塑過程的真實三維特性。

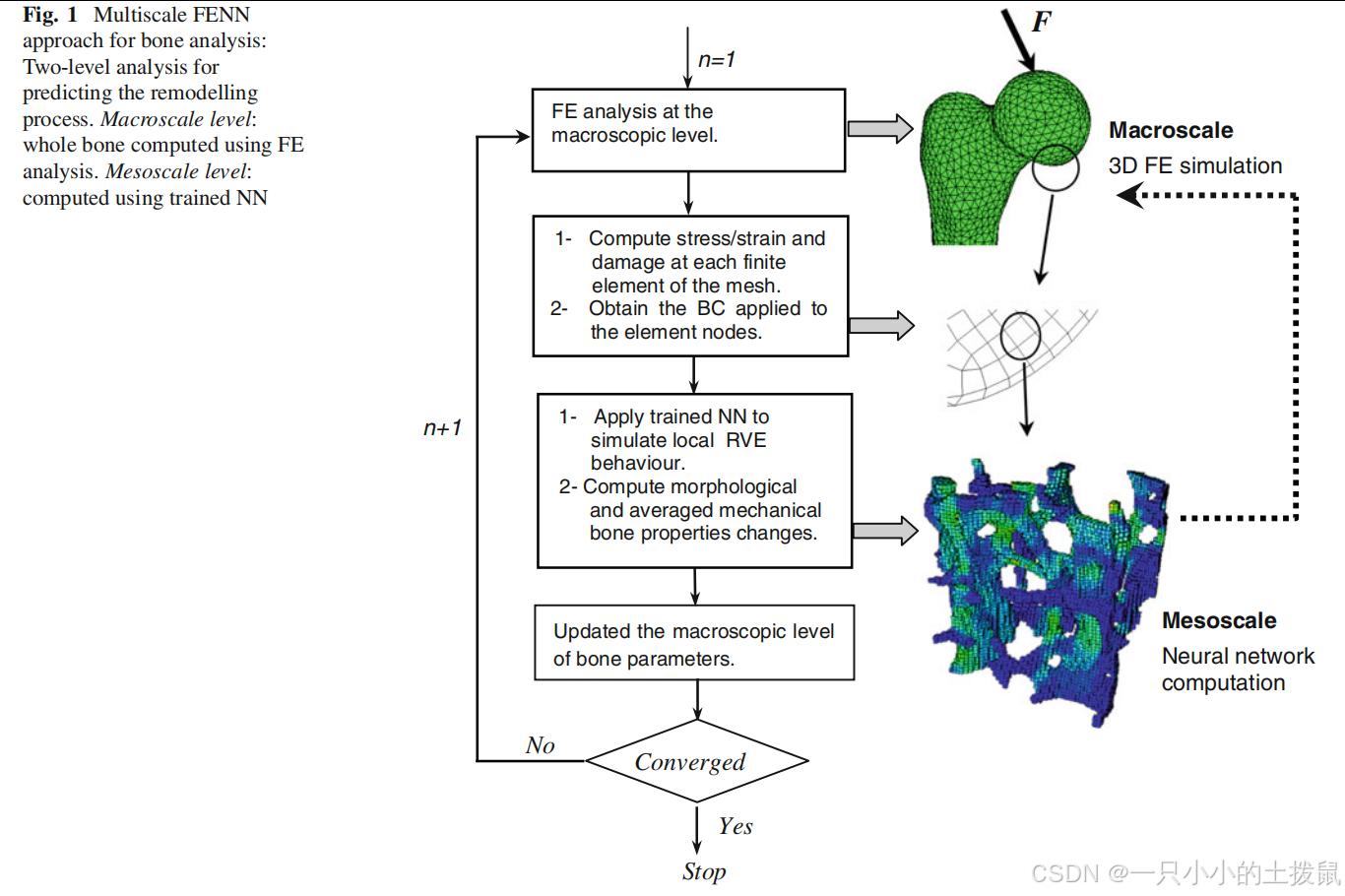
在本文中，我們描述了一種快速的多尺度方法，用于模擬骨重塑過程，采用二維有限元（FE）分析在宏觀層面，三維神經網絡（NN）計算在介觀層面。我們區分以下結構層次：宏觀結構（整體骨骼）和介觀結構（小梁架構）。從數值角度來看，組織（宏觀）尺度通過在每個有限元網格上求解宏觀分析后獲得的宏觀變量和邊界條件，將信息傳遞到介觀尺度。在介觀尺度上，將宏觀有限元結果得出的局部邊界條件應用于介觀骨模型，并通過訓練的神經網絡計算介觀模型響觀尺度將信息應。最后，介以更新后的材料性質的形式回傳給宏觀尺度。

我們使用數字圖像建模技術，通過μ-CT和體素有限元分析，在股骨頭的介觀水平上捕獲代表性體積元素（RVE）為2 mm3。人工神經網絡的輸入數據是一組骨材料參數、邊界條件和施加的應力。輸出數據是更新后的骨屬性和一些小梁骨因子。當復雜模型的數值分析耗時或不可行時，NN方法非常有用（Topping 和 Bahreininejad 1992; Jenkins 1997; Rafiq 等，2001; Unger 和 Konke 2008; Hambli 等，2006）。此外，NN模型可以用于整合從實驗數據和醫學圖像中提取的信息。該方法的另一個優點是，不同尺度之間的聯接階段以及逆計算的應用可以快速且輕松地進行（Jenkins 1997; Rafiq 等，2001）。

2 方法

提出的“混合有限元與神經網絡”（FENN）方法是一種模擬程序，其中將骨骼的連續體模型離散化為更小的子模型。經過訓練的神經網絡（NN）局部應用于確定小梁網絡中的任何結構和機械變化。然后將局部結果反饋到全局水平模型中。連續體模型的材料分布變化將影響應力和應變場的分布，從而影響后續迭代中每個介觀模型的機械刺激。FENN方法的示意圖如圖1所示。

在本研究中，介觀尺度的研究基于以40μm體素大小獲取的2 mm3均勻代表性體積元素（RVE）樣品的計算微位掃描（圖2）。介觀方法可以總結為以下五個步驟：

1. 針對不同組合的骨輸入進行RVE的有限元重塑模擬。
2. 對RVE輸出進行平均。
3. 步驟1和2提供以“實驗設計”（DoE）表格形式的訓練數據，用于NN訓練。
4. 基于數字DoE對NN進行訓練。
5. 將NN納入宏觀有限元模型，以鏈接介觀和宏觀尺度。

方法概述

• FENN 方法：結合有限元分析（FE）與神經網絡（NN）來模擬骨骼結構的重塑過程。

• 模型離散化：將連續體骨模型分解為更小的子模型，便于局部分析。

核心步驟

1. 有限元重塑模擬：對不同的骨輸入組合進行模擬，生成代表性體積元素（RVE）。

2. 輸出平均化：對各個RVE的模擬結果進行平均處理。

3. 訓練數據準備：生成實驗設計（DoE）表，為神經網絡的訓練提供數據。

4. 神經網絡訓練：基于前面步驟得到的數字DoE，對神經網絡進行訓練。

5. 模型集成：將經過訓練的神經網絡整合進宏觀有限元模型，以實現介觀與宏觀尺度之間的關聯。

研究數據來源

• 微位掃描：基于40μm體素大小的計算微位圖像，獲取2 mm3的均勻RVE樣品。

2.1宏觀尺度的有限元模型

模型中包含三種不同材料：骨小梁（松質骨）、皮質骨（密質骨）和骨髓。然而，與骨基質相比，骨髓的力學影響可忽略不計（Martínez-Reina等，2009）。
從結構上看，骨組織是一種具有復雜層級結構的復合材料。在連續介質層面，骨的有效力學性能取決于其結構，因此表現出各向異性行為。對于皮質骨，其孔隙率極低，各向異性主要由骨板層和骨單位方向控制；對于松質骨，孔隙率較高，各向異性的主要決定因素是骨小梁的取向。已有研究提出了多種各向異性本構模型以模擬骨的行為（Jacobs等，1997；Hart和Fritton，1997；Fernandes等，1999；Doblare和Garcia，2002；Martínez-Reina等，2009）。由于本研究聚焦宏觀尺度，為簡化計算，采用平均化的各向同性骨行為模型（Tovar，2004）。未來工作需擴展模型以納入各向異性和骨髓的影響。

宏觀尺度下皮質骨與松質骨的本構方程表示為：

其中，σij?為應力，εkl?為應變，aijkl?為各向同性彈性剛度張量。
宏觀模型中未考慮損傷效應，其耦合作用通過介觀尺度（骨小梁層級）的公式引入。此外，本研究未涉及皮質骨的重建過程，但宏觀有限元模型未來可擴展以描述皮質骨和松質骨的重建機制。

材料組成與簡化假設

材料類型：模型包含骨小梁（松質骨）、皮質骨（密質骨）和骨髓，但忽略骨髓的力學貢獻。
簡化處理：在宏觀尺度下，假設骨為各向同性材料（忽略實際各向異性），以降低計算復雜度。

骨結構的各向異性特征

皮質骨：低孔隙率（<10%），各向異性由骨板層排列和骨單位方向主導。
松質骨：高孔隙率（50-90%），各向異性由骨小梁網絡取向決定。

宏觀本構模型

本構方程：采用線性彈性各向同性模型（式1），彈性剛度張量aijkl?由平均化材料參數定義。
局限性：當前模型未考慮骨重建引起的材料非線性（如塑性變形或黏彈性效應）。

損傷與重建的跨尺度處理

損傷機制：損傷僅在**介觀尺度（骨小梁層級）**引入，通過微結構失效（如骨小梁斷裂）影響宏觀力學響應。
重建過程：當前模型僅模擬松質骨重建，未來需擴展至皮質骨。

2.2 用于神經網絡訓練的介觀尺度有限元模型

骨小梁的有效力學特性被建模為彈性各向同性行為，并耦合了應變與微損傷刺激的損傷機制（McNamara和Prendergast，2007）。其本構關系表示為：
σij?=(1?D)aijkl?εkl?(2)
其中，aijkl? 為各向同性彈性剛度張量。
對于純彈性應變下的高周疲勞問題（忽略熱耗散與機械耗散的耦合），Chaboche（1981）提出了非線性損傷模型：
D=1?(1?(Nf?N?)1?α1?)1+β1?(3)
式中，α 和 β 為材料參數，Nf? 為失效循環次數，由Martin等（1998）提出的公式確定：
Nfc?=1.479×10?21Δε?10.3（壓縮載荷）(4a)
Nft?=3.630×10?32Δε?14.1（拉伸載荷）(4b)
其中，Δε 為施加的微應變幅值。
骨密度的動態變化由以下方程組描述（Hambli等，2009）：
dtdρ?=αR?(S?SR?)若?S<SR?(5a)
dtdρ?=0若?SR?≤S≤SF?(5b)
dtdρ?=αF?(S?SF?)若?SF?<S<SD?(5c)
dtdρ?=αD?(S?SD?)若?S≥SD?(5d)
式中，ρ 為骨密度，t 為時間，S 為應變-損傷耦合刺激函數；αR?、αF? 和 αD? 分別表示骨吸收速率、骨形成速率和損傷吸收速率；SR?、SF? 和 SD? 分別為骨吸收、骨形成和損傷吸收的刺激閾值。
刺激函數 S 由骨細胞力學感知模型定義（Mullender和Huiskes，1995）：
S(x,t)=i=1∑Noc??fi?(x)μi?Si?(6)
其中，μi? 為骨細胞 i 的機械敏感性，Noc? 為骨細胞數量；fi?(x) 為空間影響函數：
fi?(x)=exp(?d0?di?(x)?)(7)
式中，di?(x) 為骨細胞 i 與骨表面位置 x 的距離，d0? 為歸一化因子。局部刺激值 Si? 由應變-損傷能量密度定義（Hambli等，2009）：
S=21?ρ(1?D)σij?εij??(8)
骨密度的更新通過前向歐拉法近似：
ρit+Δt?=ρit?+Δρi?(9)
局部彈性模量 E 由下式計算（Hambli等，2009）：
E=C(1?D)ργ(10)
式中，C 和 γ 為實驗標定常數。
代表體積元（RVE）的輸出變量通過體積平均化處理（Ghanbari和Naghdabadi，2009）：
yiRVE?=V0?1?∫VO??yi?dV(11)
其中，V0? 為RVE參考域體積，yi? 為每個有限元位置的輸出變量。

材料模型：

骨小梁被視為彈性各向同性材料，但引入損傷因子 D 反映微裂紋與疲勞效應（式2）。
損傷演化通過非線性方程（式3）描述，與載荷循環次數 N 和應變幅值 Δε 相關（式4a-b）。

骨密度動態機制：

骨密度變化分為四階段（式5a-d）：吸收（S<SR?）、平衡（SR?≤S≤SF?）、形成（SF?<S<SD?）和損傷修復（S≥SD?）。
刺激函數 S 由骨細胞感知的局部應變-損傷能量密度驅動（式6-8），空間影響隨距離指數衰減（式7）。

模量更新與跨尺度關聯：

彈性模量 E 與密度 ρ 的冪次關系（式10），受損傷 D 和實驗參數控制。
RVE平均化（式11）將介觀局部響應（如模量、密度）傳遞至宏觀模型，實現多尺度耦合。

應用與局限：

優勢：模型通過耦合損傷與骨重建機制，精確模擬骨小梁力學響應及適應性變化。
挑戰：參數標定（如 C,γ,α,β）依賴實驗數據；各向同性假設忽略骨小梁方向性特征。

2.3 用于神經網絡訓練的實驗設計準備

根據第2節所述的FENN（有限元-神經網絡）方法，通過微斷層掃描（μ-CT）成像、有限元仿真及代表體積元（RVE）平均化（步驟i和ii）生成神經網絡的訓練數據（步驟iii）。實驗設計分為兩個獨立問題：

宏觀尺度有限元分析：通過不同載荷、方向和頻率的單腿站立模擬，確定網格中每個有限元的邊界條件（應力幅值、方向）。
介觀尺度RVE模擬：將宏觀結果（應力幅值、方向、頻率）作為局部邊界條件輸入μ-CT體素有限元模型，執行100組RVE骨重建模擬。

輸入變量：

應力幅值（4個水平）
應力方向（5個水平，隨骨位點變化）
載荷頻率（5個水平，基于日常活動）
輸出變量：平均骨密度（ρ）、平均損傷（D）、平均彈性模量（E）、平均刺激（S）——這些參數是臨床評估骨質量的關鍵指標（Keyak等，2001；Bessho等，2007）。

實驗設計：

采用全因子組合（4×5×5），生成100組實驗（圖3）。
每組合對應一次RVE模擬，總計算時間約27小時（雙核2 GHz計算機）。

擴展性：當前模型可納入更多骨材料變量（如各向異性參數、熱力學耦合效應）以捕捉復雜骨行為。

實驗設計流程：

宏觀分析：獲取邊界條件（應力幅值、方向、頻率），覆蓋不同載荷場景。
介觀模擬：基于μ-CT數據生成100組RVE響應數據，作為NN訓練集。

輸入輸出定義：

輸入：應力幅值（4級）、方向（5級）、頻率（5級），反映實際生理載荷多樣性。
輸出：骨密度、損傷、模量及刺激（臨床骨質量核心指標）。

數據規模與計算成本：

全因子設計生成100組數據，覆蓋多因素交互效應。
計算耗時27小時（雙核2 GHz設備），凸顯傳統FEA的高成本，驗證NN替代的必要性。

臨床與工程意義：

臨床適用性：輸出參數（如E、ρ）直接關聯骨強度評估，支持個性化骨折風險預測。
擴展潛力：可納入更多變量（如骨小梁取向、多軸應力狀態）提升模型預測能力。

關鍵創新：通過系統性實驗設計，將多尺度骨重建的復雜力學-生物學耦合問題轉化為神經網絡可學習的輸入-輸出映射，為高效跨尺度仿真奠定數據基礎。