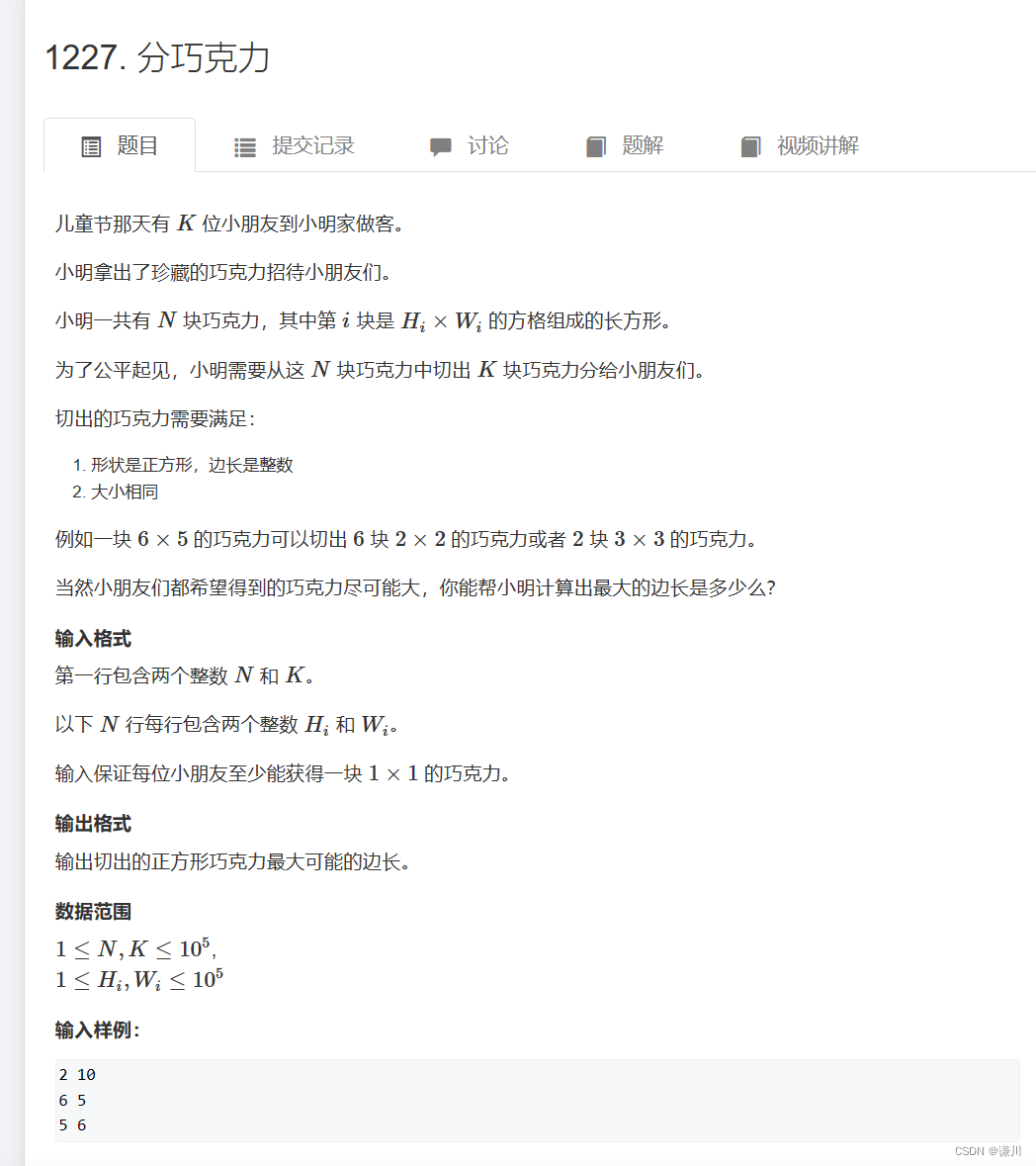
/*
分巧克力 解題思路?
二分?
直接檢查看答案是否符合題目條件
對于一塊邊長分別為x 和y的巧克力\\
假設我們輸入檢查的數為k?
其能分割成的 k*k 的巧克力的塊數為
(x/k)*(y/k)
因為c++里面的除法是下取整的所以我們不用考慮奇偶數 是否能整除

將每一塊巧克力能分成的k*k的巧克力塊數加上計數器
一旦計數器超過了孩子數 我們就返回true;
如果check 不通過的話 可能是分的太大了
所以答案小于mid
?于是我們讓r=mid-1
?如果check通過
?則答案>=mid 所以我們讓l=mid ??
重點 討論邊界情況
例如案例中?
2 10
6 5
5 6

輸出2?
當 l指向2 r指向3?
mid=(l+r)>>1;的話 mid 是2?
此時check可以通過?
但是l=2,r=3;
如果還是l=mid=2則陷入死循環
于是 我們讓mid=(l+r+1)>>1
讓其進行上取整
則 mid=3;
check不通過?
此時 r=mid-1=l；
退出循環
?
輸出l或者r即可?
?
*/?

代碼

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+10;
struct node{
?? ?int x;
?? ?int y;?? ?
}a[N];
int n,k;
bool check(int p){
?? ?int cnt=0;
?? ?bool flag=false;
//?? ?cout<<"p is "<<p<<endl;
?? ?for(int i=0;i<n;i++){
?? ??? ?cnt=cnt+(a[i].x /p)*(a[i].y /p);
?? ??? ?//cout <<cnt<<endl;?
?? ??? ?if(cnt>=k){
?? ??? ??? ?flag= true;
?? ??? ??? ?break;
?? ??? ?}
?? ??? ?
?? ?}
?? ?return flag;
}
int main(){
?? ?cin>>n>>k;
?? ?int r=0;
?? ?for(int i=0;i<n;i++){
?? ??? ?cin>>a[i].x >>a[i].y;
?? ??? ?if(a[i].x >a[i].y ){
?? ??? ??? ?if(a[i].x >r){
?? ??? ??? ??? ?r=a[i].x ;
?? ??? ??? ?}
?? ??? ?}else{
?? ??? ??? ?if(a[i].y >r){
?? ??? ??? ??? ?r=a[i].y ;
?? ??? ??? ?}
?? ??? ?}?? ??? ?
?? ?}
//?? ?cout<<r<<endl;
?? ?int l=0;
?? ?while(l<r){
?? ??? ?int mid=(l+r+1)>>1;
?? ??? ?//cout<<mid<<endl;
?? ??? ?if(check(mid)){
?? ??? ??? ?l=mid;
?? ??? ?}else{
?? ??? ??? ?r=mid-1;
?? ??? ?}
?? ??? ?//cout<<"l is"<<l<<endl<<"r is "<<r<<endl; ?
?? ?}
?? ?cout <<l;
?? ?return 0;?
}