目錄

插入排序：

核心思想：

時間復雜度：

冒泡排序：

核心思想：

時間復雜度：

希爾排序：

核心思想：

時間復雜度：

選擇排序：

核心思想：

時間復雜度：

堆排序：

核心思想：

時間復雜度：

快速排序：

霍爾版本：

核心思想：

快速排序小區間優化：

快速單趟排序改進思路1：挖坑法

快速單趟排序改進思路2：前后指針法

非遞歸快速排序：

所有排序的源碼：

頭文件

實現文件：

測試文件：

---

插入排序：

核心思想：

前面的數據有序，再將后一個數據插入前面的數據，就是一直保證前面的是有序的
例如：前1個有序、前2個有序、前3個有序、塞納4個有序。。。以此類推，最后n個數據全部有序

在已經排序好的系序列內插入值
先單趟，再多趟?

使用順序表第一個位置記錄數據個數很不好，例如哨兵的設計，因為數據的個數和數據的類型不一致，假設數據類型是char

設計數據結構不要感覺，如果感覺可以，那么可以的理由是什么；如果感覺不可以，那么不可以的理由是什么，不可以似是而非
要有具體的理由，而不是空憑感覺，有充分的理由，據具體的分析，好為什么好？有理有據

該種算法在順序有序或者接近有序效率比較高，但是逆序效果就會非常差,注意，這個特點很重要

寫排序算法，先單趟控制，不要一來直接整體控制，比較復雜，不好把握

時間復雜度：

最壞O(n^2)
最好O(n)

冒泡排序：

核心思想：

每一趟都保證將最大的數據放到最后一個位置
每一次兩兩比較,(升序)前一個比后一個大,交換位置，再比較后兩個數據,前一個比后一個大,再交換
? ? ? ? ? ? ? ? ? 在第一躺的交換就將所有的數據進行了一次遍歷比較，保證了將最大的數據放到最后面
? ? ? ? ? ? ? ? ? 再在此基礎上進行第二躺的比較，目的在于將第二大的數據放到最后的位置

對于冒泡排序和插入排序的區別：
冒牌排序無論是有序、亂序還是逆序，都是嚴格的等差數列
但是對于插入排序來說，除非是最壞的情況，基本都難以達到等差數列的量級，因為中間的交換次數會少于最多的次數

時間復雜度：

都是O(n^2)
? ? ? ? ? ? ? ? ? ?

希爾排序：

核心思想：

1、預排序（接近有序）：核心思想是讓小的數據盡快往前，大的數據盡快往后
2、直接插入排序
完成預排序之后，整個序列就已經接近于有序了，再進行插入排序

gap代表有多少組
隨著預排序的進行，會逐漸接近有序，后面挪動的就少了

預排序：
一組一組排序：先第一組，再控制gap躺
?多組并排：直接++i，不用分組，直接對間隔為gap的兩個數據之間進行插入排序，每一次都是一次數據有限的插入排序。理解清楚

先控制單趟，假設[0,end]是有序的，從end位置開始，從end+1往前進行對比排序，寫完單趟，再對整體進行控制

控制單趟：對前end位置循環對比，這是一組；再對下一組進行比較。對gap分組的一整個數據組進行排序，這算作一趟
再整體：整個數組分成gap組，對每個gap組進行單趟排序

時間復雜度：

平均下來是O(n^1.3)? (非常叼)

選擇排序：

核心思想：

在整個序列選出最小值和最大值，最小值放在左邊，最大值放在右邊，然后依次再選出次小的和次大的。

先控制單趟，然后再整體控制，將區間往中間縮小
選擇排序：遍歷選擇出最大的和最小的，然后將最大的放在后面，最小的放在前面；這就是單趟
然后，begin++，end--，縮小數組序列的間隔，因為最后的位置已經排序好了，因此縮小范圍，在還未進行排序的序列組內繼續進行上述的邏輯，挑出該組最大的和最小的進行操作。?

但是注意有一個坑：例如，當最大的值在第一個位置，那么選出最小的值的時候就會將兩者交換，但是下標沒有變化，此時已經將最小的值交換到了第一個位置，然而maxi的位置依舊指向第一個位置，那么，此時選出最小值的操作已經結束，但是找到最大值的操作就會出現錯誤，因為此時maxi指向的第一個位置已經不是最大值了，而是變化最小值了，交換就會出現錯誤。
當此時再堆maxi進行交換，就會出現將第一個最小值和最后一個位置交換，結果導致，最小的在最后，最大的在某個位置，序列全亂，完全沒有達到排序的效果
怎么解決這個問題？
很簡單，進行一個if判斷即可
maxi的值被改變，maxi的值應該是mini的位置，更新一下maxi = mini即可
因為交換第一個位置的時候，第一個位置是maxi，但是交換后，第一個位置已經被換成了min值，而最大值也被換到了mini的位置，所以此時最大值在mini的位置，此時更新一下maxi的位置即可

時間復雜度：

O(n^2)
因為無論是有序還是無序，無論交換與否都需要每次選出最大最小，所以，即使是有序時間復雜度依舊是O(n^2)

堆排序：

核心思想：

首先將數據進行建堆，然后將堆頂和最后的位置交換，再將堆頂向下調整。

向下調整建堆：倒著往上調整，而葉子節點是不需要向下調整的，所以調整位置從最后一個節點的父親節點開始向上，逐個進行向下調整
我們的數據序列在物理結構上是一個數組，邏輯上是一個二叉樹，從最后一個節點的父親節點開始，依次向前，對數組的每一個數據進行向下調整，這樣就保證了每一個節點都進行了向下調整建堆
因此，比較重要的是向下調整的邏輯：
從堆頂開始，和左右孩子進行比較，假設法，首先假設左孩子是符合條件的值，再對左后孩子的值進行比較，選出合適的孩子值，這是一個比較，子節點和父親節點進行交換，再依次更新父節點和孩子節點，再考慮結束條件即可。當end為0時，執行向下調整，說明就剩下一個數據了，不需要進行調整了。

假設數組的大小為size，那么數組的下標范圍是【0，size-1】
如果條件為<size，那么正好

時間復雜度：

O(NlogN)??

快速排序：

霍爾版本：

核心思想：

找一個數據key，比key小的在左邊，大的在右邊，最后key的位置在序列的位置即定

例如說，左邊有三個比key小的，那么key就在第四個位置
左邊有4個比key小的，那么可以就在第五個位置
也就是說，當把所有比key小的放在左邊，比key大的放在右邊，那么最終即使是排好序的序列里，key的位置依舊是這個位置
那么，再把左右兩邊的序列變化有序的，那么整體就是有序的了

單趟：先選擇第一個位置為key，然后在整體位置上，先找到右邊比較小的值，再找到左邊比較大的值，進行交換，再繼續進行查找大小值
但是，有一個坑：即while（left < right）的判斷條件不是if，l和R是動態變化著的，就有一種可能，即右邊已經找到了比較小的值，然后左邊開始從當前位置向前查找大的值，但是都沒有，那么就會一直跑到right的右邊
因為內部并沒有判斷，得完成了右邊小值和左邊大值的尋找結束才會進行判斷，此時，right在左邊，left在右邊，再交換，就出錯了。所以，在內部就需要多進行一個判斷，即left < right

當進行第一次key排序好位置之后，要對key的左邊和右邊進行處理
怎么處理？
類似一個二叉樹的遞歸過程
根（key）、左子樹（區間）、右子樹（右區間）
先對左邊的區間同上一樣的處理，只是此時的區間變成了【begin,keyi - 1】，對該區間進行key排序
再對右邊的區間同上一樣的處理，只是此時的區間變成了【keyi + 1, ? end】，對該區間進行key排序
什么時候條件結束？
當左子樹或者右子樹只有一個節點，即只剩下一個數據的時候，說明已經遞歸到最底層了
即，begin == end

但是，還有一個坑：就是當右邊遇到一個和key相等的值會停止，左邊也遇到一個和key相等的值也會停止，二者進行交換，交換過后；再繼續下一個循環，可是，當前位置的right指向的是從左邊left換過的key值，
當前位置的left指向的也是剛剛right交換過來的key值；那么再進行循環，還是會停止再當前的位置，兩個位置循環交換，循環找，循環停，陷入死循環。
為什么會出現這樣的情況？
因為，小的放在左邊，大的放在右邊
但是，相等的放在哪里？
似乎我們沒有進行特殊的處理，僅僅只是對大的和小的進行了處理
因此，我們需要將相等的值也考慮進去
相等的值，放在左邊和右邊，都無關緊要。
因此，在右邊找小值的時候，遇到和key相等的值，不管，繼續往左邊
同樣，在左邊找到大值得時候，遇到和key相等得值，不管，繼續往右邊

還有一個坑：當有序的情況下，其實開始位置用begin+1是有問題的，因為是有序的，右邊的right往左邊找小值，因為有序所以會一直往左邊找，直到遇到left，但是我們初始的位置是begin+1位置
那么就會在begin+1的位置相遇，就會導致begin和begin+1位置進行交換，但是我們的數據本身就是有序的，結果你交換了，反倒打亂了順序，不符合預期，所以初始位置要從begi位置開始
從begin位置開始，就可以避免這種情況，因為相遇的位置就是key位置本身，自己和自己交換，不影響序列的有序性

但是在有序的情況下，快排的效率是非常低的。因為我們選定key，例如一個有序序列，key是從第一個位置依次往后，那么就會導致，右邊的right找小，一直都找不到，需要從頭到尾遍歷一遍，相當于一個冒泡了
相反，如果我們每次選擇的key是一個中間值，那么整體的效率就會變得高效的多，時間復雜度是N*logN，因為類似于二叉樹，n個數據有logN層，每一層有n個。
那怎么解決這個問題呢？
導致這個問題的根節點在于，選定第一個位置作為key
那么，我們只需要改變這個key即可
那么是不是意味著我們要將整個的單趟操作重寫一遍呢？
不用
我們只需要將比較合適的數據和第一個位置的key進行交換即可，這樣就不需要重寫單趟邏輯
而且，這樣的寫法，本質上只是將key換成了一個更合適的值而已，其他都沒有變
那么問題來了：怎么選擇一個合適的key值呢？
第一種方法：從數據中隨機選一個值
第二種方法：三數取中，即第一個、最后一個、中間值，取中間值。邏輯是，選擇不是最大的，也不是最小的值做key，可以做到近似二分，效率更高。

為什么相遇左邊一定比右邊的大？：因為只有兩種情況
1、R遇L
為什么相遇位置一定比key小？因為右邊先走，當left找到大的，right找到小的，交換位置，交換位置后此時left的值是比key小的，而right是比key大的，此時繼續再剩下的序列中ringht尋找比key小的值，直到相遇，將key和相遇位置交換，此時是right動，而在最后的一個過程中，一定是right往左邊尋找，此時沒有找到比key小的，就會直接找下去直到遇見left位置，交換位置
2、L遇R
當right已經找到了一個比key小的值的時候，輪到左邊的left找比key大的值，但是沒有，就會和right相遇，即相遇位置依舊是比key小
以上兩種相遇方式保證了不論是那種相遇位置值都比key要小，但是關鍵是right先走

Debug版本本質是往代碼文件錄入很多調試信息，因此單個棧幀會比較大（所以棧容易溢出）
Release版本優化很多，例如一些中間一些沒必要的步驟優化了（速度更快，棧也更多）

快速排序小區間優化：

快速排序遞歸對于小區間的排序付出的代價是比較大的，我們可以在小區間使用插入排序對區間進行排序，這種方法叫小區間優化
為什么說代價比較大呢？
例如最后幾層，有7個值，按照我們的遞歸寫法，我么需要建立幾個函數棧幀？

7個函數棧幀，代價是比較大的。
而且如果是比較極端的情況，一個滿二叉樹，那么，最后幾層的節點會非常的多，需要建立大量的函數棧幀，消耗代價是比較大的。
所以，考慮將這部分進行局部優化
快排類似于二叉樹的遍歷，而滿二叉樹的下面三層幾乎占據整個數據序列的絕大多數，因此插入排序用于最后的3~4層的排序減少了很多遞歸
但是事實上，這個區間優化的效果并不是很明顯，所以也不是很有必要，看你自己需求

上面我們說的是霍爾版本的快速排序，你會發現很麻煩，需要注意的點很多，稍不注意就會寫錯，所以我們有以下幾個改進的方法：

快速單趟排序改進思路1：挖坑法

核心思想：在key位置首先挖一個坑，R往左邊找，找到比key小的值，將該值填到key的位置，R所在位置為新的坑

那么什么叫做挖坑呢？就是把key的值記錄下來，因為記錄下來了，就可以進行覆蓋，那么相當于key的位置就空出來了，形象的說，我們將之視為一個坑位。
而后L開始向右找比key大的值，找到后將該值放到右邊R所在位置的坑，此時L所在位置又成為一個新的坑，如此反復，最后在而這相遇的位置將key填入，一趟快速排序完成，就保證了key的左邊都是比key小的，右邊都是比key大的
對于該key值得單趟排序完成，接下來，再對左區間和右區間進行如上單趟排序即可，如此遞歸到結束。這就是挖坑法的所有邏輯。

快速單趟排序改進思路2：前后指針法

核心思想：依舊是將小的放在前面，大的放在后面（最推薦的寫法）

單趟排序：
前指針perv，后指針cur，key是第一個位置的值，
首先cur向右邊走，cur的目的在于找比key小的值，沒找到，繼續向右；
如果找到了，那么說明什么？
說明prev和cur之間的值都是比key大的值
然后，交換位置，把++prev 和 cur位置進行交換
此時，從視覺上看，就像推箱子，這個箱子就是比key大的值的區間
這個區間是【prev,cur】
區間的左邊都比key小，右邊都比key大
那么，當時cur走到最后的位置的時候，就是把大于key的值區間推到了最后
到此，將prev 和 key位置的值進行交換即可，整個單趟排序結束。

整體控制：
快速排序，只要把單趟寫好了，剩下的就是控制整體的區間問題，整個很簡單。
【begin，keyi - 1】keyi 【keyi + 1, end】
然后進行遞歸，先左區間，再右區間
結束條件是當begin >= cur
為什么結束條件是這個呢？
因為，當左邊只有一個值時,begin == keyi
當右邊沒有值時，右邊的end就是keyii，keyi + 1 > keyi?

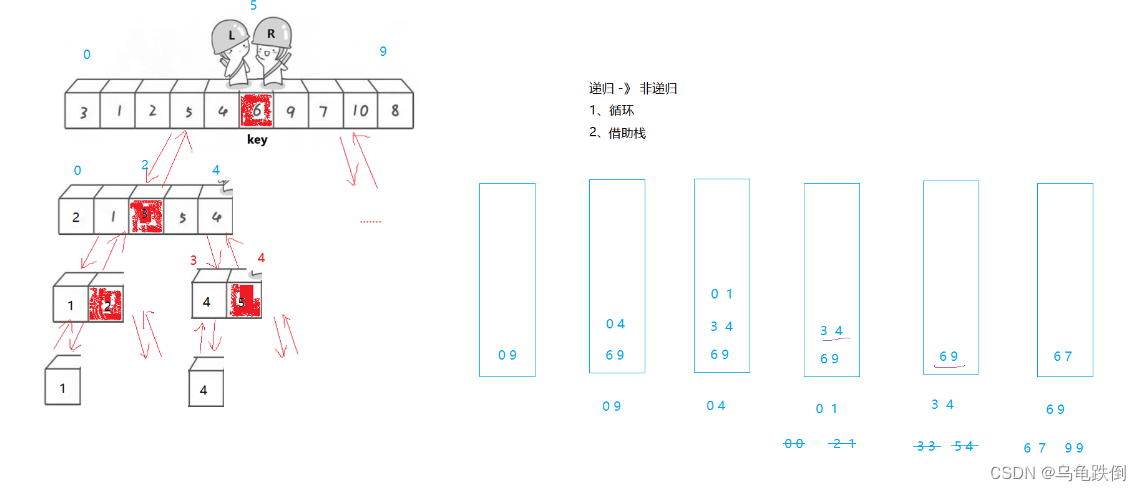
非遞歸快速排序：

遞歸改非遞歸：借助棧
事實上，因為有了三數取中，就可以使得遞歸的深度大大降低，就可以沒有必要再寫一個非遞歸的快排。
但是，我們不能保證，有些時候，遞歸的深度實在是太深了，那么遞歸的方式就行不通，所以，還是要掌握非遞歸
那么，非遞歸要怎么處理呢？
很簡單，用一個棧來處理
因為本質上對于快速排序來說，單趟的邏輯都是一樣的，唯一的區別就是要處理其區間的值
由于，單趟排序的性質，會形成左區間、key、右區間的形式
所以，非常類似于二叉樹的結構，非常適合用遞歸
而遞歸，本質上也是對keyi的值，也就是區間進行處理
例如說，每一個遞歸函數，是建立一個棧幀，在這個函數棧幀里面，單趟邏輯是一樣的
但是，只是從上一層傳進來的數據的區間不一樣
先遞歸左區間，是處理左區間
再遞歸右區間，是處理右區間
一樣的道理
用非遞歸，我們只要控制好這個區間的值就可以了。

所以，使用棧是一個絕佳的方法
首先，begin、end入棧，對這個區間進行單趟處理，返回keyi值
begin、end出棧
再將該keyi的左區間和右區間進棧
再處理棧內記錄的左區間，和有區間
如此循環，直到棧為空，結束排序

所有排序的源碼：

頭文件

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"Stack.h"//插入排序
void InsertSort(int* a, int i);
//希爾排序
void ShellSort(int* a, int n);
//冒泡排序
void BUbbleSort(int *a ,int n);
// 選擇排序
void SelectSort(int* a, int n);
// 堆排序
void AdjustDwon(int* a, int size, int parent);
void HeapSort(int* a, int n);
//快速排序
void QuickSort(int* a,int begin,int end);//非遞歸快速排序
void QuickSortNoneR(int* a, int begin, int end);

實現文件：
?

#include"sort.h"
#include"Stack.h"void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//插入排序
void InsertSort(int* a, int n)
{//[0,end]該區間內是有序，將end+1的數據插入到前面的區間內//再依次往后傳遞//小心越界的問題//數組最后的位置是n-1//我們排序的范圍是，end + 1//要讓end + 1是最后的位置n - 1//那么，最后的范圍要等于n - 2for (int i = 0; i < n - 1; ++i){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}//冒泡排序void BUbbleSort(int* a, int n){for (int i = 0;i<n;++i){for (int  j = 0; j< n - i - 1;++j){if (a[j] > a[j + 1]){Swap(&a[j],&a[j+1]);}}}}//希爾排序
void ShellSort(int* a, int n)
{//預排序//int gap = n;//while (gap > 0)//{//	gap /= 3 + 1;//	for (int i = 0; i < n - gap; i += gap)//	{//		int end = i;//		int tmp = a[end + gap];//		while (end >= 0)//		{//			if (tmp < a[end])//			{//				a[end + gap] = a[end];//				end -= gap;//			}//			else//			{//				break;//			}//		}//		a[end + gap] = tmp;//	}//}int gap = n;while (gap > 1){//這里的gap條件>1,當gap大于1的時候，會進入循環，此時，gap再進行處理，一定會變成1//這就保證了最后一次執行的插入排序一定是gap=1gap = gap / 3 + 1;for (int i = 0; i < n - gap; ++i) {//控制單趟int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}// 選擇排序
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;int maxi = begin;int mini = begin;while (begin < end){for (int i = begin; i < end; ++i){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}Swap(&a[begin], &a[mini]);if (a[mini] > a[maxi]){maxi = mini;}Swap(&a[end], &a[maxi]);}--end;++begin;}}// 堆排序（升序，建大堆）
void AdjustDwon(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size) {if (child + 1 < size  && a[child] < a[child + 1])//保證右孩子存在{child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2+ 1;}else{break;}}}void HeapSort(int* a, int n)
{//向下建堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDwon(a,n,i);}int end = n - 1;while (end > 0){Swap(&a[0],&a[end]);AdjustDwon(a, end, 0);--end;}}int GetMidi(int *a,int  begin, int end)
{int midi = (begin + end) / 2;if (a[begin] > a[end]){if (a[end] > a[midi])return end;else if(a[midi] > a[end])midi;elsereturn begin;}else//a[end] < a[midi]{if (a[end] > a[midi])return end;else if (a[begin] > a[midi])return midi;elsereturn begin;}
}//快速排序：單趟排序-hore版本(增加區間優化)
int PartSort1(int* a, int begin, int end)
{//區間優化if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);int keyi = begin;int left = begin;int right = end;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}//快速排序：單趟排序-挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);int key = a[begin];int left = begin;int right = end;while (left < right){while (left < right && a[right] > key){--right;}Swap(&a[left],&a[right]);while (left < right && a[left] < key){++left;}Swap(&a[left], &a[right]);}a[left] = key;return left;
}//快速排序：單趟排序-前后指針法
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);int keyi = begin;int prev = begin;int cur = prev + 1;初始版本,邏輯上比較好理解//while (cur <= end)//{//	if (a[cur] > a[keyi])//	{//		++cur;//	}//	else//	{//		if (++prev != cur)//		{//			Swap(&a[prev], &a[cur]);//		}//		++cur;//	}//}//簡潔版本while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev],&a[cur]);++cur;}Swap(&a[keyi],&a[prev]);return prev;
}//快速排序
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}//非遞歸實現快速排序
void QuickSortNoneR(int* a, int begin, int end)
{Stack st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);//一定要注意棧的進棧和出棧的規律while (!StackEmpty(&st)){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);int keyi = PartSort3(a, left, right);//[left , keyi - 1] keyi [keyi + 1, right]if(left  < keyi - 1){StackPush(&st, left);StackPush(&st, keyi - 1);}if (keyi + 1 < right){StackPush(&st, keyi + 1);StackPush(&st, right);}}StackDestroy(&st);
}

測試文件：

#include"sort.h"
#include"Stack.h"void printArray(int* a,int n)
{for (int i = 0; i< n;++i){printf("%d ", a[i]);}printf("\n");
}
int a[] = { 9,8,7,6,5,4,3,2,1,0 };void TestInsertSort()
{printf("插入排序：");InsertSort(a, sizeof(a) / sizeof(int));printArray(a, sizeof(a) / sizeof(int));
}void TestBUbbleSort()
{printf("冒泡排序：");BUbbleSort(a, sizeof(a) / sizeof(int));printArray(a, sizeof(a) / sizeof(int));
}void TestshellSort()
{printf("希爾排序：");ShellSort(a, sizeof(a) / sizeof(int));printArray(a, sizeof(a) / sizeof(int));
}void TestHeapSort()
{printf("堆排序：");HeapSort(a, sizeof(a) / sizeof(int));printArray(a, sizeof(a) / sizeof(int));
}void TestSelectSort()
{printf("選擇排序：");HeapSort(a, sizeof(a) / sizeof(int));printArray(a, sizeof(a) / sizeof(int));
}void TestQuickSort()
{printf("快速排序：");QuickSort(a,0, sizeof(a) / sizeof(int) - 1);printArray(a, sizeof(a) / sizeof(int));
}void TestQuickSortNoneR()
{printf("快速排序(非遞歸)：");QuickSortNoneR(a, 0, sizeof(a) / sizeof(int) - 1);printArray(a, sizeof(a) / sizeof(int));
}int main()
{//TestInsertSort();//TestBUbbleSort();//TestshellSort();TestHeapSort();TestSelectSort();//TestQuickSort();//TestQuickSortNoneR();return 0;
}