?Life is a journey, there's no right or wrong.

1. 題目描述

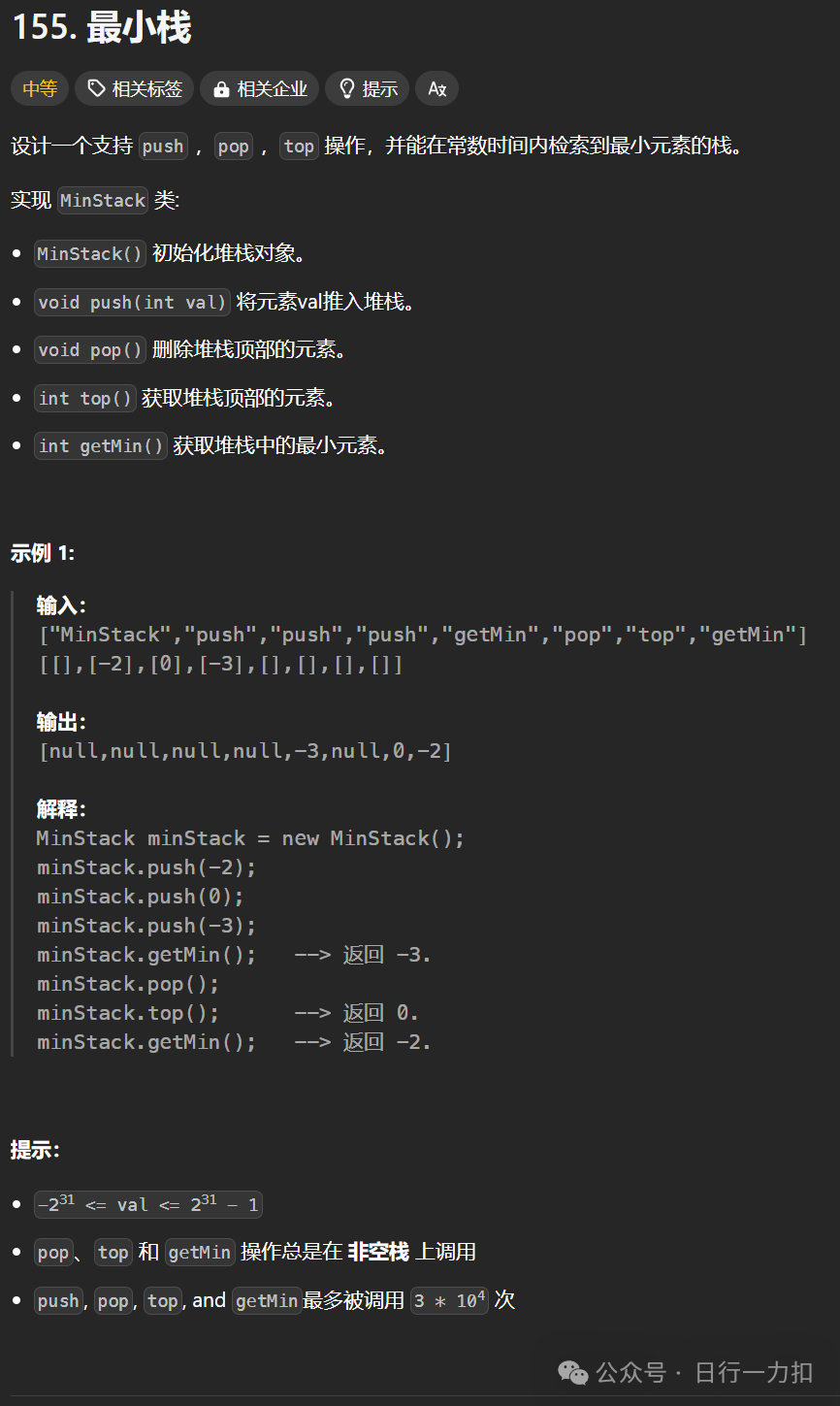
2. ?題目分析與解析

2.1 思路一

看到題目的一瞬間，有沒有注意到 常數時間內檢索到最小元素的棧，那說明我們肯定需要把最小元素的下標存儲起來，這樣才能在常數時間內找到。

其次因為它是一個棧，我們就需要定義一個數組，用來存儲棧內元素。根據棧的 先進后出的性質，需要指定兩個指針，用來指向棧的頭和尾。

代碼思路：

1. 定義一個數組，定義兩個指針表示棧頭尾，定義一個指針表示最小元素的

2. 初始化棧，初始大小及增長自定

3. push操作將元素加入數組，并將尾指針后移1，同時比較當前元素和最小元素大小，取出最小的那個元素的下標更新表示最小元素的的指針

4. pop操作將元素加入數組，并將尾指針前移1，同時比較pop的元素和最小元素大小，如果pop出的元素就是最小元素，那么遍歷數組找到新的最小值存儲在指針

5. top操作取出尾指針指向的元素

6. getMin直接返回最小元素下標的位置的值

7. 注意因為數組長度不能固定，需要在push和pop時動態變化大小

因為題目提示了：

，所以就直接定義數組為int類型。

（不瞞大家，因為兩行代碼的順序問題搞了一上午用python生成了測試用例才找到原因，就在這里記錄一下：

順序問題啊，先拷貝再賦值，我之前先賦值再拷貝）

3. 代碼實現

3.1 思路一

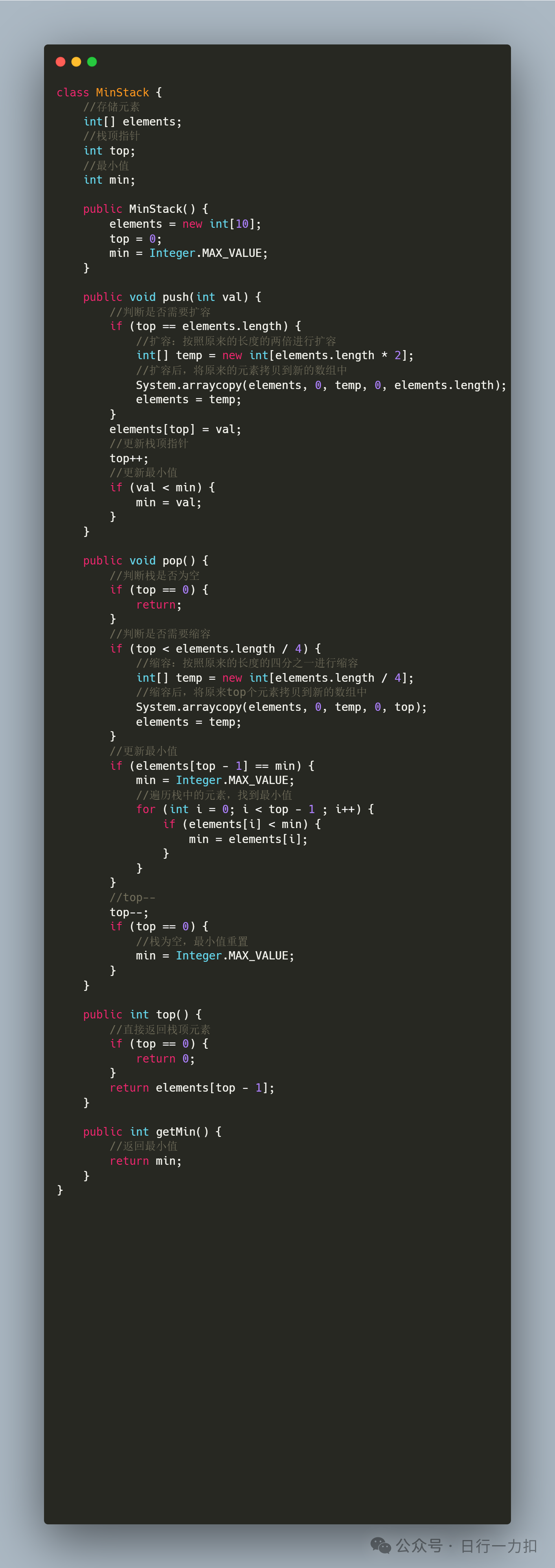
4. 相關復雜度分析

時間復雜度分析：

1. push(int val):

   • 擴容操作的時間復雜度為 O(N)，其中 N 是當前棧中的元素個數。因為在擴容時需要將原數組中的元素拷貝到新數組中。

   • 更新棧頂指針、更新最小值的操作為 O(1)。

2. pop():

   • 縮容操作的時間復雜度為 O(N)，其中 N 是當前棧中的元素個數。因為在縮容時需要將原數組中的元素拷貝到新數組中。

   • 查找新的最小值的操作為 O(N)，其中 N 是當前棧中的元素個數。因為需要遍歷棧中的元素以找到最小值。

   • 更新棧頂指針的操作為 O(1)。

3. top() 和 getMin():

   • 這兩個方法的時間復雜度都為 O(1)，因為它們只是簡單地返回棧頂元素和當前最小值，沒有涉及遍歷或其他復雜操作。

因此，總體來說，push、pop 操作的時間復雜度取決于棧中元素的數量，并且可能會觸發數組擴容和縮容，而這些操作的時間復雜度與元素數量成線性關系。

空間復雜度分析：

1. elements數組的空間復雜度：

   • 最初創建時，數組的長度是 10，因此空間復雜度為 O(1)。

   • 隨著元素的增加、刪除以及數組的擴容和縮容，數組的空間會動態變化，但總體上考慮，空間復雜度為 O(N)，其中 N 是棧中的元素個數。

綜上所述，時間復雜度取決于元素的數量，而空間復雜度隨著元素數量的增加而線性增加。