動態規劃基礎知識
概念
????????動態規劃(Dynamic Programming,DP):用來解決最優化問題的算法思想。
????????動態規劃是分治思想的延伸,通俗一點來說就是大事化小,小事化無的藝術。
????????一般來說,動態規劃將復雜的問題分解為若干子問題,通過綜合子問題的最優解來得到原問題的最優解。
????????動態規劃會將每個求解過的子問題記錄下來,這樣下次碰到相同的子問題,就可以直接使用之前記錄的結果,而不重復計算。
特點
????????最優子結構:動態規劃將一個復雜的問題分解成若干個子問題,通過綜合子問題的最優解來得到原問題的最優解。(“分”與“合”體現在 狀態轉移方程)其實有時候用動態規劃也不一定就是最優解那種意思。
????????重疊子問題:動態規劃會將每個求解過的子問題的解記錄下來,這樣當下一次碰到同樣的子問題時,就可以直接使用之前記錄的結果,而不是重復計算。(雖然動態規劃使用這種方式來提高計算效率,但不能說這種做法就是動態規劃的核心)所謂記錄就是dp數組。
寫法
????????遞歸,自頂向下(Top-down Approach),即從目標問題開始,將它分解成子問題的組合,直到分解至邊界為至。
????????遞推,自底向上(Bottom-up Approach),即從邊界開始,不斷向上解決問題,直到解決了目標問題;
? ? ? ? 適用場景:最大值/最小值, 可不可行, 是不是,方案個數
何時使用動態規劃
????????一個問題必須擁有重疊子問題和最優子結構,才能使用動態規劃去解決。
核心套路:核心就是寫出其狀態轉移方程(窮舉);動態規劃的本質,是對問題 狀態的定義 和 狀態轉移方程的定義 ( 狀態以及狀態之間的遞推關系 )
????????下面給出動態規劃中常用到的一些題目,希望能幫助大家成功掌握這門算法技術,分別為斐波那契類型、矩陣類型、動態規劃在字符串的應用、最長遞增子序列、最長公共子序列、動態規劃在樹種的應用、背包問題等等,如有錯誤,歡迎大家指出,謝謝!
? ? ? ? 創作不易,點波關注再走唄~~~
斐波那契類型
1.1 爬樓梯(簡單70. 爬樓梯)
1.1.1 題目描述
????????假設你正在爬樓梯。需要?n?階你才能到達樓頂。每次你可以爬?1?或?2?個臺階。你有多少種不同的方法可以爬到樓頂呢?
1.1.2 思路
1、動態規劃第一點,先寫出動態規劃的推導公式
? ? ? ? 假設f(x)表示表示爬到第?x級臺階的方案數,考慮最后一步可能跨了一級臺階,也可能跨了兩級臺階,所以可以列舉出以下式子
? ? ? ??
2、探索邊界條件
????????我們是從第 0級開始爬的,所以從第 0級爬到第0級我們可以看作只有一種方案,即 f(0)=1;從第 0級到第1級也只有一種方案,即爬一級,f(1)=1。
1.1.3 復雜度分析
時間復雜度:循環執行 n次,每次花費常數的時間代價,故時間復雜度為 O(n)。
空間復雜度:這里只用了常數個變量作為輔助空間,故空間復雜度為 O(1)。
1.1.4 代碼
#include <iostream>
using namespace std;
class Solution {
public:int climbStairs(int n) {int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
};
int main(){int n = 2;int res = Solution().climbStairs(n);cout << res << endl;
}1.2 斐波那契數(簡單509. 斐波那契數)
1.2.1 題目描述
????????斐波那契數?(通常用?F(n)?表示)形成的序列稱為?斐波那契數列?。該數列由?0?和?1?開始,后面的每一項數字都是前面兩項數字的和。也就是:
- F(0) = 0,F(1)?= 1
- F(n) = F(n - 1) + F(n - 2),其中 n > 1
給定?n?,請計算?F(n)?。
輸入:n=2 輸出:1 ;? 輸入:n=3, 輸出 3
1.2.2 思路
1、推導公式題目已經給出,F(n)=F(n-1)+F(n-2)
2、邊界條件:F(0)和F(1);
3、此題優化的一個方向:使用滾動數組思想將空間復雜度優化成O(1)
1.2.3 復雜度分析
時間復雜度:O(n)
空間復雜度:O(1)
1.2.4 代碼
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:// 簡單509: 斐波那契數int fib(int n) {if (n < 2) {return n;}int p = 0, q = 0, r = 1;for (int i = 2; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
};
int main()
{int n = 3;int res = Solution().fib(n);cout << res << endl;n = 4;res = Solution().fib(n);cout << res << endl;
}1.3 打家劫舍(中等198. 打家劫舍)
1.3.1 題目描述
????????你是一個專業的小偷,計劃偷竊沿街的房屋。每間房內都藏有一定的現金,影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統,如果兩間相鄰的房屋在同一晚上被小偷闖入,系統會自動報警。
????????給定一個代表每個房屋存放金額的非負整數數組,計算你不觸動警報裝置的情況下?,一夜之內能夠偷竊到的最高金額。
1.3.2 思路
這種比較復雜的動態規劃,步驟可能比較麻煩了,可以分為四個解題步驟,如下所示:
- 定義子問題
- 寫出子問題的遞推關系
- 確定DP數組的計算順序
- 空間優化(可選,非必須)
定義子問題
????????原問題為從全部房子,將問題縮小為“從k個房間中能偷到的最大金額”,用f(k)表示;子問題包含參數k。假設共有n個房間,則有n個子問題。動態規劃實際上就是通過求解一堆子問題的解來獲得原問題的解。子問題常需要滿足以下條件:
- 原問題能由子問題表示。
- 一個字問題的解能夠通過其他子問題求解。例如本題中f(k)可以由f(k-1)和f(k-2)求出。
寫出子問題的遞推關系
? ? ? ? 此題中,一共有n個房子,每個房子的金額分別是H0,H1,...,Hn-1,子問題f(k)表示從前k個房子中能偷到的最大金額,那么有兩種偷法。
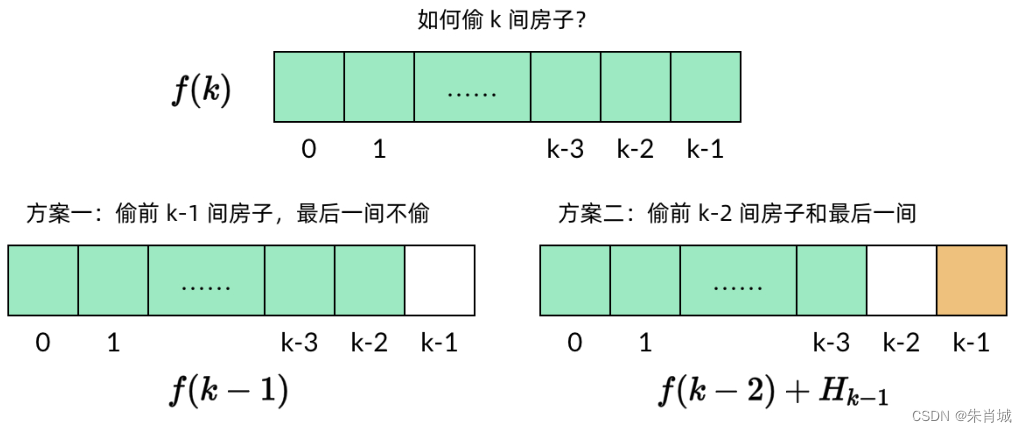
也就是f(k)=max{f(k-1),Hk-1+f(k-2)}; 邊界條件為:f(0)=0,f(1)=H0
確定計算順序
????????在確定了子問題的遞推關系之后,下一步就是依次計算出這些子問題了。在很多教程中都會寫,動態規劃有兩種計算順序,一種是自頂向下的、使用備忘錄的遞歸方法,一種是自底向上的、使用 dp 數組的循環方法。不過在普通的動態規劃題目中,99% 的情況我們都不需要用到備忘錄方法,所以我們最好堅持用自底向上的 dp 數組。
????????DP 數組也可以叫”子問題數組”,因為 DP 數組中的每一個元素都對應一個子問題。如下圖所示,dp[k] 對應子問題 f(k),即偷前k間房子的最大金額。

????????只要搞清楚了子問題的計算順序,就可以確定 DP 數組的計算順序。對于小偷問題,我們分析子問題的依賴關系,發現每個 f(k)依賴 f(k?1)和 f(k?2)。也就是說,dp[k] 依賴 dp[k-1] 和 dp[k-2]。
空間優化
空間優化的基本原理是,很多時候我們并不需要始終持有全部的 DP 數組。對于小偷問題,我們發現,最后一步計算 f(n)f(n)f(n) 的時候,實際上只用到了 f(n?1)f(n-1)f(n?1) 和 f(n?2)f(n-2)f(n?2) 的結果。n?3n-3n?3 之前的子問題,實際上早就已經用不到了。那么,我們可以只用兩個變量保存兩個子問題的結果,就可以依次計算出所有的子問題。
1.3.3 復雜度分析
時間復雜度:O(n)
空間復雜度:O(1)
1.3.4 代碼
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:int rob(vector<int> &nums){int prev = 0;int curr = 0;// 每次循環,計算“偷到當前房子為止的最大金額”for (int i : nums){// 循環開始時,curr 表示 dp[k-1],prev 表示 dp[k-2]// dp[k] = max{ dp[k-1], dp[k-2] + i }int temp = max(curr, prev + i);prev = curr;curr = temp;// 循環結束時,curr 表示 dp[k],prev 表示 dp[k-1]}return curr;}
};
int main()
{vector<int> nums = {1, 2, 3, 1};int res = Solution().rob(nums);cout << res << endl;nums = {2, 7, 9, 3, 1};res = Solution().rob(nums);cout << res << endl;
}斐波那契類型的動態規劃題目練習:
第N個泰波那契數?
刪除并獲得點數
矩陣類型的動態規劃
2.1 中等62. 不同路徑
鏈接:不同路徑
2.1.1 題目描述
一個機器人位于一個?m x n?網格的左上角 (起始點在下圖中標記為 “Start” )。機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角(在下圖中標記為 “Finish” )。問總共有多少條不同的路徑?
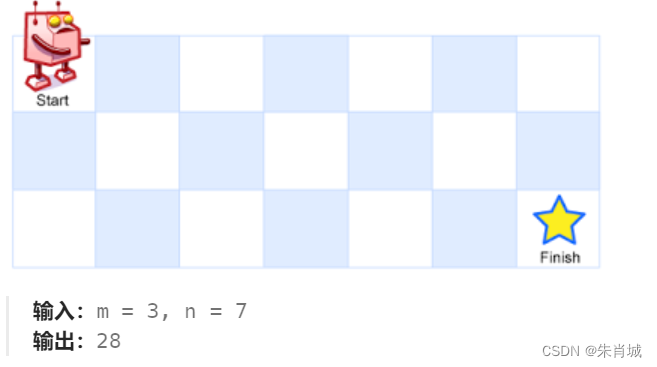
示例2:
輸入:m = 3, n = 2 輸出:3 解釋: 從左上角開始,總共有 3 條路徑可以到達右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
2.1.2 思路
1. 確定dp數組以及下標的含義:dp[i][j] 代表到達矩陣 [i,j] 位置總共具有多少條路徑
2. 確定遞推公式:到達 [i,j] 的路徑總數 dp[i][j] 相當于由 dp[i-1][j]+向下移動一格 和 dp[i][j-1]+向右移動一格 組成。
????????dp[i][j] = dp[i?1][j] + dp[i][j?1];
3. dp數組如何初始化:第0行和第0列都賦值為1
4. 確定遍歷順序:從前到后5. 空間優化:由于dp[i][j]僅與第 i?行和第?i?1 行的狀態有關,因此我們可以使用滾動數組代替代碼中的二維數組,使空間復雜度降低為?O(n)。
2.1.3 復雜度分析
時間復雜度:O(mn)。
空間復雜度:O(min(m,n)),即為存儲所有狀態需要的空間。注意到 f(i,j)僅與第 i行和第 i?1 行的狀態有關,因此我們可以使用滾動數組代替代碼中的二維數組,使空間復雜度降低為 O(n)。此外,由于我們交換行列的值并不會對答案產生影響,因此我們總可以通過交換 m 和 n 使得 m≤n,這樣空間復雜度降低至 O(min?(m,n))。
2.1.4 代碼
class Solution {
public:int uniquePaths(int m, int n){vector<int> f(n, 1);for (int i = 1; i < m; ++i){for (int j = 1; j < n; ++j){f[j] += f[j - 1];}}return f[n - 1];}
};
int main()
{cout << Solution().uniquePaths(3, 7) << endl;cout << Solution().uniquePaths(3, 2) << endl;
}

)





![[linux] matplotlib plt畫training dynamics指標曲線時,標記每個點的值](http://pic.xiahunao.cn/[linux] matplotlib plt畫training dynamics指標曲線時,標記每個點的值)









