目錄

?1 基于Logistic函數的負荷轉移率模型

2 程序示例

3 效果圖

4 下載鏈接

---

負荷需求響應模型種類較多，有電價型和激勵型等類型，本次和大家分享一個基于Logistic函數的負荷轉移率模型，該模型屬于電價型，由于該方法使用的較少，從創新方面給了大家更廣闊的空間。

?1 基于Logistic函數的負荷轉移率模型

由消費者心理學可知，電價差過大、過小以及在電價差變化處響應度曲線平滑性，均會引起用戶需求響應的變化。在電價激勵機制下，用戶本著自愿原則，其響應行為具有明顯的隨機性，則真實需求響應曲線會處于樂觀與悲觀響應預測曲線之間，具備模糊屬性。如圖 2-5 所示，以峰谷負荷轉移為例，建立了基于 Logistic 函數的模糊響應機理，圖中 Δppv 表示峰谷時段電價差，λpv 表示峰轉谷負荷轉移率，即在某時段峰轉谷的負荷量與峰時段平均用電量比值，從而體現用戶對不同電價的響應程度。該模型劃分了“死區”、“響應區”和“飽和區”。在“死區”，由于電價差過小，未能引發用戶自主調整用電模式；在“響應區”，隨著電價差增大，用戶響應積極性被調動；在“飽和區”，雖然電價差很大，但已完全挖掘用戶負荷彈性潛力，因此負荷轉移率值達到極限。另外，當電價差為 0 時，即未采用分時電價，此時用戶響應行為具有很強的隨機性，甚至負荷轉移率出現負值的情況。

基于上述模型，為提高實際情況下分時電價因素對負荷曲線擬合的精度，Logistic 函數利用可變參數，增加負荷轉移率變化的跨度，其函數模型如式?

在式（2-11）中 a 表示函數值范圍，c 為 a/2+b 函數值所對應的橫坐標，近似表示“響應區”電價差的中點，b 用于上下平移函數曲線。基于上述公式，即可提高樂觀和悲觀響應預測曲線的擬合精度，從而反映分時電價對用戶實際響應機理模型的影響。因此，為提高模型精度，本節通過用戶響應隨機性和樂觀響應隸屬度兩個指標對實際用戶響應機理模型進行概率約束。如圖 2-6 所示，在“死區”，電價差過小，用戶響應行為具有很強的隨機性，故由樂觀和悲觀響應預測的平均值確定。在“響應區”，用戶響應行為明顯，且響應行為更傾向于樂觀響應預測曲線。因此需考慮采用偏大型半梯形隸屬度函數計算樂觀響應隸屬度，并將其作為需求響應機理的概率約束。在“飽和區”，由于兩種曲線重合，用戶響應行為即可用負荷轉移率最大值表示。具體計算公式如（2-12）、（2-13）所示。

2 程序示例

程序示例給出峰谷負荷轉移率計算程序，如下所示。

jf=0.8118;%峰段電價jg=0.4438;%谷段電價jp=0.5713;%平段電價dj=[jg.*ones(1,7) jf.*ones(1,7) jg.*ones(1,4) jf.*ones(1,4) jp.*ones(1,2)];%電價情況pload1=[270 225 215 230 245 295 400 425 475 500 560 575 577.5??527.5??450 350 375 450 525 575 600 575 500 425]./20;%負荷detap=jf-jg;%峰谷價差lammax=al/(1+exp(-(detap-cl)/ul))+bl;%樂觀負荷轉移率lammin=ab/(1+exp(-(detap-cb)/ul))+bb;%悲觀負荷轉移率mpv=(jf-jg-apv)/(bpv-apv);%樂觀響應隸屬度detapv=jf-jg;%峰谷價差if detapv<=apv%不同情況下的轉移率lambpv=(lammax+lammin)/2;elseif detapv<=bpvlambpv=lammin+(lammax+lammin)/2*(1+mpv);elselambpv=lammax;end

?程序還需要根據上述編寫平-谷、峰-平的程序段，構成完整程序后可運行得到下面的結果。

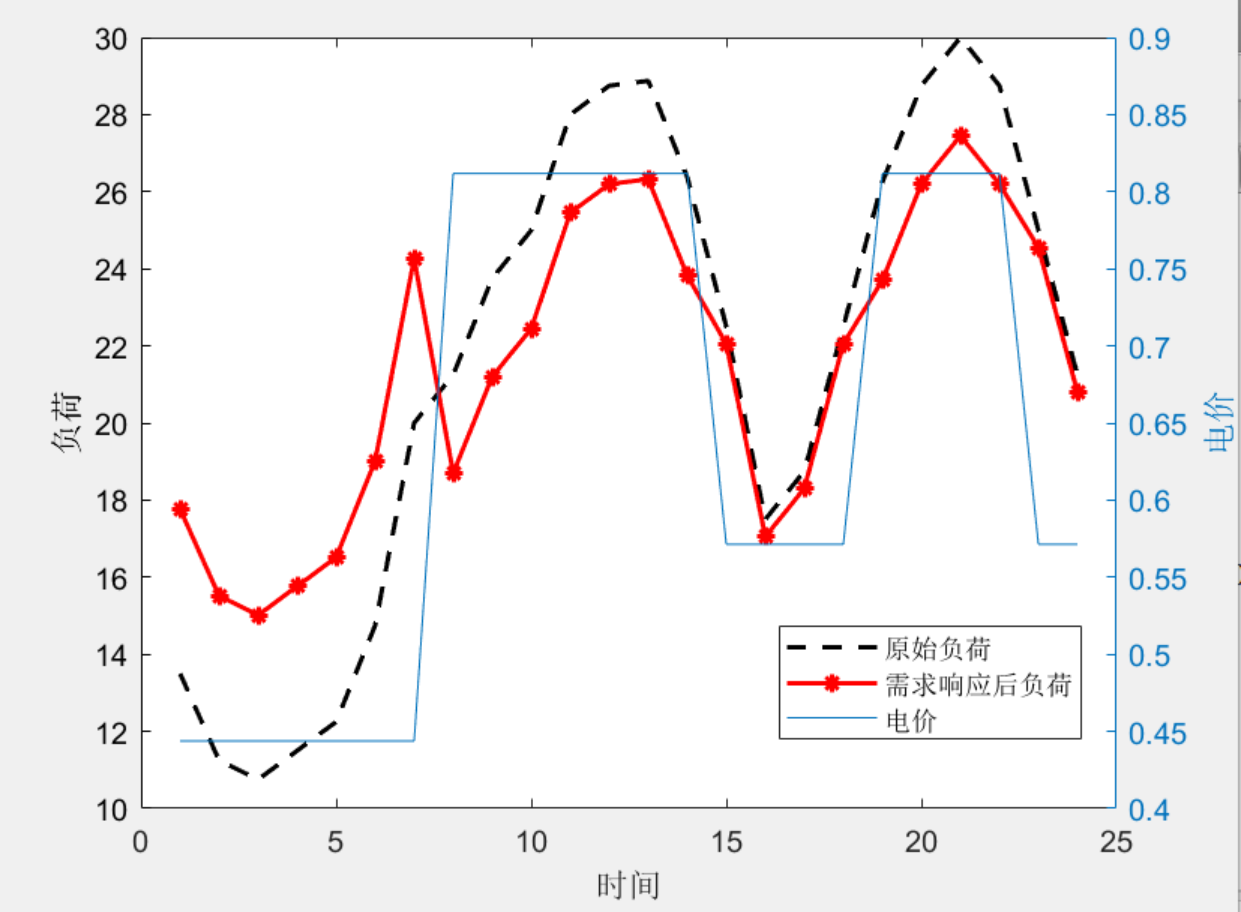
3 效果圖

• 運行程序可以得到如下的效果圖。

4 下載鏈接