所需先驗知識(沒有先驗知識可能會有大礙,了解的話會對D*的理解有幫助):A*算法/ Dijkstra算法
?
何為D*算法
Dijkstra算法是無啟發的尋找圖中兩節點的最短連接路徑的算法,A*算法則是在Dijkstra算法的基礎上加入了啟發函數h(x),以引導Dijkstra算法搜索過程中的搜索方向,讓無必要搜索盡可能的少,從而提升找到最優解速度。這兩者都可應用于機器人的離線路徑規劃問題,即已知環境地圖,已知起點終點,要求尋找一條路徑使機器人能從起點運動到終點。

但是上述兩個算法在實際應用中會出現問題:機器人所擁有的地圖不一定是最新的地圖,或者說,機器人擁有的地圖上明明是可以行走的地方,但是實際運行時卻可能不能走,因為有可能出現有人突然在地上放了個東西,或者桌子被挪動了,或者單純的有一個行人在機人運行時路過或擋在機器人的面前。

碰到這樣的問題,比如機器人沿著預定路徑走到A點時,發現在預先規劃的路徑上,下一個應該走的點被障礙物擋住了,這種情況時,最簡單的想法就是讓機器人停下來,然后重新更新這個障礙物信息,并重新運行一次Dijkstra算法 / A*算法,這樣就能重新找到一條路。
但是這樣子做會帶來一個問題:重復計算。假如如下圖所示新的障礙物僅僅只是擋住了一點點,機器人完全可以小繞一下繞開這個障礙物,然后后面的路徑仍然按照之前規劃的走。可是重復運行Dijkstra算法 / A*算法時卻把后面完全一樣的路徑重新又計算了一遍
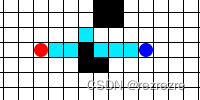
D*算法的存在就是為了解決這個重復計算的問題,在最開始求出目標路徑后,把搜索過程的所有信息保存下來,等后面碰到了先驗未知的障礙物時就可以利用一開始保存下來的信息快速的規劃出新的路徑。
順便一提因為D*算法有上述的特性,所以D*算法可以使用在“無先驗地圖信息/先驗地圖信息不多的環境中的導航”的問題,因為只需要在最開始假裝整個地圖沒有任何障礙,起點到終點的路徑就是一條直線,然后再在在線運行時不斷使用D*算法重新規劃即可。
下面將開始講述D*算法的流程。為此先提及一下算法應用的語境:
機器人已知一個地圖map,在某個起點S,要前往終點E。但是機器人走著走著,突然在中途發現了地圖上沒有標注的障礙物(比如走著走著突然用激光雷達發現前面1米處有一些沒有標注在地圖上的障礙物),而這些障礙物有的擋住了機器人原本規劃好的路,有的沒擋住。
為了簡化,我們認為機器人在柵格地圖上運動,每次運動一個格子(8鄰接),并且機器人為一個點,體積僅占據一個格子大小。
D*算法流程
先說明一下需要用到的類,開始運行前需要對地圖中每個節點創建一個state類對象,以便在搜索中使用。
# 偽代碼
class state:
? ? ? ? # 存儲了每個地圖格子所需的信息,下面會說到這個類用在哪。以下為類成員變量
? ? ? ? x # 橫坐標
? ? ? ? y # 縱坐標
? ? ? ? t = "new" ?# 記錄了當前點是否被搜索過(可為“new”,"open", "close",分別代表這個格子沒被搜索過,這個格子在open表里,這個格子在close表里。關于什么是open表什么是close表,建議去看A*算法,能很快理解)。初始化為new
? ? ? ? parent = None ?# 父指針,指向上一個state,沿著某個點的父指針一路搜索就能找到從這個點到目標點end的最短路徑
? ? ? ? h ?# 當前代價值(D*算法核心)
? ? ? ? k ?# 歷史最小代價值(D*算法核心,意義是所有更新過的h之中最小的h值)
d*算法主代碼:?
function Dstar(map, start, end):
? ? # map:m*n的地圖,記錄了障礙物。map[i][j]是一個state類對象
? ??# start:起點,state類對象
? ? # end: 終點,state類對象
? ??
? ? open_list = [ ] # 新建一個open list用于引導搜索
? ? insert_to_openlist(end,0, open_list) ?# 將終點放入open_list中
? ??
? ? # 第一次搜索,基于離線先驗地圖找到從起點到終點的最短路徑,注意從終點往起點找
? ? loop until (start.t? == “close”):? ? ? ? process_state()? ?# D*算法核心函數之一
? ? end loop
?? ? # 讓機器人一步一步沿著路徑走,有可能在走的過程中會發現新障礙物
? ??
? ? temp_p?= start
? ? while (p != end) do
? ? ? ? if ( unknown obstacle found) then? # 發現新障礙物, 執行重規劃
? ? ? ? ? ? ? ? for new_obstacle in new_obstacles:? ? ?# 對每個新障礙物調用modify_cost函數????
? ? ? ? ? ? ? ? ????????modify_cost( new_obstacle )? #(D*算法核心函數之一)
????????????????end for
? ? ? ? ? ? ? ? do?
???????????????????????? k_min = process_state()
? ? ? ? ? ? ? ? while not ( k_min >= temp_p.h?or open_list.isempty() )? ? ? ? ? ? ? ? continue
? ? ? ? end if
? ? ? ? temp_p = temp_p.parent
? ? ?end while? ??
上述偽代碼中核心函數為2個:modify_cost 和 process_state。我翻閱了csdn幾個關于process_state的解釋,發現都有挺大的錯誤,會讓整個算法在某些情況下陷入死循環(比如D*規劃算法及python實現_mhrobot的博客-CSDN博客)。而且就連原論文的偽代碼都有點問題(可能原論文(Optimal and Effificient Path Planning for Partially-Known Environments,
?function modify_cost( new_obstacle ):
? ? ? ? set_cost(any point to new_obstacle ) = 10000000000? # 讓“從任何點到障礙點的代價”和“從障礙點到任何點的代價” 均設置為無窮大,程序中使用超級大的數代替(考慮8鄰接)
? ? ? ? if new_obstacle.t == "close" then
????????????????insert(new_obstacle, new_obstacle.h )? # 放到open表中,insert也是d*算法中的重要函數之一
? ? ? ? end if
下面是 Process_state函數的偽代碼,注意標紅那條
?function process_state( ):
? ? ? ? ?x = get_min_k_state(oepn_list)? # 拿出openlist中獲取k值最小那個state,這點目的跟A*是一樣的,都是利用k值引導搜索順序,但注意這個k值相當于A*算法中的f值(f=g+h, g為實際代價函數值,h為估計代價啟發函數值),而且在D*中,不使用h這個啟發函數值, 僅使用實際代價值引導搜索,所以其實硬要說,D*更像dijkstra,都是使用實際代價引導搜索而不用啟發函數縮減搜索范圍,D*這點對于后面發現新障礙物進行重新規劃來說是必要的。
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)? # 找到openlist中最小的k值,其實就是上面那個x的k值
? ? ? ? open_list.delete(x)? # 將x從open list中移除, 放入close表
? ? ? ? x.t = "close"? ?# 相當于放入close表,只不過這里不顯式地維護一個close表
? ? ? ??
? ? ? ? # 以下為核心代碼:
? ? ? ? # 第一組判斷
? ? ? ? if k_old < x.h?then? ? ?# 滿足這個條件說明x的h值被修改過,認為x處于raise狀態
? ? ? ? ? ? ? ? for each_neighbor Y of X:? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
? ? ? ? # 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
? ? ? ? ?else:? # 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
????????????????????????if y.t == "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????x.k = x.h? # 注意這行!沒有這行會出現特定情況死循環。在查閱大量資料后,在wikipedia的d*算法頁面中找到解決辦法就是這行代碼。網上大部分資料,包括d*原始論文里都是沒這句的,不知道為啥
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(x, x.h)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t= "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(y,y.h)
????????????????????????????????????????end if
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????????????end if
????????????????end for
????????end if
? ? ? ? return?get_min_k(oepn_list)?
?上面使用到的insert函數:
function insert(state, new_h)? ? ? ?
????if state.t == "new": # 將未探索過的點加入到open表時,h設置為傳進來的 new_hstate.k = h_new # 因為未曾被探索過,k又是歷史最小的h,所以k就是new_helif state.t == "open":state.k = min(state.k, h_new) # 保持k為歷史最小的helif state.t == "close":state.k = min(state.k, h_new) # 保持k為歷史最小的hstate.h = h_new # h意為當前點到終點的代價state.t = "open" # 插入到open表里所以狀態也要維護成openopen_list.add(state) # 插入到open表
以上便是完整的d*算法流程。
D*流程詳解
現在我們從“d*算法主代碼”開始詳解d*函數:
第一次搜索
首先可以看到,在最開始我們需要創建一個open list,然后將終點end加入到open list,之后不斷調用process_state直到起始點start被加入到close表。open表中的東西要按照k值大小排序,每次調用process_state需要取出k值最小的一個來擴展搜索,注意open list中的東西要按照 k 值大小從小到大排序而不是h值。
第一次搜索時,對應主代碼中的:
????# 第一次搜索,基于離線先驗地圖找到從起點到終點的最短路徑,注意從終點往起點找
????loop until (start.t??== “close”):????????process_state()???# D*算法核心函數之一
????end loop?
?這部分。
其實,在首次搜索時,我們可以發現每個點第一次被加入到open表中時都是從new狀態加入,即每次調用insert函數時state.t 最開始都是new,所以其h值與k值其實是相等的;在搜索過程中,也即每一步調用process_state時,k_old 也一直等于x.h(k_old相當于x.k),因此每次第一組判斷都不會被執行,第二組判斷也總是只執行k_old == x.h這部分:
# 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
? ? ? ? ?else:?
? ? ?........
而這部分中,對x的8鄰接點y的判斷只會有兩種情況,①y.t== "new" ?②y.parent != x and y.h >x.h + cost(x,y)。而第三種情況③y.parent == x and y.h !=x.h + cost(x,y) 在這時是不會出現的,因為h的意思是當前點到終點的代價,parent的意思是最短路徑上當前點到終點的路徑的上一個點,那么只要某個點的parent是x,那么這個點的h一定是x的h值加上從x到這個點的代價。第三種情況出現必定是因為y.h、x.h或者cost(x,y)被非正常流程中人為修改過,這在第一次搜索時是不會出現的,而是在重規劃時出現,這點下面一個部分我們再談。
也就是說,在初次搜索時其實整個process_state代碼相當于如下(因為其他部分此時不會被調用):
function process_state****(初次搜索時等價于如下函數)( ):
? ? ? ? ?x = get_min_k_state(oepn_list)?
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)??
? ? ? ? open_list.delete(x)??
? ? ? ? x.t= "close"?
? ? ? ? # 第二組判斷
? ? ? ??for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????? ? ? ? ? ? end if
????? ? end for? ? ? ? ?
? ? ? ? return?get_min_k(oepn_list)?
可以發現,其實這就是dijkstra算法。
實際上,d*算法在初步規劃時,完全退化成了dijkstra算法,也就是說如果沿著規劃出來的路徑運動過程中不發生障礙物變化的話,其實d*效率是要比a*低的,因為d*并沒有啟發式地往目標去搜索,搜索空間實際上比a*大很多。
但是d*這么做主要是為了提高在重規劃時的效率,因為dijkstra算法其實實現的是“找到某個點到空間內所有點的最短路徑”(注意我們是從終點開始往起點搜索的,所以找到的就是全部點到終點的最短路徑)(其實也不是全部點,因為找到起點之后就停止搜索了,沒搜完的都還留在open表中,也就是最短路程大于從起點到終點距離的點都沒被搜。),在運行過程中碰到障礙物需要重規劃時,我們就不再需要從當前點重新搜索到終點,而是找出一條路徑,讓我們繞開障礙物,到達附近沒有障礙物的空閑點即可,而到達這個空閑點之后的路徑不需要重新搜索,因為根據初次搜索,這個空閑點到目的地的最短路徑我們已經有了。
重規劃
接下來我們繼續看主代碼,第一次搜索完之后的部分(該程序默認第一次搜索能找到解,第一次無解的話就沒有重規劃了所以不考慮奧):
# 讓機器人一步一步沿著路徑走,有可能在走的過程中會發現新障礙物
????temp_p?= start
????while (p != end) do
????????if ( unknown obstacle found) then??# 發現新障礙物
????????????????for new_obstacle in new_obstacles:?????# 對每個新障礙物調用modify_cost函數????
????????????????????????modify_cost( new_obstacle )??#(D*算法核心函數之一)
????????????????end for
????????????????do?
?????????????????????????k_min = process_state()
????????????????while not ( k_min >= temp_p.h?or open_list.isempty() )????????????????continue
????????end if
????????temp_p = temp_p.parent
?????end while????
?這里讓temp_p = start然后每一步都讓temp_p = temp_p.partent是為了模擬機器人沿著路徑一步步走的情形。當走到中途通過傳感器發現了新的障礙物時,首先將發現的新障礙物信息加入到已知地圖中,即執行:
for new_obstacle in new_obstacles:?????# 對每個新障礙物調用modify_cost函數????
? ? ? ? modify_cost( new_obstacle )??#(D*算法核心函數之一)
end for
對每個新發現的障礙物點調用 modify_cost(注意,d*無法處理某個點本來是障礙物,現在發現它不再是障礙物的情況,不考慮它,只考慮新增障礙物)
function modify_cost( new_obstacle ):
? ? ? ? set_cost(any point to new_obstacle ) = 10000000000?
? ? ? ? if new_obstacle.t== "close" then
????????????????insert(new_obstacle, new_obstacle.h )? # 放到open表中
? ? ? ? end if
? ? ? ? return
?首先將障礙物到周圍所有點的移動代價設為無窮大。然后,如果
- 新發現的障礙物點狀態是“new”,那就不用管,因為等一下執行process_state時,new點被第一次加入open表中時,這個無窮大的代價就會體現在其周圍的點的h值上。實際上,如果一個點在重規劃時還在new中的話,證明這個點第一次搜索并沒有利用到它的信息,所以它在這次搜索過程中并不算“新成為障礙物”,因為第一次搜索時根本都不知道它是不是障礙物;
- 如果這個點的狀態是“open”,也即這個點在open表中,那么也不用管,因為在open表中等下運行process_state時會被展開,然后其障礙信息會通過cost(x,y)這一項傳遞給周圍的點。(障礙物點本身的h值不是無窮并沒有關系,因為雖然這樣做的話障礙物點本身能找到通往終點的路徑,但是障礙物點本身并不會被機器人占領,所以不用擔心。);
- 如果這個點的狀態是close,那就將其原封不動(也即不用修改其h值)地移入open表,待等下執行process_state時將其障礙信息通過cost傳遞給附近的點即可;
在將新變成障礙物的點放入open表中后(new 的點也總歸會被加入open表,如果沒被加入那證明不需要它),就開始重復執行process_state, 直到找到解或者無解,即這段代碼:
do?
??????????k_min = process_state()
while not ( k_min >= temp_p.h?or open_list.isempty() )
?其中,判斷結束條件的?open_list.isempty() 如果被滿足,即open表為空,意味著無解,這點和A*及dijkstra是一樣的。(當然實際操作時一般不用open表為空作為條件,而是用open表中最小的k值大于等于前面設置的超大的值時就退出,或者在搜索過程中對于那些k值超過前面設置的超大值時,直接不將其加入open表。)
判斷條件的?k_min >= temp_p.h 如果被滿足,則代表找到解(找到從當前點到目標點的新最短路徑)了。簡單來說,?k_min = process_state()這句, process_state()每次都是處理k值最小的點,當open表中最小的k值k_min比當前所在的點的h值還要大的時候,說明當前機器人所在的這個點temp_p已經被搜索過了。
在解釋上面標綠的部分之前,需要提一下h跟k究竟具體代表什么。
h值
在重規劃時,h表示搜到當前這一步的時候,當前這個點到目標點的最小代價,但是它不一定是最終找到最短路徑后的最小代價,因為很可能最短路徑上的點還沒被搜索到呢,等會搜索到比現在這一步還短的路徑時,當前點h的值自然會被修改成沿著那條更短路徑到終點的代價。
k值
對于初次搜索路徑時,k值的意義很明顯就是跟h值是等價的,兩者并無區分,具體意義參考dijkstra和A*算法的實際總代價值。
對于重規劃時,k值意義較為復雜,為了理解它的作用,我們必須看回代碼。因為重規劃實際上也是不斷調用process_state的過程,所以我們去找process_state中所有有可能修改k值的地方(注意下面代碼標紅處):
function process_state( ):
? ? ? ? ?x = get_min_k_state(oepn_list)??
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)??
? ? ? ? open_list.delete(x)??
? ? ? ? x.t= "close"?
? ? ? ??
? ? ? ? # 以下為核心代碼:
? ? ? ? # 第一組判斷
? ? ? ? if k_old < x.h?then?
? ? ? ? ? ? ? ? for each_neighbor Y of X:? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)? # 僅僅只會修改h,不修改k
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
? ? ? ? # 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))? # 調用了insert,可能會涉及k值變化
????????????????????????end if
????????????????end for
? ? ? ? ?else:? # 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
????????????????????????if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))??# 調用了insert,可能會涉及k值變化
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????x.k = x.h?# 直接修改了k!!!!
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(x, x.h)???# 調用了insert,可能會涉及k值變化
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(y,y.h)??# 調用了insert,可能會涉及k值變化
????????????????????????????????????????end if
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????????????end if
????????????????end for
????????end if
? ? ? ? return?get_min_k(oepn_list)?
可以看到稍微涉及到k值變化的也就上面幾個標紅的地方,其中4個都是insert函數。那么我們再來看insert函數:
function insert(state, new_h)???????????????if state.t == "new": ?# 將未探索過的點加入到open表時,h設置為傳進來的 new_h
????????????????state.k = h_new ?# 因為未曾被探索過,k又是歷史最小的h,所以k就是new_h
????????elif state.t == "open":
????????????????state.k = min(state.k, h_new) ?# 保持k為歷史最小的h
????????elif state.t == "close":
? ? ????????????state.k = min(state.k, h_new) ?# 保持k為歷史最小的h
????????state.h = h_new ?# h意為當前點到終點的代價
? ? ? ? state.t = "open" ?# 插入到open表里所以狀態也要維護成open
????????open_list.add(state) ?# 插入到open表
?在insert函數里,一個state的k值僅僅在傳進來的參數new_h比k值更小的時候,k值才會被替換成新h值,這也合理,畢竟原論文中k的意義本身是“歷史h值中最小的h值”嘛。
讓我們再回到重規劃時的process_state這個語境中。想一件事:我有一個地圖,并且我一開始已經知道起點到終點的最短路徑R(也即第一次搜索得到的結果)。可以肯定的是,對于這個最短路徑R上的任何一個點來說,從這個點出發到目的地的最短路徑肯定是前面說的這個最短路徑R的從這個點開始的剩余部分。(反證:因為如果有更短的路,那最短路徑R就不是從起點到終點的最短路徑了呀,我完全可以走到這個點之后走那個更短的路徑,這樣肯定更短,這會出現矛盾)。
現在,我在原來地圖的基礎上額外增加新的障礙物,很可能①障礙物擋在了我原來的最短路徑R上。這種情況下,我可能需要繞一條更長的路才能到達目標,也可能存在一條跟當前路徑一樣長的路,我可以走那條路,但不論怎么說,新的最短路徑長度一定大于等于原本的最短路徑R,絕對不可能比最短路徑R還短(沒理由障礙物多了反而我走的路更短吧)。也可能是②障礙物沒擋住我,那我的最短路徑一定不變。總結來說,發現新障礙物之后的最短路徑一定比原本沒有新障礙物時候的最短路徑長,或者是一樣長。
那么根據上面2段文字,我們知道,加入新障礙物后,某個點到目標點的最短路徑長度,也即代價,一定是只能增不能減的。這說明什么?說明在重規劃這個時候,執行insert函數時傳進來的參數new_h一定不可能比原本的k值小,因為在第一次搜索結束時h跟k是相等的,都是最小代價,加入新障礙物后搜索過程中new_h “新代價”一定要比第一次搜索結束時的h“代價”要大,那也就是肯定比k都大。那也就是說,在重規劃時,insert函數中,k值絕對不可能被更新。
說了3大段那么多,就是想說明一個事情:重規劃時insert函數并不改變k值。那么返回到上面5處標紅代碼,我們可以看到,k值會被改變僅僅只有一個情況。那就是第二組判斷中的某個條件下,直接修改k值那個地方(下面標紅):
function process_state( ):
? ? ? ? ?x = get_min_k_state(oepn_list)??
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)??
? ? ? ? open_list.delete(x)??
? ? ? ? x.t= "close"?
? ? ? ??
? ? ? ? # 以下為核心代碼:
? ? ? ? # 第一組判斷
? ? ? ? if k_old < x.h?then?
? ? ? ? ? ? ? ? for each_neighbor Y of X:? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)? # 僅僅只會修改h,不修改k
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
? ? ? ? # 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))? # 重規劃過程中不修改k
????????????????????????end if
????????????????end for
? ? ? ? ?else:? # 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
????????????????????????if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))??# 重規劃過程中不修改k
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????x.k = x.h?# 唯一一個修改k的地方
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(x, x.h)??# 重規劃過程中不修改k
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(y,y.h)??# 重規劃過程中不修改k
????????????????????????????????????????end if
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????????????end if
????????????????end for
????????end if
? ? ? ? return?get_min_k(oepn_list)?
關于這個標紅的地方的k值究竟會怎么修改,結論是:k值一定會被變大,變得比更新前的k值更大。原因在上面也說過了,在重規劃過程中,所有點的代價一定比原來的大,也即這里出現的所有h值肯定都比第一次搜索結束后的k值大,那x.k=x.h這句,x.h肯定是比x.k大的。
那么什么時候一個點的k值會被修改呢?先告訴你結論:當我們找到了從這個點到目標點的,考慮了新障礙物之后的,新的最短路徑newR后,這個點的k值會標修改成更大,并且這個修改后的k值代表了沿著新的最短路徑newR,這個點到目標點的代價 / 實際距離。注意,如果在新的最短路徑newR上某個點的代價(即到目標的距離)沒有變化,那其k值也不會被改變。至于原因我們將在后面詳解process_state中各判斷條件時討論。
綜上所述,某個點的k值在重規劃時意義如下:
- 如果某個點的k值在重規劃時被修改,那么其修改后的k值就是考慮了新的障礙物之后,這個點到目標點的最短路徑長度(代價)。這里需要注意,被修改k值的點不一定就在機器人接下來要走的路徑上,可能是周圍一大片因為加入了新障礙物導致變化的點,因為重規劃可能不止運行一次,下一次運行重規劃時,地圖是基于此次重規劃之上的,所以需要這一次運行完重規劃后,地圖狀態是維持在dijkstra算法運行完畢,即地圖上每個點都知道自己到目標點的最短路徑的狀態。
- 如果某個點的k值沒被修改,那么其k值就有兩種情況:①一是沒有太大意義,硬要說的話意義就僅僅是“運行重規劃前(即考慮新障礙物前),該點到目標點的最短路徑代價值”;②二是不管考慮新障礙物與否,因為這個點到目標點的最短路徑長度不變,所以其k值沒變。
k的意義如上2種情況,但是其實2情況的①出現的點的數量正常來說是很少的,也就是說我們可以這樣理解:k值的意義基本上就是重規劃后某個點到目標點的最短距離。
那么可能有人會想到,即使2的①情況出現的很少,但是它還是會出現,那這難道不會影響后續又又又發現新障礙物時的重規劃么?答案是不會。原因是因為這部分點其實真的非常少(說實話雖然我不太確定,但是是有可能完全不出現這些點的),而前面也說過,k值真正影響的是搜索的順序,這部分點k值過小僅僅會影響他們在下一次重規劃時優先考察,優先在他們處調用process_state。?并且在調用process_state時就會正常被處理,根據情況決定是否修正其k值,相當于使其回到1.的狀態或者2.②的狀態。如果看到這里不太能理解,那么建議看完下一部分之后再倒回來看看這個地方。
回到前面討論的,結束判斷條件k_min >= temp_p.h代表的意義:
從d*算法主函數中可以看到,重規劃的過程實際上是不斷調用process_state(),直到滿足終止條件為止。每一次調用process_state()都是在從open list(open表)中抽出一個k值最小的state,然后處理它并將其移出open表,然后放入close表或者重新放回open表。也就是說不斷調用process_state的過程中open list中最小的k值k_min的總體趨勢是在不斷增大(oepn list每次都取出一個擁有最小k值的state,并按照條件將新的節點加入open表,這些新節點固然很可能有更小的k使open list中的k_min變小,但是總體趨勢上,k_min是在不斷變大的)。
而對于open表來說,最小的k值k_min表示所有需要搜索的點(即所有在open表中的點),到目標點的距離都大于等于k_min這個值。從上面我們知道temp_p.h代表的意義是當前點(即機器人發現新障礙物時機器人所在的位置)的到目標點的代價(不一定是實際可行的路徑中最小的,但是只要這個值不是無窮大,那證明已經找到從當前點到目標的一條路)。那么,k_min >= temp_p.h這個條件的意義就是“現在還需要繼續搜索的點到目標的距離,已經大于等于現在已經找到的,當前機器人所在點到目標點的距離”,那就是說再搜索下去,即便找到新的路,其代價值也比現在已知的這條路的代價要大,所以不如現在這條路。因此可以說,達到這個條件就可以結束重規劃過程了,因為已經找到最優解了。
詳解process_state
為了真正理解d*算法,必須理解其核心函數process_state。該函數在第一次搜索時意義在上面已經說明,就是完全退化成dijkstgra;?下面對該函數在重規劃過程中的行為進行分析。先再次將這個函數完整地放在這里方便查看:
function process_state( ):
? ? ? ? ?x = get_min_k_state(oepn_list)??
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)??
? ? ? ? open_list.delete(x)??
? ? ? ? x.t= "close"?
? ? ? ??
? ? ? ? # 以下為核心代碼:
? ? ? ? # 第一組判斷
? ? ? ? if k_old < x.h?then?
? ? ? ? ? ? ? ? for each_neighbor Y of X:? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)?
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
? ? ? ? # 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
? ? ? ? ?else:? # 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
????????????????????????if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????x.k = x.h
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(x, x.h)??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(y,y.h)?
????????????????????????????????????????end if
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????????????end if
????????????????end for
????????end if
? ? ? ? return?get_min_k(oepn_list)?
首先先看第一段
? ? ? ? ?x = get_min_k_state(oepn_list)? ? # 從open list中取出k值最小的state
? ? ? ? if x == Null then return -1? ? ? ? # 若沒取到東西證明open_list為空,也就是無解,返回-1
? ? ? ? k_old = get_min_k(oepn_list)? ?# 用一個變量k_old來存這個最小的k值
? ? ? ? open_list.delete(x)? ?# 將x移出open表并放入close表(close表不顯式地維護)
? ? ? ? x.t= "close"? ?# 因為x被放入close表,修改其狀態為close
?這段表明每一次process_state都是取k值最小的一個進行搜索展開,并且被搜索展開的state會被放入close表,這跟a*、dijkstra的本質是一樣的,都是根據一個值引導搜索的先后,在這里這個值是k值。
關于k_old,你沒有看錯,k_old就是等于取出來的x的k值,get_min_k_state 和 get_min_k兩個函數中min k都指的是同一個值。為啥這么寫呢?因為原論文偽代碼就是這樣寫的,那就照抄吧,雖然感覺有點怪怪的。
障礙信息初步傳遞
接下來我們先討論第二組判斷。因為重規劃過程中首先是對新障礙物進行modify_cost操作:
for new_obstacle in new_obstacles:?????# 對每個新障礙物調用modify_cost函數????
? ? ? ? modify_cost( new_obstacle )??#(D*算法核心函數之一)
end for
function modify_cost( new_obstacle ):
? ? ? ? set_cost(any point to new_obstacle ) = 10000000000?
? ? ? ? if new_obstacle.t== "close" then
????????????????insert(new_obstacle, new_obstacle.h )? # 放到open表中
? ? ? ? end if
? ? ? ? return
為了便于理解,假設情況如下,機器人處于下圖的情況
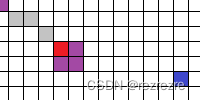
這一步之后所有障礙物點,即紫色點將被原封不動加入open表,即不改變其k值h值,直接放入open表。因為在加入這些障礙物點之前(即第一次搜索之后)open表中最小的k值肯定是大于等于起點的k值的(dijkstra算法特性),所以這些新加入的障礙物點,k值肯定比open表中其他的點的k值都小,那么在調用process_state時一定就是先被搜索。
而當process_state展開這些點時,因為沒有改過其k值h值,所以第一組判斷是不會進入的,而是直接進入第二組判斷的前半k_old == x.h,即會執行下面這段:
if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
?對于每個障礙物點周圍的的點y,如果:
- y是new,也即沒加入過open表的點:那么因為y是第一次被搜素,將y的父節點設置為這個障礙物點,然后將其加入到open表中。注意因為障礙物點到周圍所有點的代價都被設置為無窮大,所以insert這句實際上相當于insert(y,∞), 而y是第一次加入open表,那么其k值也會被設置為無窮。? 在上圖舉例的情況里,只有整個圖左上角那個紫色的點的周圍的點有可能是new,而紅色點附近的紫色點的8鄰接點肯定不是new。如果是因為new而在這一步被把k設置成無窮大,那么這部分點是不會被后續搜索的。但是不用擔心,因為出現這種情況的點是不會影響重新規劃的最短路徑的。
- y不是new(一般來說大部分情況下y都會是close,除非障礙物出現在上次搜索范圍的邊緣才會出現有open的情況,可以想象一下是怎么回事),并且y的父節點是這個新的障礙物點(y.parent == x and y.h !=x.h + cost(x,y) ):注意如果y的父節點是這個新障礙物點,那y.h !=x.h + cost(x,y)一定滿足,因為本來y.h 是等于x.h + cost(x,y)的,但是x變成了障礙物之后cost(x,y)變成了無窮大,右邊就不等于左邊了。(不用管y.h和x.h都是無窮大的情況,這種清情況表示根本沒解,不會被process_state擴展到的)滿足這個條件的y都會被放入open表,但其h值要被設置為無窮大(因為相當于insert(y,∞))
- y不是new,并且y的父節點不是x,而且y當前路徑的代價比“y下一步走到x再走x的最短路徑” 的代價還小,即y.h >x.h + cost(x,y):不可能出現這種情況,因為cost(x,y)是無窮大,不用考慮。所以實際上這時只有上面2種情況
而其他不滿足條件的點,此時也就是y的父節點不是x的點,那么這部分點是不會受到新障礙物影響的,其到終點的最短路徑不會變化,所以不用加入open表重新考察。
對于上面因滿足條件被加入open表的點,發生了什么變化呢?那就是這些點的h值都變成了無窮大,成為了raise狀態!!? ?這個“障礙物點周圍的點h值變為無窮”的過程,就是障礙物信息被傳遞的過程,這個過程還會繼續不斷傳遞下去,但是這次是通過另外的方式,我們馬上就來討論:
障礙信息消除與接力傳遞
在我們將障礙物信息初步傳遞給周圍之后,如果第一次搜索得到的最短路徑并沒有被新發現的障礙物擋住的話,程序到這里就結束了,這也很好理解,我原本的路都沒被擋,那我干嘛要找別的路?就按照原來的肯定就是最短的。但是如果擋住了,這些障礙信息就需要被處理。本來我們討論的目的也是討論如果出問題了會怎么樣嘛,躲不開的:
對于上一步被加入了open表的點,我們知道他們的h值被設置成了無窮,他們處于raise狀態。那么在process_state處理到它們時,這一次會首先從“第一組判斷”開始處理,因為滿足了條件:
# 第一組判斷
? ? ? ? if k_old < x.h?then?
? ? ? ? ? ? ? ? for each_neighbor Y of X:? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)?
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
?這一次x是指在上一步中被加入open表的“障礙物周圍的點”,其h值x.h=無窮大,而k_old是第一次搜索時的值,是一個有限值,代表不考慮障礙物時到目標點的距離。對于x,擴展其8鄰接點并考察每一個點y,如果同時滿足:
- ?y的h值比x的k值小(y.h<k_old):首先只有x周圍的,不是新發現障礙物的點的h值才會不是無窮,而這些點因為還沒被重規劃過程處理過,其h值仍然等于其k值。滿足y.h<k_old 也就意味著,在第一次規劃時,x周圍的,比x更靠近終點的點(這句話需要詳細捋一捋,因為在k_old就是x第一次規劃時的k;y.h又等于y.k,也都是第一次規劃時的值,那在第一次規劃這個語境下,就是y的到終點的代價小于x的代價)。用圖來理解的話,就大概是這個情況:

X標記為點x; 假設終點(藍色)在x的右下方的話,那么粉色為滿足1條件的點; - x當前代價(即無窮大),比x先走y再按y的最短路徑走的代價更大(x.h> y.h + cost(y,x)?):因為x當前代價x.h是無窮大,所以這里的意思就是只要滿足1的幾個點里有不是障礙物的點,那x就從那邊走代價肯定更低。
滿足上面2個條件,也就意味著這個點雖然前往終點的路被新障礙物擋住了,但是我只要小小的拐一下就可以繞開這個障礙物,那么滿足這樣條件的點都會被執行:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)?
也即直接從y那邊繞,也不用再往后搜索了,現在在這步就可以立刻得出到終點最短的路徑。成功被這樣處理的raise狀態的點,h值會因為利用了第一次搜索遺留下來的信息直接下降,這被稱為“初步降低代價”,同時這樣相當于障礙信息被直接消除了。
至于需要大繞的點,比如說需要往后倒退兩步才能繞開障礙物的情況,比如下圖:
?因為往回倒退這個過程會讓代價相對于上一次搜索來說增大,那就設計其他柵格,就需要后續考察了,所以不能在這里直接處理。需要到第二組判斷里處理
第一組判斷結束后,需要進入第二組判斷,如果在第一組判斷中成功修改了x的h值,那么是有可能讓x直接退出raise狀態稱為low狀態的,也即讓x的h值直接變回第一次搜索之后的k值,那么這里在第二組判斷中,就會直接按照dijkstra的思路繼續處理x及其周圍的點了,也即會執行這部分:
if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
因為是dijkstra,所以這部分中的?y.parent == x and y.h !=x.h + cost(x,y)這個條件是不會觸發的,原因可以思考一下。提示一下:x的h值變成了第一次搜索之后的k值,也即k_old。
而如果x沒有直接退出raise狀態,或者x的h值并沒有在第一組判斷中修改,仍然是無窮,那么在這第二組判斷中,就會執行后半部分,并將這個“走另一條路所以路徑邊長了”的信息,或者障礙信息,也即h為正無窮這個信息,傳遞給周圍的鄰格:
else:# 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
????????????????????????if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
? ? ? ? ? ? ? ? ? ? ? ? else?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ?? ? ? ??x.k = x.h
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(x, x.h)??
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? insert(y,y.h)?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????end for
# 為了方便看我又改了改else if 的邏輯,對比一下前面可以知道實際沒有變化哦
?在這部分,也是遍歷x的8鄰接點y,對y有以下情況:
-
y.t== "new" or?(y.parent == x and y.h !=x.h + cost(x,y) ) :y是new表示第一次沒搜索過y;y.parent == x and y.h !=x.h + cost(x,y)表示雖然y父節點指向x但是y的代價不是x的代價加上x到y的代價,這代表y的代價不正確了,它受到了x的變化帶來的影響。這兩種情況直接讓y的父節點指向x, 再insert(y, y下一步走x的話的路徑代價),放到open表里,等會搜索即可。此時如果x的h是無窮,那么相當于x的障礙信息被傳遞給了周圍;如果x.h是有限值,但是比k_old大,那相當于將“x現在要走一條跟之前不一樣長的路”這個信息傳遞給了周圍
-
y.parent != x and y.h >x.h + cost(x,y): y的父節點不是x,但是y的當前路徑長度y.h比“y先走到x再根據x的最短路徑走到終點”的路徑長度 還要長,那說明對y來說,有更短的路!而這個更短的路要經過x,這說明x現在已知的路值得肯定!因為會滿足y.h >x.h + cost(x,y)這個條件時,x.h一定不是正無窮(好像不好說,非常極端的情況下,x.h=∞, y.h=∞+一個值,cost(x,y)=有限值但比前面那個“一個值”小的時候,因為程序中無窮大是用一個非常大的樹數代替的,所以有可能出現這種情況,但是太極端了暫時沒想到怎么構造這種情況,一般應該是不會出現的,先別考慮這個情況出現),那也就是說從x點已經找到新的到達終點的路了,那么現在就讓x的k提升為x的h,這時,x的k值就在新障礙物存在的語境下具有了其應該具有的“最低代價”的意義。*******這也是程序中唯一一個能提升k值的地方,也正因為有這句話,在“發現的新障礙物導致最短路徑會變長”這個情況下,k值,也即實際代價才能正確被提高為更大的值。很多網上的其他資料里,偽代碼里都沒有這句,而且d*原論文里也沒有這句,我認為那是錯誤的,沒有這句話的話,新障礙物擋住路導致新路徑需要變得更長的情況是根本沒辦法處理的,即便第一次重規劃成功,后續很可能又發現新的障礙物,那第二次重規劃時的k值已經完全不再具有在第一次重規劃時k值所具有的的意義了!但是對于一個迭代運行的算法,每一次運行時同樣的變量應該有同樣的意義才對。******
-
(y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old :我們先來討論y.h>k_old這個條件,我們回到第一組判斷里的if中,發現那里有一個“y.h<k_old?”這么樣的條件,很明顯在這里,y.h>k_old就是其互補條件,也就是說我們首先要挑出在第一組判斷中因為“y.h<k_old?”被篩掉的點,考察這些點,那基本上用圖來理解就是這樣:

X標記為點x; 假設終點(藍色)在x的右下方的話,那么粉色為滿足y.h>k_old的點
? ? ? ? 在這部分點中我們再考慮剩下的條件。那么我們再考察y.t = "close" 這個條件。注意到滿足那? ? ? ? ?么一大串條件(y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old)的話需要? ? ? ? ?執行的是insert(y,y.h)?,那如果y.t是“open”的話執行insert又不修改h值的話,相當于什么都沒 ????????干; 如果y.t是“new”的話,就不會到這里了,在第二組判斷的一開始的“if y.t== "new" or ????????xxx那里就執行別的事情去了。
? ? ? ? 那么這里剩下需要討論的條件是y.parent!=x and x.h>y.h+cost(y,x): 這個條件指的是鄰接點y有 ????????不經過x的前往目標點的路徑,并且x按照當前路徑走所需代價比先走到y再沿著y的路徑走的 ????????代價還要大,注意跟2.一樣隱含了y.h不是無窮大,也即y到目標點是有解的這么一個條件。出 ????????現這種情況則將y放入到open表里待重新考察。可是既然x先走y再沿y的路走比按照自己的路? ? ? ? ?走更快,為什么不是修改x的父節點讓其指向y(即讓x.parent = y, x.h = y.h+cost(y,x))呢?因 ????????為其實如果把y加入到open表中,下一次process_state展開這個y的時候,根據y的k和h值的 ????????情況還是會再次考察這里的“y.parent!=x and x.h>y.h+cost(y,x)”這個條件的(相當于展開y這個 ????????點時考察的條件?y.h>x.h+cost(x,y))。
然后我們再來考察上面沒說明的最后一個條件,即第一組判斷中的
if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:?? #考慮8鄰接neighbor
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
上述標紅的條件代表的意義。
先從結論說起,上述條件會被觸發必須滿足前提k_old == x.h, 但是對于那些在重規劃中x.h從頭到尾一直等于k_old的點來說,這里是不會被觸發的,因為對于這樣的點來說相當于新發現的障礙物并不影響其到目標點的路徑代價,所以其h值才一直不變化。只有那些受到新發現障礙物影響,導致x.h先上升了,然后經過后續搜索,修改了x.k的值使得h值與k值又相等了(通過x.k = x.h這一行)的那些點,才有可能會觸發這一段。這代表著x雖然已經找到了到達目標點的新的最短路徑,并且x的k值已經經過修改恢復了正確的意義,但是這個恢復并沒有傳遞到y:y的父節點是x的話,其代價值h應該就等于x.h+cost(x,y)才對,但現在不等,所以需要將其修改正確。之所以要把y再次加入open表,是因為必須把y修改正確之后的信息繼續傳遞給后續的柵格。簡單來說這里的目的就是傳遞修正代價的信息
process_state函數總結
綜上,我們可以得到process_state函數中,達到每個判斷條件時所接受的處理的意義:
function process_state( ):
? ? ? ? ?x = get_min_k_state(oepn_list)??
? ? ? ? if x == Null then return -1
? ? ? ? k_old = get_min_k(oepn_list)??
? ? ? ? open_list.delete(x)??
? ? ? ? x.t= "close"?
? ? ? ??
? ? ? ? # 第一組判斷
? ? ? ? if k_old < x.h?then?
? ? ? ? ? ? ? ? for each_neighbor Y of X:?
? ? ? ? ? ? ? ? ? ? ? ? if y.h<k_old? ?and? x.h> y.h + cost(y,x)? then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? # 嘗試初步降低代價,僅在重規劃時被使用
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.parent = y
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? x.h = y.h + cost(x,y)?
? ? ? ? ? ? ? ? ? ? ? ? end if
? ? ? ? ? ? ? ? end for
? ? ? ? end if?
? ? ? ? # 第二組判斷
? ? ? ? if k_old == x.h then
? ? ? ??????????for each_neighbor Y of X:??
? ? ? ? ? ? ? ? ? ? ? ? if y.t== "new" or? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? # ①dijkstra正常搜素流程
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )? or? ? ?# ②傳遞修正代價的信息
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent != x and y.h >x.h + cost(x,y)) then? ? ?# ③dijkstra正常搜素流程
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?# ②條件僅在重規劃時會被使用,①③在全過程使用
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
????????????????????????end if
????????????????end for
? ? ? ? ?else:? # 不滿足k_old == x.h? 那就是k_old <?x.h
????????????????for each_neighbor Y of X:??
????????????????????????if y.t== "new" or
? ? ? ? ? ? ? ? ? ? ? ? ? ?(y.parent == x and y.h !=x.h + cost(x,y) )?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? # 傳遞路徑代價變化信息(傳遞的可能是障礙信息也可能是“正確路徑產生變化”的信息)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?y.parent = x
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?insert(y, x.h + cost(x,y))
? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?if (y.parent != x and y.h >x.h + cost(x,y))?then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?#?x點已經找到新的到達終點的路了,修正k值使之恢復“最小代價”的含義
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????x.k = x.h
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(x, x.h)??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? else:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? if (y.parent!=x and x.h>y.h+cost(y,x) and y.t = "close" and y.h>k_old then
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????????????# 該點待重新考察,重新放入open表
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????insert(y,y.h)?
????????????????????????????????????????end if
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? end if
????????????????????????end if
????????????????end for
????????end if
? ? ? ? return?get_min_k(oepn_list)?
以上便是關于d*算法,尤其是process_state的詳解。
Python 實踐代碼
以下為實踐代碼,使用時請修改main函數中
NEW_OBS_STEP = 38 # 在走了多少步之后發現新障礙map_png = "./my_map.png" # 初始地圖png圖片obs_png = "./my_map_newobs.png" # 新增障礙物png圖片,要跟初始地圖相同大小,黑色認為是新障礙物?上述3個變量。附帶可用的地圖圖片如下:


(好像只要是圖片就會被CSDN壓,建議自己用畫圖軟件畫2個PNG文件,命名為my_map.png跟my_map_newobs.png,用黑白分別表示障礙物與空閑區域,其中my_map表示最初的地圖,my_map_newobs表示走到一半發現的新障礙物,要求兩個圖片像素長寬一致,推薦都是100*100像素。)
?將2個圖片放到與以下.py文件同目錄并在同目錄下運行以下.py文件即可
但是上面2個圖有csdn加的水印,可能自己畫一張好
#!/usr/bin python
# coding:utf-8
import math
import cv2
from sys import maxsize
NEW_OBS_STEP = 38 # 在走了多少步之后發現新障礙class State(object):def __init__(self, x, y):self.x = xself.y = yself.parent = Noneself.state = "."self.t = "new"self.h = 0self.k = 0def cost(self, state):if self.state == "#" or state.state == "#" or self.state == "%" or state.state == "%":return maxsizereturn math.sqrt(pow(self.x - state.x, 2) + pow(self.y - state.y, 2))def set_state(self, state):# .普通格子 @ 新路徑 # 障礙 % 新障礙 + 第一次搜索的路徑 S 起點 E 終點if state not in [".", "@", "#", "%", "+", "S", "E"]:returnself.state = stateclass Map(object):def __init__(self, row, col):self.row = rowself.col = colself.map = self.init_map()def init_map(self):map_list = []for i in range(self.row):temp = []for j in range(self.col):temp.append(State(i, j))map_list.append(temp)return map_listdef get_neighbors(self, state):state_list = []for i in [-1, 0, 1]:for j in [-1, 0, 1]:if i == 0 and j == 0:continueif state.x + i < 0 or state.x + i >= self.row:continueif state.y + j < 0 or state.y + j >= self.col:continuestate_list.append(self.map[state.x + i][state.y + j])return state_listdef set_obstacle(self, point_list):for i, j in point_list:if i < 0 or i >= self.row or j < 0 or j >= self.col:continueself.map[i][j].set_state("#")class DStar(object):def __init__(self, maps):self.map = mapsself.open_list = set()def process_state(self):x = self.min_state()if x is None:return -1old_k = self.min_k_value()self.remove(x)print("In process_state:(", x.x, ", ", x.y, ", ", x.k, ")")# raise狀態的點,包含兩種情況:①有障礙信息,不知道怎么去終點的點 ②找到了到終點的路徑,但是這條路徑比最初沒障礙的路徑長,還要考察一下if old_k < x.h:for y in self.map.get_neighbors(x):if old_k >= y.h and x.h > y.h + x.cost(y):x.parent = yx.h = y.h + x.cost(y)# low狀態的點if old_k == x.h: # 注意這個開頭的if,不可以是elif,不然算法就不對了。某網上資源是有錯誤的for y in self.map.get_neighbors(x):if ((y.t == "new") or(y.parent == x and y.h != x.h + x.cost(y)) or(y.parent != x and y.h > x.h + x.cost(y))):y.parent = xself.insert_node(y, x.h + x.cost(y))else: # raise狀態的點for y in self.map.get_neighbors(x):if (y.t == "new") or (y.parent == x and y.h != x.h + x.cost(y)):y.parent = xself.insert_node(y, x.h + x.cost(y))else:if y.parent != x and y.h > x.h + x.cost(y):x.k = x.hself.insert_node(x, x.h)else:if y.parent != x and x.h > y.h + x.cost(y) and y.t == "close" and y.h > old_k:self.insert_node(y, y.h)return self.min_k_value()def min_state(self):if not self.open_list:print("Open_list is NULL")return Noneresult = min(self.open_list, key=lambda x: x.k) # 獲取openlist中k值最小對應的節點if result.k >=maxsize/2:return Nonereturn resultdef min_k_value(self):if not self.open_list:return -1result = min([x.k for x in self.open_list]) # 獲取openlist表中值最小的kif result >= maxsize/2:return -1return resultdef insert_node(self, state, h_new):if state.t == "new":state.k = h_newelif state.t == "open":state.k = min(state.k, h_new)elif state.t == "close":state.k = min(state.k, h_new)state.h = h_newstate.t = "open"self.open_list.add(state)def remove(self, state):if state.t == "open":state.t = "close"self.open_list.remove(state)def modify_cost(self, state):if state.t == "close":self.insert_node(state, state.h)def run(self, start, end, obs_pic_path):self.insert_node(end, 0)while True:temp_min_k = self.process_state()if start.t == "close" or temp_min_k == -1:breakstart.set_state("S")s = startwhile s != end:s = s.parentif s is None:print("No route!")returns.set_state("+")s.set_state("E")# 添加噪聲障礙點!!# rand_obs = set()# while len(rand_obs) < 1000:# rand_obs.add((int(random.random()*self.map.row), int(random.random()*self.map.row)))# 根據圖片添加障礙點rand_obs = set()# new_obs_pic = cv2.imread("./my_map_newobs.png")new_obs_pic = cv2.imread(obs_pic_path)for i in range(new_obs_pic.shape[0]):for j in range(new_obs_pic.shape[0]):if new_obs_pic[i][j][0] == 0 and new_obs_pic[i][j][1] == 0 and new_obs_pic[i][j][2] == 0:rand_obs.add((i,j))temp_step = 0 # 當前機器人走了多少步(一步走一格)temp_s = startis_noresult = False # 新障礙物是不是導致了無解while temp_s != end:if temp_step == NEW_OBS_STEP:# 觀察到新障礙for i, j in rand_obs:if self.map.map[i][j].state == "#":continueelse:self.map.map[i][j].set_state("%") # 新增障礙物self.modify_cost(self.map.map[i][j])k_min = self.min_k_value()while not k_min == -1:k_min = self.process_state()if k_min >= temp_s.h or k_min == -1:# 條件之所以是>=x_c.h,是因為如果從x_c找到了到達目的地的路,那么自身的h就會下降,當搜索到k_min比這個h小時,# 證明需要超過“從當前點到終點的最短路徑”的代價的路徑已經找完了,再搜也只會找到更長的路徑,所以沒必要找了,其他# 解都不如這個優。如果一直找不到解,那么x_c.h會是一直是無窮,那么就是說整個openlist都會被搜索完,導致其變為# 空。所以就是無解is_noresult = (k_min == -1)breakif is_noresult:breakif temp_step == NEW_OBS_STEP:draw_s = temp_swhile not draw_s == end:draw_s.set_state("@")draw_s = draw_s.parenttemp_s = temp_s.parenttemp_step +=1temp_s.set_state("E")if __name__ == "__main__":NEW_OBS_STEP = 38 # 在走了多少步之后發現新障礙map_png = "./my_map.png" # 初始地圖png圖片obs_png = "./my_map_newobs.png" # 新增障礙物png圖片,要跟初始地圖相同大小,黑色認為是新障礙物my_map = cv2.imread(map_png)_x_range_max = my_map.shape[0]_y_range_max = my_map.shape[1]mh = Map(_x_range_max,_y_range_max)for i in range(_x_range_max):for j in range(_y_range_max):if my_map[i][j][0] == 0 and my_map[i][j][1] == 0 and my_map[i][j][2] == 0:# png圖片里黑色的點認為是障礙物mh.set_obstacle([[i,j]])start = mh.map[0][0] # 起點為(0,0),左上角end = mh.map[_x_range_max-1][_y_range_max-1] # 終點為(max_x-1,max_y-1),右下角dstar = DStar(mh)dstar.run(start, end, obs_png )for i in range(_x_range_max):for j in range(_y_range_max):if dstar.map.map[i][j].state[0] == "@": # 紅色格子為發現新障礙物重規劃后的路徑my_map[i][j][0] = 0my_map[i][j][1] = 0my_map[i][j][2] = 255elif dstar.map.map[i][j].state[0] == "+": # 藍色格子為第一次搜索的路徑my_map[i][j][0] = 255my_map[i][j][1] = 0my_map[i][j][2] = 0elif dstar.map.map[i][j].state[0] == "%": # 紫色為新發現的障礙物my_map[i][j][0] = 255my_map[i][j][1] = 0my_map[i][j][2] = 255elif dstar.map.map[i][j].state[0] == "E": # 終點my_map[i][j][0] = 128my_map[i][j][1] = 0my_map[i][j][2] = 128cv2.imshow("xx", my_map)cv2.waitKey()cv2.imwrite("./my_map_result.png", my_map)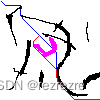
?上圖為運行程序后輸出的結果。
其中左上角為起點,右下角為終點。藍色路徑為第一次規劃的路徑,紫色為走到一半發現的新障礙物,紅色路徑為發現新障礙物后重新規劃的路徑。修改程序中NEW_OBS_STEP變量可以修改走到第幾步發現新的障礙物

![[JavaWeb玩耍日記]HTML+CSS+JS快速使用](http://pic.xiahunao.cn/[JavaWeb玩耍日記]HTML+CSS+JS快速使用)



!)

)
:功能、應用場景和未來發展方向)


)

)
:右側屬性欄(字體、字號、行間距))





