二、數據結構——單鏈表，雙鏈表，棧，隊列，單調棧，單調隊列，KMP，Trie，并查集，堆，哈希表等內容。

? ? ? ? 對于鏈表來說，由于new操作時間太長，因此，算法題中一般使用靜態鏈表。

1.單鏈表

? ? ? ? 采用數組實現單鏈表，可以直接開兩個數據，一個數組存放數值，另外一個數據存放下一個元素（指針）。

示例:實現一個單鏈表，鏈表初始為空，支持三種操作：

向鏈表頭插入一個數；刪除第 k?個插入的數后面的數；
在第 k?個插入的數后插入一個數。
現在要對該鏈表進行 M?次操作，進行完所有操作后，從頭到尾輸出整個鏈表。

注意:題目中第 k?個插入的數并不是指當前鏈表的第 k?個數。例如操作過程中一共插入了 n個數，則按照插入的時間順序，這 n?個數依次為：第 1個插入的數，第 2個插入的數，…第 n?個插入的數。

#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;
int c = 10;int value[N];int ne[N];int head,tal; // tal表示尾部元素在數組中的位置void init(){head = -1;tal = 0;fill_n(&ne[0], sizeof(ne) / sizeof(ne[0]), -1);}void insert_head(int x){value[tal] = x;    // 存放元素ne[tal] = head;    // x指向head指向的元素head = tal++;      // 新的head指向x}void insert_k(int k,int x){ // 在數組第k個位置后插入元素,注意不是鏈表value[tal] = x;         // 存放節點元素ne[tal] = ne[k];        // value[k]指向xne[k] = tal++;          // x指向原value[k]下一個元素}void remove_k(int k){ // 此處沒有釋放空間,算法題一般不必考慮釋放空間int tmp = ne[k];   // 保留刪除前第k個元素的下一個位置ne[k] = ne[ne[k]]; // 第k個元素指向下一個元素的下個元素ne[tmp] = -1;     // 刪除元素的下一個元素位置指向-1}int main(){int m;cin >> m;  // m次操作int k,x;   // k為位置,x為元素char O;    // 操作符init();    // 初始化while(m--){cin >> O;if(O == 'H'){cin >> x; insert_head(x);}  // 頭差一個元素else if(O == 'D')   // 刪除一個元素{cin >> k; if(k == 0) head = ne[head];else remove_k(k-1);}else if(O == 'I'){cin >> k >> x; insert_k(k-1,x);} // 第k個位置插入一個元素}for(int i = head;i!=-1;i=ne[i])printf("%d ",value[i]);return 0;}

?2.雙鏈表

雙鏈表使用兩個數組分別表示前驅和后繼，并用1個數據存儲值。

插入操作：頭插入，需要改頭指針

中間插入，需要防止斷鏈?

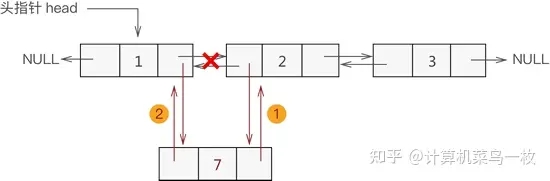
尾部插入需注意改尾指針。

實現一個雙鏈表，雙鏈表初始為空，支持 5種操作：

在最左側插入一個數；
在最右側插入一個數；
將第 k?個插入的數刪除；
在第 k?個插入的數左側插入一個數；
在第 k?個插入的數右側插入一個數
現在要對該鏈表進行 M次操作，進行完所有操作后，從左到右輸出整個鏈表。

注意:題目中第 k個插入的數并不是指當前鏈表的第 k?個數。例如操作過程中一共插入了 n?個數，則按照插入的時間順序，這 n?個數依次為：第 1?個插入的數，第 2?個插入的數，…第 n?個插入的數。

代碼實現：在代碼實現中，左側插入考慮了節點為第一個節點，右側插入考慮了最后一個節點。同時，為了在O(1)時間復雜度完成尾插，設置了表尾指針。

#include <iostream>
#include <algorithm>
using namespace std;const int N = 100010;
int value[N];
int l[N],r[N];
int head,tal,idx; // tal表示尾部元素在數組中的位置void init(){idx = 0;fill_n(&l[0], sizeof(l) / sizeof(l[0]), -1); // 數組初始化為-1fill_n(&r[0], sizeof(r) / sizeof(r[0]), -1);head = -1;tal = -1;}void insert_head(int x){value[idx] = x;    // 存放元素r[idx] = head;  // x指向第一個元素if(tal == -1) tal = idx; // 當前表為空,尾指針指向xelse l[head] = idx;    // 表不為空,第一個元素的前驅指向xhead = idx++;      // 新的head指向x}void insert_tal(int x){value[idx] = x;    // 存放元素l[idx] = tal;      // x的左指針指向最后一個元素if(head == -1) head = idx; // 表位空,頭指針指向xelse r[tal] = idx;  // 表不為空,最后一個元素的后繼指向xtal = idx++;      // 新的tal指向x}void insert_Rk(int k,int x){ // 在數組第k個位置后插入元素,注意不是鏈表value[idx] = x;         // 存放節點元素if(r[k] == -1) {l[idx] = tal; r[idx] = -1; r[tal] = idx;tal = idx++;} // 當前節點為最后一個節點else{l[idx] = k;        r[idx] = r[k];l[r[k]] = idx;r[k] = idx++;  }}void insert_Lk(int k,int x){ // 在數組第k個位置前插入元素,注意不是鏈表value[idx] = x;         // 存放節點元素if(l[k] == -1) {r[idx] = head; l[idx] = -1; l[head] = idx;head = idx++;} // 當前節點在第一個節點else{l[idx] = l[k];r[idx] = k;r[l[k]] = idx;l[k] = idx++;   }}void remove_k(int k){ // 此處沒有釋放空間,算法題一般不必考慮釋放空間if(head == k) head = r[k];if(tal == k) tal = l[k];l[r[k]] = l[k];r[l[k]] = r[k];}int main(){int m;cin >> m;  // m次操作int k,x;   // k為位置,x為元素string O;    // 操作符init();    // 初始化while(m--){cin >> O;if(O == "L"){cin >> x; insert_head(x);}  // 頭差一個元素else if(O == "R"){cin >> x; insert_tal(x);} else if(O == "D")   // 刪除一個元素{cin >> k;remove_k(k-1);}else if(O == "IL"){cin >> k >> x;insert_Lk(k-1,x);} // 第k個位置插入一個元素else{cin >> k >> x; insert_Rk(k-1,x);}}for(int i = head;i!=-1;i=r[i])printf("%d ",value[i]);return 0;}

3.棧

? ? ? ? 棧是先進后出的數據結構，top初始時指向0，代表指向下一個空位置，

  • 入棧時，先入元素，top++，
  • 出棧時，top--；再出元素。
  • top==0判空，top==n-1判滿?
#include <iostream>
#include <algorithm>
using namespace std;const int N = 100010;
int sstack[N],top;void init(){top = 0; // top 指向下一個空位置
}void s_empty(){  // top指向0棧空,否則不空if(top) printf("NO\n");else printf("YES\n");
}void push(int x){  // 入棧,元素先入棧,top++sstack[top++] = x;
}int pop(){   // 出棧:top先減減，再出棧return sstack[--top];
}int query(){  // 查詢棧頂元素int id = top-1;return sstack[id];
}int main(){int m;cin >> m;string op;int x;init();while(m--){cin >> op;if(op=="push") {cin >> x; push(x);}else if(op=="pop") int r = pop();else if(op == "empty") s_empty();else printf("%d\n",query());}
}

應用：表達式求值

算法思想:

使用一個數棧，一個符號棧，從左向右掃描表達式，若：

  • 符號棧為空，直接入棧?
  • 棧頂元素為(，直接入棧
  • 當前符號優先級大于棧頂元素，直接入棧
  • 否則從符號棧中彈出一個符號，并從數棧中彈出2個數字進行運算,直到滿足相應入棧條件
#include <iostream>
#include <algorithm>
#include <stack>
#include <unordered_map>
#include <cstring>
using namespace std;const int N = 100010;
stack<char> op;
stack<int> number;void eval(){    // 實現運算int b = number.top(); // 棧是后進先出,第一個先出的元素是第二個操作數,第二個出的元素是第一個操作數number.pop();int a = number.top();number.pop();char c = op.top();    // 符號op.pop();if(c=='+') number.push(a+b);else if(c=='-') number.push(a-b);else if(c=='*') number.push(a*b);else number.push(a/b);
}int main(){unordered_map <char,int> pr = {{'+',1},{'-',1},{'*',2},{'/',2}};string A; // 表達式cin >> A;int n,j;for(int i=0;i<A.size();i++){n = 0;if(isdigit(A[i])){  // 處理數字j = i;while(isdigit(A[j])) // 數字可能有多位n = 10 * n + (A[j++]-'0'); // 數字是字符形式，轉變為整數number.push(n);i = j-1;}else if(op.empty()) op.push(A[i]); // 符號棧為空,直接入棧else{ if(A[i]=='(') op.push(A[i]); // 棧頂元素為(,直接入棧else if(A[i]==')') {        // 當前符號為),從符號棧中彈出一個符號，并從數棧中彈出2個數字進行運算,直到遇到(while(op.top()!='(')eval();op.pop();  // 彈出(}else if(pr[A[i]]>pr[op.top()]) op.push(A[i]); // 當前符號優先級大于棧頂元素直接入棧else{while(!op.empty() && pr[A[i]]<=pr[op.top()] && op.top()!='(') // 否則從符號棧中彈出一個符號，并從數棧中彈出2個數字進行運算,直到當前符號優先級大于棧頂元素eval();op.push(A[i]); // 當前符號入棧}}}while(!op.empty()) eval(); // 計算剩余部分printf("%d ",number.top());return 0;
}

4.隊列

為了解決假溢出問題，現在隊列一般采用循環隊列，舍棄一個存儲單元

  • 初始化:r=f=0;即r指向隊尾下一個空位置,f指向隊首元素
  • 入隊,先入元素,r=(r+1)%n
  • ?出隊，先出元素，f=(f+1)%n;
  • 判空:r==f;
  • 判滿:(r+1)%n==f;
#include <iostream>
#include <algorithm>
using namespace std;const int N = 100010;
int Queue[N],r,f;void init(){r = f = 0; // r指向下一個空位置,f指向隊首元素
}bool q_empty(){return r == f;
}bool full(){return (r+1) % N == f;
}void en_queue(int x){Queue[r] = x;r = (r+1)%N;
}void de_queue(){f = (f+1)%N;
}int query(){return Queue[f];
}int main(){int m;cin >> m;string op;int x;init();while(m--){cin >> op;if(op=="push") {cin >> x; en_queue(x);}else if(op=="pop") printf("%d\n",de_queue());else if(op == "empty") {if(q_empty()) printf("YES");else printf("NO");}else printf("%d\n",query());}
}

5.單調棧

? ? ? ? 單調棧的應用場景為給定一個長度為 N的整數數列，輸出每個數左邊第一個比它小的數，如果不存在則輸出 ?1。

????????算法分析:如果采用暴力解，則需要2重循環，時間復雜度為O(n^2)。降低時間復雜度可以采用單調棧的方式，即對于元素a[i]，若棧中元素大于a[i]，則退棧，這樣，每個元素進戰出棧1次，時間復雜度為O(n).

#include <iostream>
#include <algorithm>
using namespace std;const int N = 100010;
int s[N];   // 棧
int top =0; // 棧頂指針int main(){int n; // 整數序列長度int x; // 當前數xscanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&x);if(top == 0) {s[top++] =x;printf("-1 ");} // 當前棧為空,輸出結果為-1else{while(s[top-1]>=x) top--;   // 如果棧頂元素大于當前元素,元素出棧if(top == 0) printf("-1 "); // 出棧后棧頂為空，輸出-1else printf("%d ",s[top-1]); // 如果棧不為空,棧頂元素即為所求s[top++] = x;}}}

6.單調隊列

? ? ? ? 單調隊列的應用是找滑動窗口的最大值和最小值，這里的單調隊列可以看做一個兩頭出一頭進的雙端隊列，首先，使用隊列實現滑動窗口，然后在隊尾一側使用棧構建單調隊列，從而找最大值與最小值。

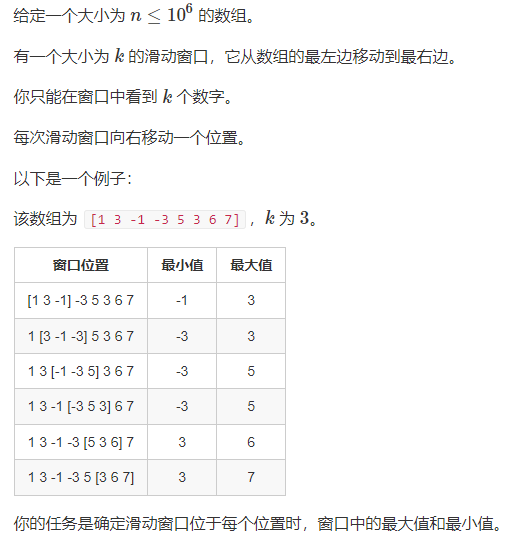
#include <iostream>
#include <algorithm>
using namespace std;
const int N= 1e6+10;
int q[N],a[N];   // q為雙端隊列，存儲數組下標,a為數組
int r,f;        // 隊列首尾指針int main(){int n,k; // n為整數序列長度,k為窗口大小scanf("%d%d",&n,&k); // n為序列長度,k為滑動窗口大小for(int i=0;i<n;i++) scanf("%d",&a[i]);r=f=0;  // 初始化,f指向隊首元素,r指向隊尾元素的下一個空位置for(int i=0;i<n;i++){ // 最小值if(f<r && q[f]<i-k+1) f=(f+1)%N;  // 隊列不空,且隊首元素不在滑動窗口,隊首元素出隊while(a[i]<= a[q[r-1]] && f<r) r=(r-1)%N; // 隊列不空且隊尾元素大于當前元素,隊尾元素出隊q[r]= i;            // 當前元素入隊r= (r+1)%N;         // 隊尾指針++if(i>=k-1) printf("%d ",a[q[f]]); // i=k-1為第一個窗口,開始輸出元素}printf("\n");r=f=0;for(int i=0;i<n;i++){ // 最大值if(f<r && q[f]<i-k+1) f=(f+1)%N;while(a[i]>= a[q[r-1]] && f<r) r=(r-1)%N;q[r]= i;r= (r+1)%N;if(i>=k-1) printf("%d ",a[q[f]]);}return 0;
}

7.kmp算法

????????kmp算法是利用子串的性質降低暴力解的時間復雜度。利用子串的最長公共前后綴使每次前綴的位置移動到后綴的位置。

?

最后next數組為最長公共前后綴的長度+1?

#include <iostream>
#include <algorithm>
using namespace std;const int N = 1e5+10;
const int M = 1e6+10;
char p[N],s[M];
int ne[N];int main(){int n,m;cin >> n;cin >> p+1;cin >> m;cin >> s+1;int i,j;for(i=2,j=0;i<=n;i++){ // 構建next數組while(j && p[i]!=p[j+1]) j = ne[j]; // 當前不匹配,子串移動,while循環主要用于解決多個子串匹配的情形if(p[i]==p[j+1]) j++;  // 當前匹配,繼續匹配ne[i] = j;        // 構建當前元素的next值}//for(i=0;i<n;i++) printf("%d ",ne[i]);//printf("\n");for(i=1,j=0;i<=m;i++){while(j && s[i]!=p[j+1]) j = ne[j];if(s[i]==p[j+1]) j++;if(j==n){   // 子串匹配成功printf("%d ",i-n); // 輸出下標從0開始j = ne[j];  // 繼續匹配下一個子串}}return 0;
}

8.trile樹

? ? ? ? ?trile最重要的作用為高效的存儲字符串,并能夠很好的統計字符串出現的次數。其結構如下：

實例:

維護一個字符串集合，支持兩種操作：

  1. I x?向集合中插入一個字符串?x；
  2. Q x?詢問一個字符串在集合中出現了多少次。

共有?N 個操作，所有輸入的字符串總長度不超過?105105，字符串僅包含小寫英文字母。

#include <iostream>using namespace std;const int N = 1e5+10;
int son[N][26]; // 存儲子節點行號
int cnt[N];     // 字符串出現次數,注意，這是以字符串最后字符的創建為id
int idx = 0;    // 創建節點的id
char str[N];    // 創建節點void insert_t(char str[]){int p = 0;int u;for(int i=0;str[i];i++){u = str[i] - 'a'; // 字符索引if(!son[p][u]) son[p][u] = ++idx; // 無節點,創建節點,值為創建時的id,可通過此id索引字符串,子節點也為對應的行p = son[p][u];   // 有子節點,進入子節點}cnt[p]++;  // 字符串出現次數+1
}int query(char str[]){int p = 0;int u;for(int i=0;str[i];i++){u = str[i] - 'a';  // 字符索引if(!son[p][u]) return 0; // 檢索到了空節點,說明此節點p = son[p][u];   // 有子節點,進入子節點}return cnt[p]; // 返回出現次數
}int main(){int n;scanf("%d",&n);while(n--){char op[2];scanf("%s%s",op,str);if(op[0]=='I') insert_t(str);else printf("%d\n",query(str));}return 0;
}

應用:最大異或對

在給定的 N 個整數 A1，A2 ......An 中選出兩個進行 or (異或)運算，得到的結果最大是多少?

????????算法思想:如果采用暴力解，則需要2重循環，時間復雜度為O(N^2)。分析異或運算過程，從最高位開始， 相同結果為0，不同結果為1，因此，我們可以以各位數字建立一顆二叉樹，從而簡化查找長度，查找某個數的最大異或的數時，從高位開始，盡量進入具有不同數的分支中

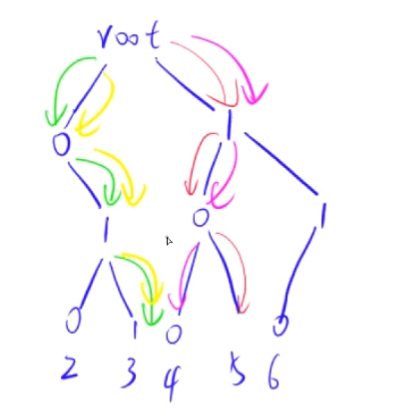
#include <iostream>using namespace std;const int N = 1e7+10;
int son[N][2];
int a[N];
int idx = 0;void insert_t(int x){int p = 0;int s;for(int i=30;i>=0;i--){ // 創建trile樹s = x >> i & 1; // 右移i位或1,即判斷第i位是0還是1if(!son[p][s]) son[p][s] = ++idx; // 以創建節點的id作為子節點索引p = son[p][s]; // 進入子節點}
}int query(int x){int p = 0;int s;int res = 0;for(int i=30;i>=0;i--){s = x >> i & 1; // 右移i位或1,即判斷第i位是0還是1if(son[p][!s]) {res += 1 << i;p = son[p][!s];} // 異或運算,該位不同結果最大,進入該位不同的分支else p = son[p][s]; // 所有數該位相同,進入子樹}return res;
}int main(){int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);insert_t(a[i]);}int res = 0;for(int i=0;i<n;i++){ res = max(res,query(a[i]));}printf("%d",res);return 0;
}

9.并查集

作用：在近似于O(1)的時間復雜度內完成以下2種操作：
1.將兩個集合合并
2. 詢問兩個元素是否在一個集合當中
基本原理: 每個集合用一棵樹來表示。樹根的編號就是整個集合的編號。每個節點存儲
它的父節點，p[x]表示x的父節點
問題1:如何判斷樹根: if (p[x] == x)
問題2:如何求x的集合編號: while (p[x] != x) x = p[x];優化:路徑壓縮

問題3:如何合并兩個集合: px 是x的集合編號，py是y的集合編號。p[x] = y

一共有?n?個數，編號是?1～n，最開始每個數各自在一個集合中。

現在要進行?m個操作，操作共有兩種：

  1. M a b，將編號為?a和?b的兩個數所在的集合合并，如果兩個數已經在同一個集合中，則忽略這個操作；
  2. Q a b，詢問編號為?a和?b的兩個數是否在同一個集合中；
#include <iostream>
using namespace std;const int N = 1e5+10;
int p[N];   // 父節點數組int find(int x){if(p[x]!=x) p[x] = find(p[x]);  // 路徑壓縮,x的父節點指向根return p[x];
}int main(){int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i] = i; // 初始化,每個節點指向自己的集合char op[2];int a,b;while(m--){scanf("%s%d%d",op,&a,&b);if(op[0]=='M') p[find(a)] = find(b); // 合并,a集合的根指向belse{if(find(a)==find(b)) printf("Yes\n"); // 同一集合else printf("No\n");}}return 0;
}

變體：?

給定一個包含 n 個點(編號為 1~ n)的無向圖，初始時圖中沒有邊
現在要進行 m個操作，操作共有三種
1. c a b ，在點a和點6之間連 條邊，a和6可能相等
2. Q1 a b ，詢問點 a 和點6 是否在同一個連通塊中，a 和6可能相等
3.Q2 a ，詢問點 a 所在連通塊中點的數量?

????????分析：此處需要求連通塊中點的數量，因此需要額外維護一個信息，即每個集合元素的個數（只有根節點有意義）。

#include <iostream>
using namespace std;const int N = 1e5+10;
int p[N];   // 父節點
int s[N];   // 存儲集合中元素的數量,只有根節點有意義int find(int x){if(p[x]!=x) p[x] = find(p[x]);return p[x];
}int main(){int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) {p[i] = i;s[i] = 1;}char op[5];int a,b;while(m--){scanf("%s",op);if(op[0]=='C') {   scanf("%d%d",&a,&b);if(find(a)==find(b)) continue;s[find(b)] += s[find(a)];  // 集合節點數目增加p[find(a)] = find(b);}else if(op[1]=='1'){scanf("%d%d",&a,&b);if(find(a)==find(b)) printf("Yes\n");else printf("No\n");}else{scanf("%d",&a);printf("%d\n",s[find(a)]);}}return 0;
}

食物鏈問題

動物王國中有三類動物 4,B,C，這三類動物的食物鏈構成了有趣的環形。A吃B，B吃C，C吃A.
現有個動物，以1~ N 編號每個動物都是 A,B,C中的一種，但是我們并不知道它到底是哪一種。
有人用兩種說法對這 N個動物所構成的食物鏈關系進行描述:
第一種說法是 1XY，表示X和Y是同類
第二種說法是 2 XY，表示X吃Y
此人對 N 個動物，用上述兩種說法，一句接一句地說出 K 句話，這 K 句話有的是真的，有的是假的
當一句話滿足下列三條之一時，這句話就是假話，否則就是真話.
1.當前的話與前面的某些真的話沖突，就是假話
2.當前的話中 X或Y比N大，就是假話:
3.當前的話表示 X 吃 X，就是假話.
你的任務是根據給定的 N 和 K 句話，輸出假話的總數?

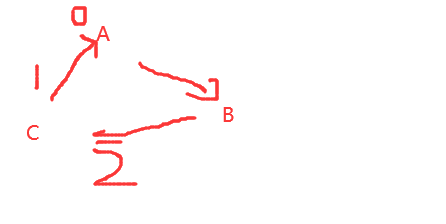
算法思想：該問題為3個種群的關系問題，可以采用并查集處理。額外維護一個距離根節點的深度信息，若d[find(x)]-d[find(y)]模3為0，表明是同類。若d[find(x)]-d[find(y)]模3為1，則表明x是y的天敵。代碼如下：

10.堆

如何手寫一個堆?

1. 插入一個數? ? ? ? ? ? ? ?heap[ ++ size] = x; up(size);? 插到末尾,自下向上調整堆
2.求集合當中的最小值? heap[1];（小根堆）
3. 刪除最小值? ? ? ? ? ? ? ? heap[1] = heap[size]; szie -- ; down(1);
4.刪除任意一個元素? ? ??heap[k] = heap[size]; size -- ; down(k); up(k)
5.修改任意一個元素? ? ? heap[k] = x; down(k); up(k);

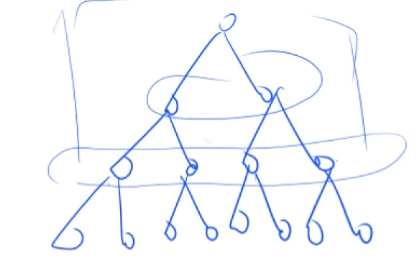
輸入一個長度為 n 的整數數列，從小到大輸出前 m 小的數

#include <iostream>
#include <algorithm>
using namespace std;const int N = 1e5+10;
int heap[N],hsize; // hsize表示堆的大小void down(int i){  // 元素下沉操作int t;while(2*i <= hsize){  // 節點i(從1開始),其做孩子為2i,右孩子為2i+1,t = 2 * i;if(2*i+1 <= hsize && heap[2*i+1] < heap[2*i]) t++;  // 孩子中的較小者比根小,則交換//printf("%d ",heap[t]);if(heap[t]<heap[i]) {swap(heap[t],heap[i]);i = t;}  else break;}
}int main(){int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&heap[i]);hsize = n;for(int i=n/2;i>0;i--) down(i); // 從n/2開始下沉,表示從第n-1開始下沉,可實現在O(n)時間復雜度建堆while(m--){printf("%d ",heap[1]);swap(heap[1],heap[hsize]); // 將堆首元素輸出hsize--;down(1); // 向下調整堆}return 0;
}

維護一個集合，初始時集合為空，支持如下幾種操作
1.I x，插入一個數2;
2.PM ，輸出當前集合中的最小值
3.DM，刪除當前集合中的最小值 (數據保證此時的最小值唯一)
4.DK，刪除第k個插入的數;
5.C?k x ，修改第k個插入的數，將其變為 a
現在要進行N次操作，對于所有第 2 個操作，輸出當前集合的最小值?

#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;const int N = 1e5+10;
int heap[N],hp[N],ph[N],hsize; // ph[k]將插入的第k個元素對應到堆的索引j;hp[j]將堆中數組下標為i對應到第k個插入元素void h_swap(int a,int b){   // 不僅需要交換堆元素,還需要維護額外的信息swap(ph[hp[a]],ph[hp[b]]); // 交換元素在堆中的索引swap(heap[a],heap[b]);  // 交換元素swap(hp[a],hp[b]);      // 交換堆索引對應插入元素的順序
}void down(int i){  // 自上而下調整堆int t;while(2*i <= hsize){t = 2 * i;if(2*i+1 <= hsize && heap[2*i+1] < heap[2*i]) t++;//printf("%d ",heap[t]);if(heap[t]<heap[i]) {h_swap(t,i);i = t;}else break;}
}void up(int i){   // 自下而上調整堆while(i/2 && heap[i/2]>heap[i]){h_swap(i/2,i);i = i/2;}
}int main(){int n;scanf("%d",&n);char op[5];int k,x;int c=0;    // 計數while(n--){scanf("%s",op);if(!strcmp(op,"I")){hsize++,c++;  // 索引++,堆大小++scanf("%d",&heap[hsize]);hp[hsize] =  c;  // 堆中數組下標為i對應到第k個插入元素ph[c] = hsize;   // 插入的第k個元素對應到堆的索引jup(hsize);   // 插入元素,自上而下調整堆}else if(!strcmp(op,"PM")) printf("%d\n",heap[1]); // 輸出堆首元素else if(!strcmp(op,"DM")) { // 輸出堆首元素h_swap(1,hsize);  // 交換堆首和堆尾元素hsize--;down(1);         // 自上而下調整堆}else if(!strcmp(op,"D")){scanf("%d",&k);  // 刪除第k個插入的元素k = ph[k];    // 第k個插入的元素對應堆的索引h_swap(k,hsize); // 交換該元素和堆尾元素hsize--;down(k);up(k);  // 實際只會執行一種調整,為了書寫方便}else{  // 更改第k個插入元素的值scanf("%d%d",&k,&x);k = ph[k];  // 第k個插入的元素對應堆的索引 heap[k] = x; // 更改值down(k);up(k); // 實際只會執行一種調整,為了書寫方便}}return 0;
}

11.哈希表

????????哈希表是一種高效的數據結構，它通過哈希函數將鍵映射到存儲位置，從而實現快速的插入、刪除和查找操作，理想情況下時間復雜度為O(1)。然而，在實際應用中可能會遇到沖突，即不同的鍵映射到同一位置。為解決這些沖突，哈希表采用了鏈地址法、開放地址法等方法。

實例：此處采用鏈地址法解決沖突

維護一個集合，支持如下幾種操作
1.I x ，插入一個整數a;
2.Q x ，詢問整數 是否在集合中出現過
現在要進行 N 次操作，對于每個詢問操作輸出對應的結果?

#include <iostream>using namespace std;
const int N = 1e5+7;typedef struct Node
{int data;Node* next;};Node* H[N];void insert(int x){Node* node = new Node();node->data = x;node->next = NULL;int k = (x % N + N)%N; // 哈希函數映射位置,此處處理了負值的情況Node* p = H[k];if(!p) H[k] = node;  // 表位置為空,直接插入else{       // 位置不空,插入到表頭node->next = p->next;p->next = node;}
}void find(int x){int k = (x % N + N)%N;Node* p = H[k];while (p) // 表位置不空,進入查找{   if(p->data == x) break;p = p->next;}if(!p) printf("No\n");else printf("Yes\n");
}int main(){char op[5]; // 運算符int x;  // 值int m; // m次操作scanf("%d",&m);while (m--){scanf("%s%d",op,&x);if(op[0]=='I') insert(x);else find(x);}return 0;
}

字符串哈希

（1）字符串哈希值的表示

? ? ? ? 將字符串哈希用p進制的數表示。例如：“ABCD”的值用H=ASCII(A)*p^3+ASCII(B)*p^2+ASCII(C)*p^1+ASCII(D)*p^0，然后字符串的哈希值為H%Q，其中當p=131或13331，Q=2^64時，不會發生沖突，此時unsigned long long類型的表示即為對應的哈希值。

（2）用處

? ? ? ? 可以在O(1)的時間復雜度內求出[l,r]區間子串的哈希值。

12.STL庫

在C++中，vector是一個動態數組，其大小可以在運行時更改。初始化vector的方式有多種，這取決于你想如何初始化它。以下是一些示例：

  1. 默認初始化???????

std::vector<int> vec;

這將創建一個沒有任何元素的空vector。
2.?使用給定的大小初始化

std::vector<int> vec(10); // 創建一個大小為10的vector，所有元素默認初始化為0（對于int類型）

3.使用給定的大小和值初始化

std::vector<int> vec(10, 5); // 創建一個大小為10的vector，所有元素初始化為5

4.使用初始化列表初始化

std::vector<int> vec = {1, 2, 3, 4, 5}; // 創建一個包含5個元素的vector

5.通過復制另一個vector初始化

std::vector<int> vec1 = {1, 2, 3, 4, 5};
std::vector<int> vec2(vec1); // 創建一個與vec1相同的vector

在C++中，std::vector?提供了大量的成員函數來支持各種操作，包括訪問元素、修改元素、管理大小和容量等。以下是一些常用的?std::vector?成員函數：

訪問元素

  • at(size_type pos): 訪問指定位置的元素，并進行邊界檢查。
  • operator[]: 通過索引訪問元素，不進行邊界檢查（更快，但使用時要小心）。
  • front(): 訪問第一個元素。
  • back(): 訪問最后一個元素。

修改元素

  • push_back(const T& value): 在末尾添加一個元素。
  • pop_back(): 移除末尾的元素。
  • insert(iterator pos, const T& value): 在指定位置插入一個元素。
  • erase(iterator pos): 移除指定位置的元素。
  • erase(iterator first, iterator last): 移除一系列元素。
  • swap(vector& other): 交換兩個向量的內容。
  • clear(): 清除所有元素。
  • emplace(const_iterator pos, args): 在指定位置構造并插入一個元素（C++11起）。
  • emplace_back(args): 在末尾構造并添加一個元素（C++11起）。

大小和容量

  • size(): 返回元素的數量。
  • empty(): 檢查是否為空。
  • capacity(): 返回當前已分配的空間能容納的元素數量。
  • resize(size_type n): 改變大小。
  • reserve(size_type n): 預留空間。
  • shrink_to_fit(): 請求移除未使用的容量（C++11起，非綁定性）。

其他

  • assign(size_type n, const T& value): 替換所有元素。
  • begin(): 返回指向第一個元素的迭代器。
  • end(): 返回指向最后一個元素之后位置的迭代器。
  • cbegin(),?cend(): 返回常量迭代器（C++11起）。
  • rbegin(),?rend(): 返回反向迭代器。
  • crbegin(),?crend(): 返回常量反向迭代器（C++11起）。
  • emplace_iterator,?begin(size_type),?end(size_type): （C++20起）用于支持結構化綁定的新接口。

vector, 變長數組，倍增的思想
? ? size() ?返回元素個數
? ? empty() ?返回是否為空
? ? clear() ?清空
? ? front()/back()
? ? push_back()/pop_back()
? ? begin()/end()
? ? []
? ? 支持比較運算，按字典序

pair<int, int>
? ? first, 第一個元素
? ? second, 第二個元素
? ? 支持比較運算，以first為第一關鍵字，以second為第二關鍵字（字典序）

string，字符串
? ? size()/length() ?返回字符串長度
? ? empty()
? ? clear()
? ? substr(起始下標，(子串長度)) ?返回子串
? ? c_str() ?返回字符串所在字符數組的起始地址

queue, 隊列
? ? size()
? ? empty()
? ? push() ?向隊尾插入一個元素
? ? front() ?返回隊頭元素
? ? back() ?返回隊尾元素
? ? pop() ?彈出隊頭元素

priority_queue, 優先隊列，默認是大根堆
? ? size()
? ? empty()
? ? push() ?插入一個元素
? ? top() ?返回堆頂元素
? ? pop() ?彈出堆頂元素
? ? 定義成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;

stack, 棧
? ? size()
? ? empty()
? ? push() ?向棧頂插入一個元素
? ? top() ?返回棧頂元素
? ? pop() ?彈出棧頂元素

deque, 雙端隊列
? ? size()
? ? empty()
? ? clear()
? ? front()/back()
? ? push_back()/pop_back()
? ? push_front()/pop_front()
? ? begin()/end()
? ? []

set, map, multiset, multimap, 基于平衡二叉樹（紅黑樹），動態維護有序序列
? ? size()
? ? empty()
? ? clear()
? ? begin()/end()
? ? ++, -- 返回前驅和后繼，時間復雜度 O(logn)

? ? set/multiset
? ? ? ? insert() ?插入一個數
? ? ? ? find() ?查找一個數
? ? ? ? count() ?返回某一個數的個數
? ? ? ? erase()
? ? ? ? ? ? (1) 輸入是一個數x，刪除所有x ? O(k + logn)
? ? ? ? ? ? (2) 輸入一個迭代器，刪除這個迭代器
? ? ? ? lower_bound()/upper_bound()
? ? ? ? ? ? lower_bound(x) ?返回大于等于x的最小的數的迭代器
? ? ? ? ? ? upper_bound(x) ?返回大于x的最小的數的迭代器
? ? map/multimap
? ? ? ? insert() ?插入的數是一個pair
? ? ? ? erase() ?輸入的參數是pair或者迭代器
? ? ? ? find()
? ? ? ? [] ?注意multimap不支持此操作。 時間復雜度是 O(logn)
? ? ? ? lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
? ? 和上面類似，增刪改查的時間復雜度是 O(1)
? ? 不支持 lower_bound()/upper_bound()， 迭代器的++，--

bitset, 圧位
? ? bitset<10000> s;
? ? ~, &, |, ^
? ? >>, <<
? ? ==, !=
? ? []

? ? count() ?返回有多少個1

? ? any() ?判斷是否至少有一個1
? ? none() ?判斷是否全為0

? ? set() ?把所有位置成1
? ? set(k, v) ?將第k位變成v
? ? reset() ?把所有位變成0
? ? flip() ?等價于~
? ? flip(k) 把第k位取反

參考：常用代碼模板2——數據結構 - AcWing

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/718065.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/718065.shtml
英文地址，請注明出處：http://en.pswp.cn/news/718065.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

JavaScript“基本語法”筆記（自學第一天）！

JavaScript“基本語法”筆記（自學第一天）！

一、JavaScript的用途和應用領域 JavaScript的應用領域非常廣泛&#xff0c;主要包括以下幾個方面&#xff1a; 網頁交互性: JavaScript最初是為了增強網頁的交互性而開發的&#xff0c;它可以控制網頁的行為、樣式和內容&#xff0c;使用戶能夠與網頁進行實時交互&#xff0c…
閱讀更多...
一個教材上的CMS網站源碼在Linux服務器上登錄時驗證碼正常，但在windows下不能正常顯示

一個教材上的CMS網站源碼在Linux服務器上登錄時驗證碼正常，但在windows下不能正常顯示

一個教材上的CMS網站源碼在Linux服務器上登錄時驗證碼正常&#xff0c;但在windows下不能正常顯示。 在linux服務器上能正常顯示。顯示界面如下所示&#xff1a;
閱讀更多...
蜻蜓FM語音下載（mediadown）

蜻蜓FM語音下載（mediadown）

一、介紹 蜻蜓FM語音下載&#xff08;mediadown&#xff09;&#xff0c;能夠幫助你下載蜻蜓FM音頻節目。如果你是蜻蜓FM會員&#xff0c;它還能幫你下載會員節目。 二、下載地址 本站下載&#xff1a;蜻蜓FM語音下載&#xff08;mediadown&#xff09; 百度網盤下載&#…
閱讀更多...
Web 應用防火墻（WAF）：功能、應用場景和未來發展方向

Web 應用防火墻（WAF）：功能、應用場景和未來發展方向

Web 應用防火墻&#xff08;WAF&#xff09;是一種用于保護 Web 應用程序免受各種網絡攻擊的安全工具。WAF 可以檢測并阻止對 Web 應用程序的惡意攻擊&#xff0c;如SQL 注入、跨站腳本&#xff08;XSS&#xff09;和跨站請求偽造&#xff08;CSRF&#xff09;等。它通過檢查 H…
閱讀更多...
【Redis 主從復制】

【Redis 主從復制】

文章目錄 1 :peach:環境配置:peach:1.1 :apple:三種配置方式:apple:1.2 :apple:驗證:apple:1.3 :apple:斷開復制和切主:apple:1.4 :apple:安全性:apple:1.5 :apple:只讀:apple:1.6 :apple:傳輸延遲:apple: 2 :peach:拓撲結構:peach:2.1 :apple:?主?從結構:apple:2.2 :apple:?…
閱讀更多...
【MetaGPT】配置教程

【MetaGPT】配置教程

MetaGPT配置教程&#xff08;使用智譜AI的GLM-4&#xff09; 文章目錄 MetaGPT配置教程&#xff08;使用智譜AI的GLM-4&#xff09;零、為什么要學MetaGPT一、配置環境二、克隆代碼倉庫三、設置智譜AI配置四、 示例demo&#xff08;狼羊對決&#xff09;五、參考鏈接 零、為什么…
閱讀更多...
大數據技術（一）

大數據技術（一）

大數據技術概述 大數據技術層面及其功能 數據采集與預處理 利用ETL(extract-transform-load)工具將分布的、異構數據源中的數據&#xff0c;如關系數據、平面數據文件等&#xff0c;抽取到臨時中間層后進行清洗、轉換、集成&#xff0c;最后加載到數據倉庫或數據集市中&…
閱讀更多...
C語言什么是循環嵌套？

C語言什么是循環嵌套？

一、問題 分?結構是可以進?嵌套的&#xff0c;循環結構同樣也?持嵌套&#xff0c;那什么是循環嵌套呢&#xff1f; 二、解答 ?個循環體內?包含另?個完整的循環結構&#xff0c;就稱之為循環嵌套。內嵌的循環中還可以嵌套循環&#xff0c;這就是多層循環&#xff0c;也叫…
閱讀更多...
類與對象詳解 C++ （1）

類與對象詳解 C++ （1）

1.struct和class 與C語言不同的是&#xff0c;C中struct和class可以定義成員變量和成員函數。更偏好用class。 2.類的定義 格式如下&#xff1a; class 為 定義類的 關鍵字&#xff0c; ClassName 為類的名字&#xff0c; {} 中為類的主體&#xff0c;注意 類定義結束時后面…
閱讀更多...
前端canvas項目實戰——簡歷制作網站(五)：右側屬性欄(字體、字號、行間距)

前端canvas項目實戰——簡歷制作網站(五)：右側屬性欄(字體、字號、行間距)

目錄 前言一、效果展示二、實現步驟1. 優化代碼&#xff0c;提取常量2. 實現3個編輯模塊3. 實現updateFontProperty方法4. 一個常見的用法&#xff1a;僅更新當前選中文字的樣式 三、Show u the code后記 前言 上一篇博文中&#xff0c;我們擴充了線條對象&#xff08;fabric.…
閱讀更多...
springboot 整合oauth2

springboot 整合oauth2

1、EnableOAuth2Client&#xff1a;客戶端&#xff0c;提供OAuth2RestTemplate&#xff0c;用于客戶端訪問資源服務。 簡要步驟&#xff1a;客戶端訪問資源->客戶端發現沒有資源訪問token->客戶端根據授權類型生成跳轉url->瀏覽器 302 到認證授權服務進行認證、授權。…
閱讀更多...
Dockerfile構建過程詳解

Dockerfile構建過程詳解

Dockerfile介紹 docker是用來構建docker鏡像的文件&#xff01;命令參數腳本&#xff01; 構建步驟&#xff1a; 1、編寫一個dockerfile文件 2、docker build構建成為一個鏡像 3、docker run 運行鏡像 …
閱讀更多...
PDF轉Excel的未來：人工智能技術如何提升轉換效率和準確性

PDF轉Excel的未來：人工智能技術如何提升轉換效率和準確性

隨著信息技術的快速發展&#xff0c;PDF和Excel作為兩種重要的文件格式&#xff0c;在日常生活和工作中扮演著至關重要的角色。PDF以其獨特的跨平臺閱讀特性&#xff0c;成為了文件分享和傳輸的首選格式&#xff1b;而Excel則以其強大的數據處理能力&#xff0c;成為了數據分析…
閱讀更多...
【二分查找】【C++算法】378. 有序矩陣中第 K 小的元素

【二分查找】【C++算法】378. 有序矩陣中第 K 小的元素

作者推薦 視頻算法專題 本文涉及的基礎知識點 二分查找算法合集 LeetCode378. 有序矩陣中第 K 小的元素 給你一個 n x n 矩陣 matrix &#xff0c;其中每行和每列元素均按升序排序&#xff0c;找到矩陣中第 k 小的元素。 請注意&#xff0c;它是 排序后 的第 k 小元素&…
閱讀更多...
機器人持續學習基準LIBERO系列10——文件結構

機器人持續學習基準LIBERO系列10——文件結構

0.前置 機器人持續學習基準LIBERO系列1——基本介紹與安裝測試機器人持續學習基準LIBERO系列2——路徑與基準基本信息機器人持續學習基準LIBERO系列3——相機畫面可視化及單步移動更新機器人持續學習基準LIBERO系列4——robosuite最基本demo機器人持續學習基準LIBERO系列5——…
閱讀更多...
力扣日記3.3-【回溯算法篇】332. 重新安排行程

力扣日記3.3-【回溯算法篇】332. 重新安排行程

力扣日記&#xff1a;【回溯算法篇】332. 重新安排行程 日期&#xff1a;2023.3.3 參考&#xff1a;代碼隨想錄、力扣 ps&#xff1a;因為是困難題&#xff0c;望而卻步了一星期。。。T^T 332. 重新安排行程 題目描述 難度&#xff1a;困難 給你一份航線列表 tickets &#xf…
閱讀更多...
牛客小白月賽86

牛客小白月賽86

A-水鹽平衡_牛客小白月賽86 (nowcoder.com) #include<bits/stdc.h> #define endl \n #define int long long using namespace std; int a,b,c,d; void solve() {cin>>a>>b>>c>>d;if((double)a/b>(double)c/d) cout<<S<<endl;els…
閱讀更多...
關于脈沖負載應用中電阻器，您需要了解的 11 件事？

關于脈沖負載應用中電阻器，您需要了解的 11 件事？

不幸的是&#xff0c;電阻器在脈沖負載下可能會失效。當脈沖功率耗散到器件的電阻元件時&#xff0c;它會產生熱量并增加電阻器的溫度。過熱會損壞電阻元件&#xff0c;導致電阻變化甚至設備開路。為了避免在設計中出現這種情況&#xff0c;以下是您在選擇元件時應了解的有關電…
閱讀更多...
excel統計分析——拉丁方設計

excel統計分析——拉丁方設計

參考資料&#xff1a;生物統計學 拉丁方設計也是隨機區組設計&#xff0c;是對隨機區組設計的一種改進。它在行的方向和列的方向都可以看成區組&#xff0c;因此能實現雙向誤差的控制。在一般的試驗設計中&#xff0c;拉丁方常被看作雙區組設計&#xff0c;用于提高發現處理效應…
閱讀更多...
Skipped breakpoint at because it happened inside debugger evaluation親測可用

Skipped breakpoint at because it happened inside debugger evaluation親測可用

問題描述&#xff1a; 在多線程項目中&#xff0c;在idea中打斷點時&#xff0c;有時會遇到下面這種情況&#xff1a; idea左下角出現一行紅底或者綠底文字提示&#xff1a; Skipped breakpoint at because it happened inside debugger evaluation 然后我們能感受到的就是…
閱讀更多...
最新文章

Copyright @ 2022~2023