本篇文章參考：比較易懂的 Manacher（馬拉車）算法配圖詳解

馬拉車算法可以求出一個字符串中的最長回文子串，時間復雜度 $O(n)$

因為字符串長度的奇偶性，回文子串的中心可能是一個字符，也可能是兩個字符中間的位置，所以為了解決這個問題，我們在每兩個字符之間加一個 # ，開頭再加一個 $ 防止越界

比如說：

abcd 變成 $#a#b#c#d#

接下來是后文需要的一些定義：

• c 表示當前已經計算過的最靠右的回文子串的中心點的下標
• m 表示以 c 為中心的回文子串的右端點下標
• p[i] 表示以 s[i] 為中心的回文子串的半徑（包括自身）

對于以每一個位置為中心點的時候單獨計算，復雜度很大，馬拉車可以對其進行很好地優化

目前的難點就是怎么計算 p[i]

看上面這張圖，我們當前需要計算 p[i]，我們可以去找 i 關于 c 的對稱點（記為 j），因為我們是從左往右計算的，所以 p[j] 已經計算過了，如果以 j 為中心的回文子串在以 c 為中心的回文子串中時，我們可以直接把 p[j] 賦給 p[i]

當然會出現一些特殊情況：

• 如果 p[j] + i > m，如下圖所示，以 c 為中心的回文子串包不住，我們就更新 p[i] = m - i （先只更新確定的部分）
  
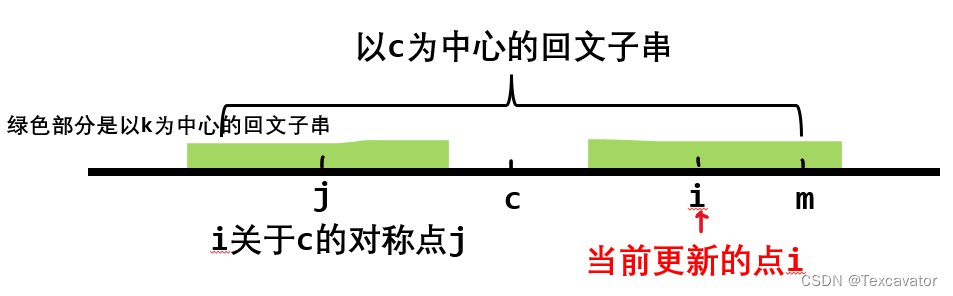
• 如果 i 在 m 右側，如下圖所示，更新 p[i] = 1
  

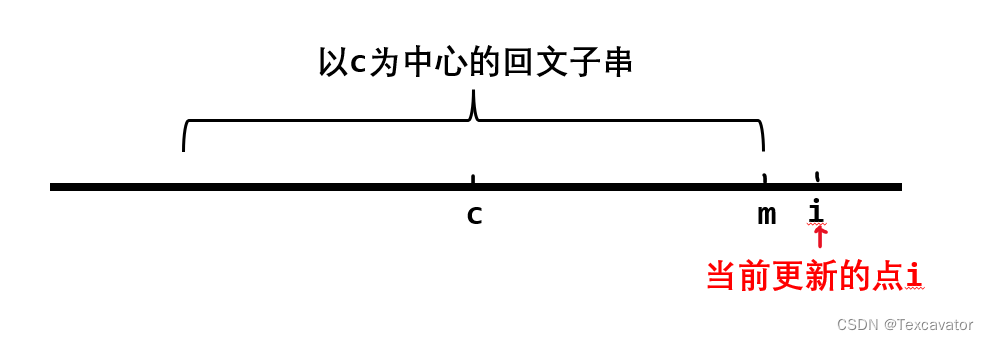
上面的情況都只能得到半成品的 p[i]，所以需要對 s[i] 進行中心擴展，得到最終的 p[i]

如果最終的 p[i] + i > m 此時已經有比以 c 為中心的回文子串更靠右的回文子串了，就把 c = i m = p[i] + 1

求完 p[i] 后算法結束

求最長回文子串板子

string Manacher(string s)
{int sl = s.size(); // 原字符串長度if (sl == 0 || sl == 1) return s;// 構建新串string ns = "$#";for (int i = 0; i < sl; i ++ ){ns += s[i];ns += '#';}int len = ns.size();int c = 0; // 最靠右的回文子串的中心點下標int m = 0; // 最靠右的回文子串的右端點下標int pos = 0; // 最長回文子串的中心點int maxlen = 0; // 最長回文子串的半徑（不包括中心點）（新字符串中）vector<int> p(len); // p[i]表示以i為中心點的回文子串的半徑（包括i）for (int i = 1; i < len; i ++ ){if (i < m) p[i] = min(p[c - (i - c)], m - i + 1); // c-(i-c)是i關于c的對稱點 當前情況表示i在目前最靠右側的回文子串中else p[i] = 1 + (ns[i] != '#'); // 當前不是#的話 其兩側就是# 所以半徑可以加1if (i - p[i] >= 0 && i + p[i] < ns.size())while (ns[i - p[i]] == ns[i + p[i]]) p[i] ++ ; // 對半成品的i位置進行中心擴散if (i + p[i] - 1 > m) // 產生了比以c為中心時更靠右的回文子串{c = i;m = i + p[i] - 1;}if (p[i] - 1 > maxlen) // 更新最長回文子串{maxlen = p[i] - 1;pos = i;}}string ans = "";char tmp;for (int i = 0; i < 2 * maxlen * 1; i ++ ) // 遍歷最長字串的每個位置 得出原字符串中的最長字串{tmp = ns[pos - (maxlen - 1) + i];if (tmp != '#') ans += tmp;}return ans;
}

求最長前綴or后綴回文子串板子

string Manacher(string s)
{int sl = s.size(); // 原字符串長度if (sl == 0 || sl == 1) return s;// 構建新串string ns = "$#";for (int i = 0; i < sl; i ++ ){ns += s[i];ns += '#';}int len = ns.size();int c = 0; // 最靠右的回文子串的中心點下標int m = 0; // 最靠右的回文子串的右端點下標int pos = 0; // 最長回文子串的中心點int maxlen = 0; // 最長回文子串的半徑（不包括中心點）（新字符串中）// int flag; // 可以用這個標記是前綴回文子串最長還是后綴回文子串最長vector<int> p(len); // p[i]表示以i為中心點的回文子串的半徑（包括i）for (int i = 1; i < len; i ++ ){if (i < m) p[i] = min(p[c - (i - c)], m - i + 1); // c-(i-c)是i關于c的對稱點 當前情況表示i在目前最靠右側的回文子串中else p[i] = 1 + (ns[i] != '#'); // 當前不是#的話 其兩側就是# 所以半徑可以加1if (i - p[i] >= 0 && i + p[i] < ns.size())while (ns[i - p[i]] == ns[i + p[i]]) p[i] ++ ; // 對半成品的i位置進行中心擴散if (i + p[i] - 1 > m) // 產生了比以c為中心時更靠右的回文子串{c = i;m = i + p[i] - 1;}if (p[i] == i && maxlen < p[i]) // 最長前綴回文子串{maxlen = p[i] - 1;pos = i;// flag = 1;}if (p[i] + i == len && maxlen < p[i]) // 最長后綴回文子串{maxlen = p[i] - 1;pos = i;// flag = 2;}}string ans = "";char tmp;for (int i = 0; i < 2 * maxlen * 1; i ++ ) // 遍歷最長字串的每個位置 得出原字符串中的最長字串{tmp = ns[pos - (maxlen - 1) + i];if (tmp != '#') ans += tmp;}return ans;
}