? ? ? ? ?經歷了2023年的秋招,現在也已經入職半年了,空閑時間將面試中可能遇到的機器學習問題整理了一下,可能答案也會有錯誤的,希望大家能指出!另外,不論是實習,還是校招,都祝福大家能夠拿到滿意的Offer!
機器學習面經系列的其他部分如下所示:
機器學習-面經(part2)-交叉驗證、超參數優化、評價指標等內容
機器學習-面經(part3)-正則化、特征工程面試問題與解答合集
機器學習-面經(part4)-決策樹共5000字的面試問題與解答
1、機器學習模型
1.1 有監督學習模型
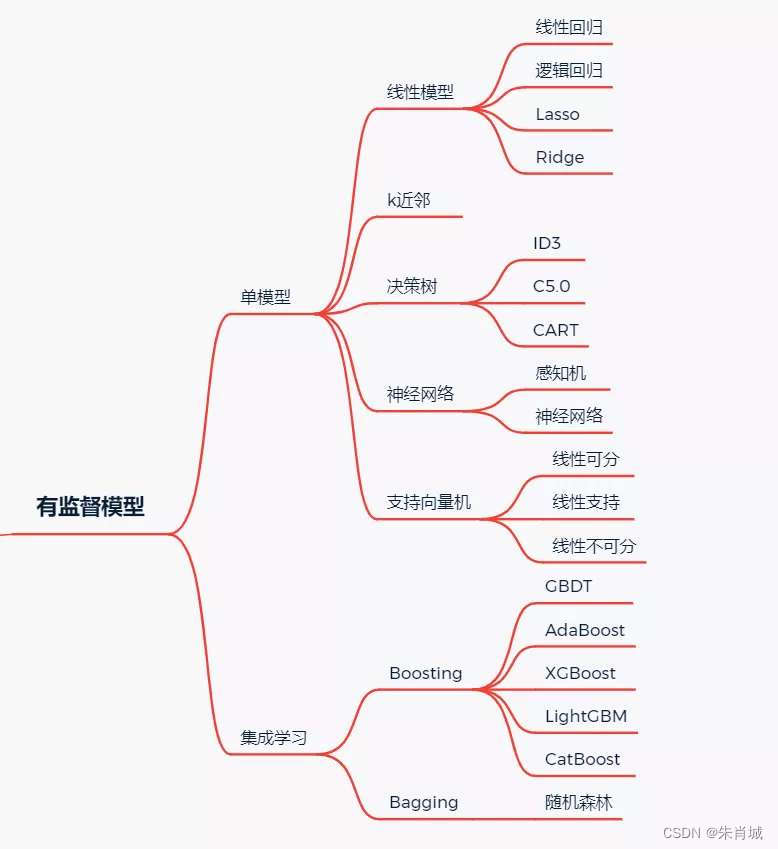
1.2 無監督學習模型

?1.3 概率模型

1.4、什么是監督學習?什么是非監督學習?
?????????所有的回歸算法和分類算法都屬于監督學習。并且明確的給給出初始值,在訓練集中有特征和標簽,并且通過訓練獲得一個模型,在面對只有特征而沒有標簽的數據時,能進行預測。
????????監督學習:通過已有的一部分輸入數據與輸出數據之間的對應關系,生成一個函數,將輸入映射到合適的輸出,例如 分類。
????????非監督學習:直接對輸入數據集進行建模,例如強化學習、K-means 聚類、自編碼、受限波爾茲曼機。
????????半監督學習:綜合利用有類標的數據和沒有類標的數據,來生成合適的分類函數。
? ????????目前最廣泛被使用的分類器有人工神經網絡、支持向量機、最近鄰居法、高斯混合模型、樸素貝葉斯方法、決策樹和徑向基函數分類。
?????????無監督學習里典型的例子就是聚類了。聚類的目的在于把相似的東西聚在一起,一個聚類算法通常只需要知道如何計算相似度就可以開始工作了。
1.5、回歸、分類、聚類的區別與聯系

1.6、生成模式 vs 判別模式
????????生成模型: 由數據學得聯合概率分布函數 P(X,Y),求出條件概率分布P(Y|X)的預測模型。 樸素貝葉斯、隱馬爾可夫模型、高斯混合模型、文檔主題生成模型(LDA)、限制玻爾茲曼機。 ????????判別式模型: 由數據直接學習決策函數 Y = f(X),或由條件分布概率 P(Y|X)作為預測模型。 K近鄰、SVM、決策樹、感知機、線性判別分析(LDA)、線性回歸、傳統的神經網絡、邏輯斯蒂回歸、boosting、條件隨機場。
2、線性模型
2.1 線性回歸
????????原理: 用線性函數擬合數據,用 MSE 計算損失,然后用梯度下降法(GD)找到一組使 MSE 最小的權重。
????????線性回歸的推導如下所示:
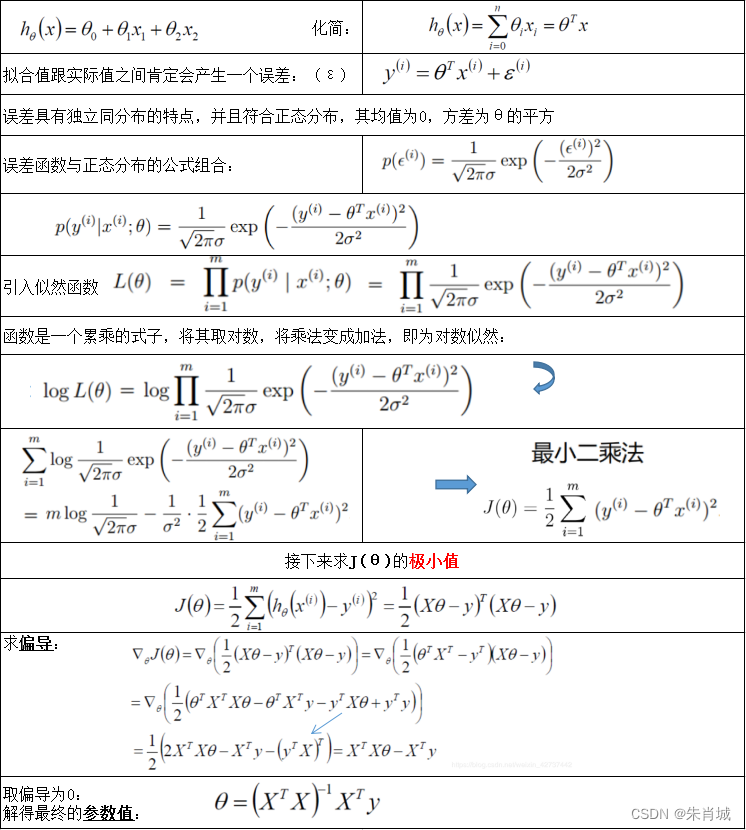
2.1.1 什么是回歸?哪些模型可用于解決回歸問題?
- ????????指分析因變量和自變量之間關系.
- ????????線性回歸: 對異常值非常敏感
- ????????多項式回歸: 如果指數選擇不當,容易過擬合。
- ????????嶺回歸
- ????????Lasso回歸
- ????????彈性網絡回歸
2.1.2 線性回歸的損失函數為什么是均方差?

2.1.3 什么是線性回歸?什么時候使用它?
????????利用最小二乘函數對一個或多個自變量和因變量之間關系進行建模的一種回歸分析.
- 自變量與因變量呈直線關系;
- 因變量符合正態分布;
- 因變量數值之間獨立;
- 方差是否齊性。
2.1.4 什么是梯度下降?SGD的推導?
????????BGD: 遍歷全部數據集計算一次loss函數,然后算函數對各個參數的梯度,更新梯度。?

BGD、SGD、MBGD之間的區別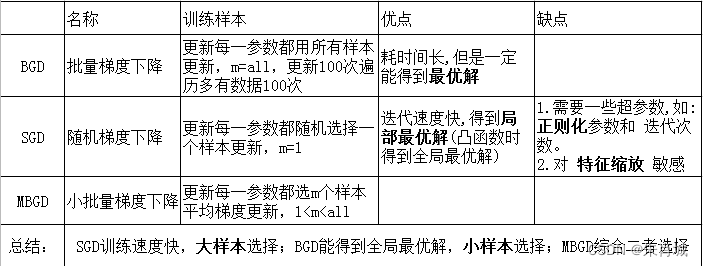

2.1.5 什么是最小二乘法(最小平方法)?
????????它通過最小化誤差的平方和尋找數據的最佳函數匹配。
2.1.6 常見的損失函數有哪些?
- 0-1損失
- 均方差損失(MSE)
- 平均絕對誤差(MAE)
- 分位數損失(Quantile Loss)
- 分位數回歸可以通過給定不同的分位點,擬合目標值的不同分位數; 實現了分別用不同的系數控制高估和低估的損失,進而實現分位數回歸
- 交叉熵損失
- 合頁損失 一種二分類損失函數,SVM的損失函數本質: Hinge Loss + L2 正則化 合頁損失的公式如下:
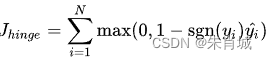
2.1.7 有哪些評估回歸模型的指標?
????????衡量線性回歸法最好的指標: R-Squared

?2.1.8?什么是正規方程??
????????正規方程組是根據最小二乘法原理得到的關于參數估計值的線性方程組。正規方程是通過求解![]() 來找出使得代價函數最小的參數解出:
來找出使得代價函數最小的參數解出: ![]()
2.1.9?梯度下降法找到的一定是下降最快的方向嗎?
????????不一定,它只是目標函數在當前的點的切平面上下降最快的方向。 在實際執行期中,牛頓方向(考慮海森矩陣)才一般被認為是下降最快的方向,可以達到超線性的收斂速度。梯度下降類的算法的收斂速度一般是線性甚至次線性的(在某些帶復雜約束的問題)。
2.1.10 MBGD需要注意什么? 如何選擇m?
????????一般m取2的冪次方能充分利用矩陣運算操作。 一般會在每次遍歷訓練數據之前,先對所有的數據進行隨機排序,然后在每次迭代時按照順序挑選m個訓練集數據直至遍歷完所有的數據。
2.2 LR
也稱為"對數幾率回歸"。
知識點提煉
- ??? 1.分類,經典的二分類算法!
- ??? 2.LR的過程:面對一個回歸或者分類問題,建立代價函數,然后通過優化方法迭代求解出最優的模型參數,然后測試驗證這個求解的模型的好壞。
- ??? 3.Logistic 回歸雖然名字里帶“回歸”,但是它實際上是一種分類方法,主要用于兩分類問題(即輸出只有兩種,分別代表兩個類別)
- ??? 4.回歸模型中,y 是一個定性變量,比如 y = 0 或 1,logistic 方法主要應用于研究某些事件發生的概率。
- ??? 5.LR的本質:極大似然估計
- ??? 6.LR的激活函數:Sigmoid
- ??? 7.LR的代價函數:交叉熵
優點:
- ??? 1.速度快,適合二分類問題
- ??? 2.簡單易于理解,直接看到各個特征的權重
- ??? 3.能容易地更新模型吸收新的數據
缺點:
- ?? 對數據和場景的適應能力有局限性,不如決策樹算法適應性那么強。LR中最核心的概念是 Sigmoid 函數,Sigmoid函數可以看成LR的激活函數。
- Regression 常規步驟:
- ??? 尋找h函數(即預測函數)
- ??? 構造J函數(損失函數)
- ??? 想辦法(迭代)使得J函數最小并求得回歸參數(θ)
LR偽代碼:
- ??? 初始化線性函數參數為1
- ??? 構造sigmoid函數
- ??? 重復循環I次
- ??? ??????? 計算數據集梯度
- ??? ??????? 更新線性函數參數
- ??? 確定最終的sigmoid函數
- ??? 輸入訓練(測試)數據集
- ??? 運用最終sigmoid函數求解分類

2.2.1?為什么 LR 要使用 sigmoid 函數?
????????1.廣義模型推導所得 2.滿足統計的最大熵模型 3.性質優秀,方便使用(Sigmoid函數是平滑的,而且任意階可導,一階二階導數可以直接由函數值得到不用進行求導,這在實現中很實用)
2.2.2?為什么常常要做特征組合(特征交叉)?
- ????????LR模型屬于線性模型,線性模型不能很好處理非線性特征,特征組合可以引入非線性特征,提升模型的表達能力。
- ????????另外,基本特征可以認為是全局建模,組合特征更加精細,是個性化建模,但對全局建模會對部分樣本有偏,
- ????????對每一個樣本建模又會導致數據爆炸,過擬合,所以基本特征+特征組合兼顧了全局和個性化。
2.2.3?為什么LR比線性回歸要好?
- ????????LR和線性回歸首先都是廣義的線性回歸;其次經典線性模型的優化目標函數是最小二乘,而LR則是似然函數;另外線性回歸在整個實數域范圍內進行預測,敏感度一致,而分類范圍,需要在[0,1]。LR就是一種減小預測范圍,將預測值限定為[0,1]間的一種回歸模型,因而對于這類問題來說,LR的魯棒性比線性回歸的要好
2.2.4 LR參數求解的優化方法?(機器學習中常用的最優化方法)
????????梯度下降法,隨機梯度下降法,牛頓法,擬牛頓法(LBFGS,BFGS,OWLQN)
????????目的都是求解某個函數的極小值。
2.2.5?工程上,怎么實現LR的并行化?有哪些并行化的工具?
- ????????LR的并行化最主要的就是對目標函數梯度計算的并行化。
- ????????無損的并行化:算法天然可以并行,并行只是提高了計算的速度和解決問題的規模,但和正常執行的結果是一樣的。
- ????????有損的并行化:算法本身不是天然并行的,需要對算法做一些近似來實現并行化,這樣并行化之后的雙方和正常執行的結果并不一致,但是相似的。
- ????????基于Batch的算法都是可以進行無損的并行化的。而基于SGD的算法都只能進行有損的并行化。
2.2.6 LR如何解決低維不可分問題?
????????通過特征變換的方式把低維空間轉換到高維空間,而在低維空間不可分的數據,到高維空間中線性可分的幾率會高一些。
????????具體方法:核函數,如:高斯核,多項式核等等
2.2.7 LR與最大熵模型MaxEnt的關系?
????????沒有本質區別。LR是最大熵對應類別為二類時的特殊情況,也就是當LR類別擴展到多類別時,就是最大熵模型。
2.2.8 為什么 LR 用交叉熵損失而不是平方損失(MSE)?
![]()
????????如果使用均方差作為損失函數,求得的梯度受到sigmoid函數導數的影響;
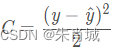 求導:
求導:![]()
????????如果使用交叉熵作為損失函數,沒有受到sigmoid函數導數的影響,且真實值與預測值差別越大,梯度越大,更新的速度也就越快。
![]() 求導:
求導:![]()
????????記憶:mse的導數里面有sigmoid函數的導數,而交叉熵導數里面沒有sigmoid函數的導數,sigmoid的導數的最大值為0.25,更新數據時太慢了。
2.2.9 LR能否解決非線性分類問題?
可以,只要使用kernel trick(核技巧)。不過,通常使用的kernel都是隱式的,也就是找不到顯式地把數據從低維映射到高維的函數,而只能計算高維空間中數據點的內積。
2.2.10 用什么來評估LR模型?
- 1.由于LR是用來預測概率的,可以用AUC-ROC曲線以及混淆矩陣來確定其性能。
- 2.LR中類似于校正R2 的指標是AIC。AIC是對模型系數數量懲罰模型的擬合度量。因此,更偏愛有最小的AIC的模型。
2.2.11 LR如何解決多分類問題?(OvR vs OvO)

2.2.12?在訓練的過程當中,如果有很多的特征高度相關或者說有一個特征重復了100遍,會造成怎樣的影響?
????????如果在損失函數最終收斂的情況下,其實就算有很多特征高度相關也不會影響分類器的效果。但是對特征本身來說的話,假設只有一個特征,在不考慮采樣的情況下,你現在將它重復100遍。訓練以后完以后,數據還是這么多,但是這個特征本身重復了100遍,實質上將原來的特征分成了100份,每一個特征都是原來特征權重值的百分之一。如果在隨機采樣的情況下,其實訓練收斂完以后,還是可以認為這100個特征和原來那一個特征扮演的效果一樣,只是可能中間很多特征的值正負相消了。
2.2.13?為什么在訓練的過程當中將高度相關的特征去掉?
- ????????去掉高度相關的特征會讓模型的可解釋性更好。
- ? ? ? ?可以大大提高訓練的速度。如果模型當中有很多特征高度相關的話,就算損失函數本身收斂了,但實際上參數是沒有收斂的,這樣會拉低訓練的速度。
- ? ? ? ? 其次是特征多了,本身就會增大訓練的時間。
2.3 Lasso
????????定義:所有參數絕對值之和,即L1范數,對應的回歸方法。
Lasso(alpha=0.1)? # 設置學習率
2.4 Ridge
- 定義:所有參數平方和,即L2范數,對應的回歸方法。
- 通過對系數的大小施加懲罰來解決 普通最小二乘法 的一些問題。
- Ridge(alpha=0.1)?? # 設置懲罰項系數
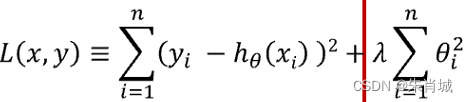
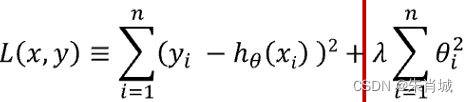
2.5 Lasso vs Ridge

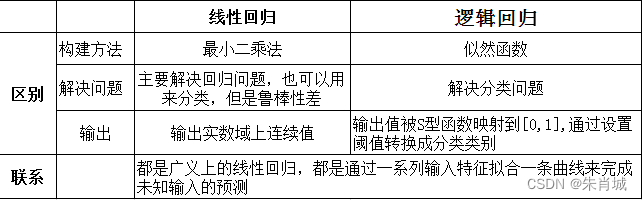
2.6 線性回歸 vs LR
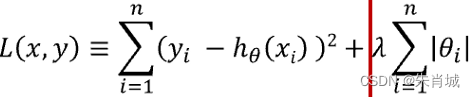
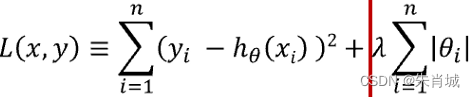

——二叉樹)






)




)



)
進程等待)