模板 :?

?個人傾向第一種 ;

?

?

?

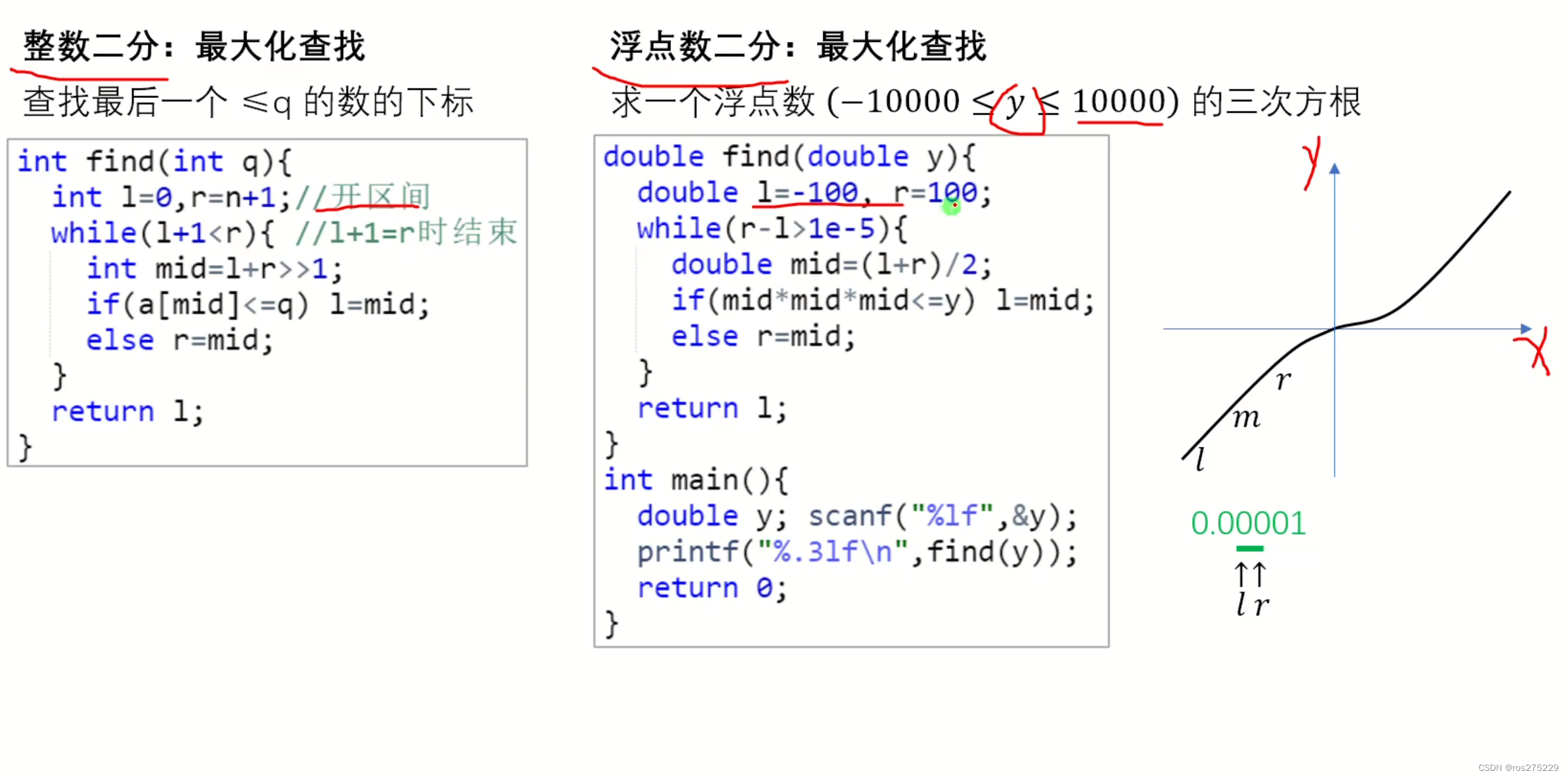
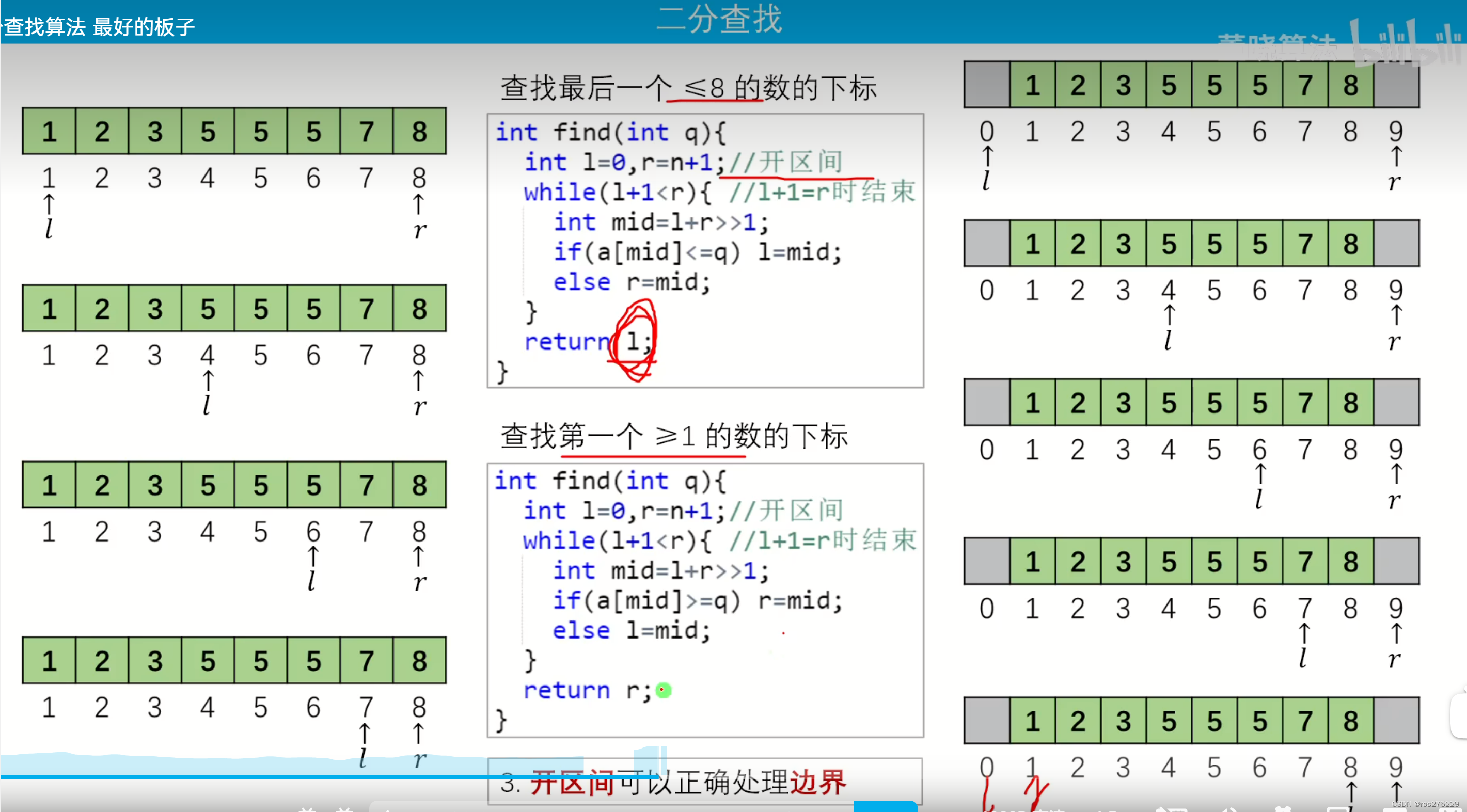
?整數二分 :?

最大化查找 :

可行區域在左側 : 查找最后一個<=q的數的下標 :?

int find(int q){// 查找最后一個 <= q 的下標 int l = 0 , r = n + 1 ;while(l + 1 < r){int mid = l + r >> 1 ;if(a[mid]<=q) l = mid ;else r = mid ;}return l ;
}

?最小化查找 :?

可行區域在右側 : 查找第一個>=q的數的下標 :
?

int find(int q){ // 查找第一個>=q的下標 int l = 0 , r = n + 1 ;while(l + 1 < r){int mid = l + r >> 1 ;if(a[mid]>=q) r = mid ;else l = mid ;}return r;
}

浮點數二分 :?

double find(double l, double r){const double eps = 1e-6; // eps 表示精度，取決于題目對精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}

以求一個浮點數(-10000 <= y <= 10000) 的三次方根 為例:

double find(double y){ // 最大化查找 double l = -100 , r = 100 ;while(r-l>1e-5){double mid = (l + r) / 2 ;if(mid * mid * mid <= y) l = mid;else r = mid ;}return l ;
} 

例題 :?

35 . 搜索插入位置

. - 力扣（LeetCode）

最小化查找 :?

class Solution {
public:int searchInsert(vector<int>& nums, int target) {// 第一個 >= target 的下標int n = nums.size() ;int l = -1 , r = n ;while(l + 1 < r){// l + 1 == n 結束int mid = l + r >> 1 ;if(nums[mid]>=target) r = mid ;else l = mid ;}// nums[r] ;return r ; }
};

P2249 【深基13.例1】查找

【深基13.例1】查找 - 洛谷

最小化查找 :?

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
int a[N] ;
int main(){int n , m ; cin >> n >> m ; for(int i=1;i<=n;i++) cin >> a[i] ;while(m--){int q ; cin >> q ;int l = 0 , r = n + 1 ;while(l + 1 < r){int mid = l + r >> 1 ;if(a[mid] >= q) r = mid ;else l = mid ;}if(a[r]==q) cout << r << " " ;else cout << -1 << " " ;}
}

P1024 [NOIP2001 提高組] 一元三次方程求解

[NOIP2001 提高組] 一元三次方程求解 - 洛谷

浮點數二分 :?

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;double a , b , c , d ; double f(double x){return a * x * x * x + b * x * x + c * x + d ;	
}double find(double l , double r){while(r-l>0.0001){double mid = (l + r) / 2 ;if(f(mid) * f(r) < 0) l = mid ;else r = mid ;}return l ;
}int main(){cin >> a >> b >> c >> d ;for(int i=-100;i<100;i++){double y1 = f(i) , y2 = f(i + 1) ;if(!y1) printf("%.2f ",1.0 * i) ;if(y1 * y2 < 0){printf("%.2f " , find(i , i + 1)) ;}}
}

學習視頻地址 :?

A05 二分查找算法 最好的板子_嗶哩嗶哩_bilibili