在 Excel 中，VLOOKUP 函數默認情況下是不區分大小寫的：

比如下面的案例，直接使用VLOOKUP函數搜索，只會搜索匹配到不區分大小寫的第一個

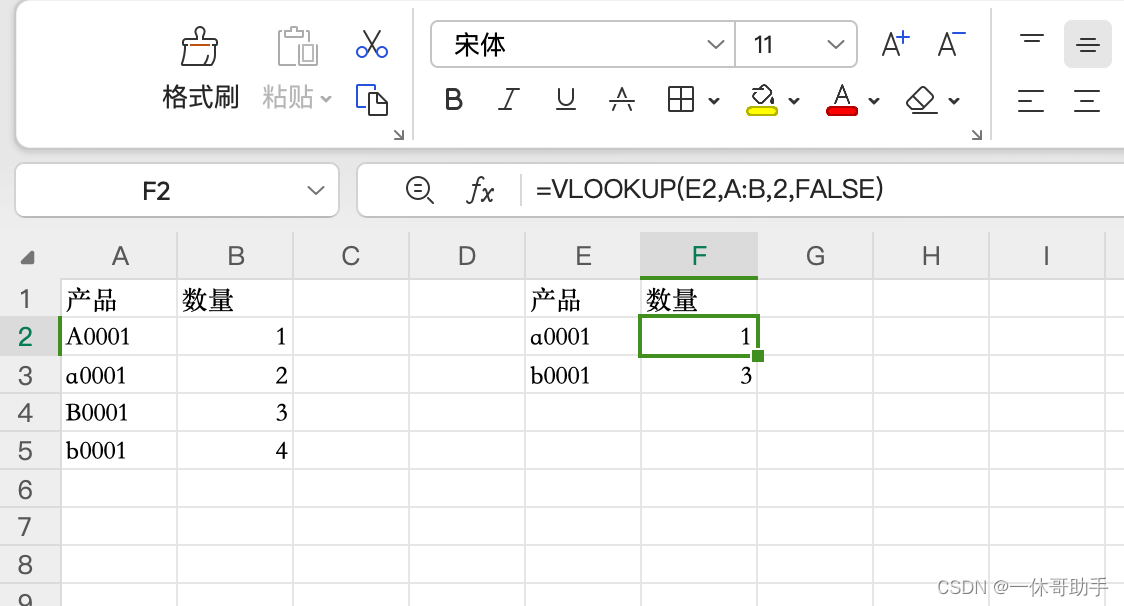
如果我們想要實現區分大小寫的精確匹配，可以使用 EXACT 函數結合 VLOOKUP 函數

（1）先在I2輸入值：=VLOOKUP(H2,IF(EXACT(H2,A:A),A:B),2,FALSE)

（2）然后按 Ctrl + Shift + Enter 組合鍵來將這個公式設為一個數組公式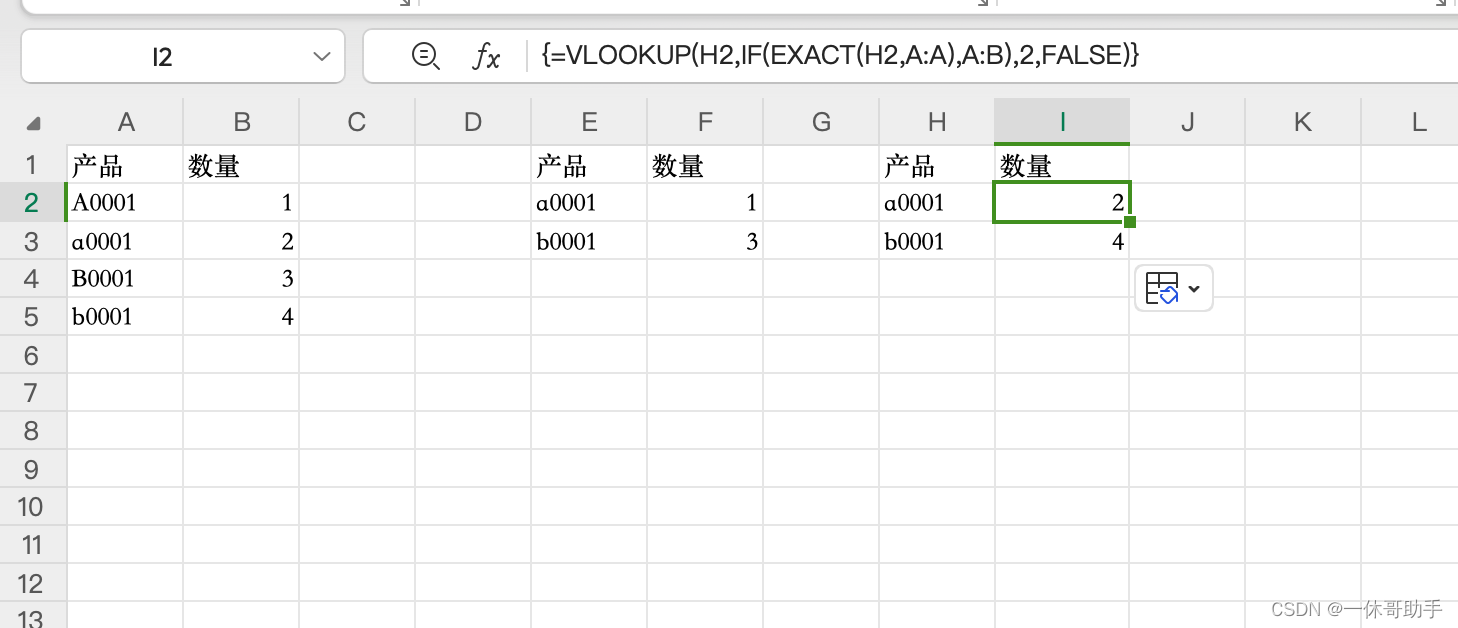

VLOOKUP(H2,IF(EXACT(H2,A:A),A:B),2,FALSE) 的 詳細解釋：

1. EXACT(H2, A:A)：這部分使用 EXACT 函數來比較單元格 H2 中的值與整個 A 列中的值是否完全相同。EXACT 函數會返回一個布爾值，如果兩個值完全相同，則返回 TRUE，否則返回 FALSE。

2. IF(EXACT(H2, A:A), A:B)：這部分使用 IF 函數。如果 H2 和 A 列中的某個值完全相同（即 EXACT 函數返回 TRUE），則 IF 函數返回 A 列和 B 列構成的數組，否則返回 FALSE。

3. VLOOKUP(H2, IF(EXACT(H2, A:A), A:B), 2, FALSE)：最終的 VLOOKUP 函數將在這個數組中查找 H2 的值。如果 H2 與 A 列中的某個值完全相同，則 VLOOKUP 返回相應的 B 列中的值（第二列），否則返回 #N/A（因為 VLOOKUP 的最后一個參數設為 FALSE，表示精確匹配）。