卷積神經網絡

基本結構

首先解釋一下什么是卷積，這個卷積當然不是數學上的卷積，這里的卷積其實表示的是一個三維的權重，這么解釋起來可能不太理解，我們先看看卷積網絡的基本結構。

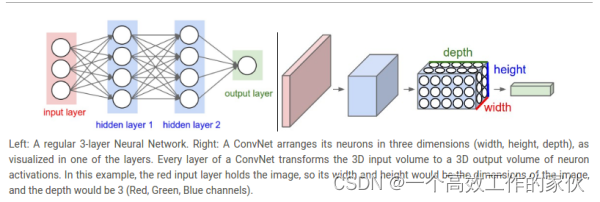
通過上面的圖我們清楚地了解到卷積網絡和一般網絡結構上面的差別，也可以理解為卷積網絡是立體的，而一般的網絡結構是平面的。

卷積層

了解完了基本的結構之后，我們就要了解cnn最重要的一個部分，也是起最為創新的一個部分，卷積層。首先用一張圖片來比較一下卷積網絡到底創新在什么地方。

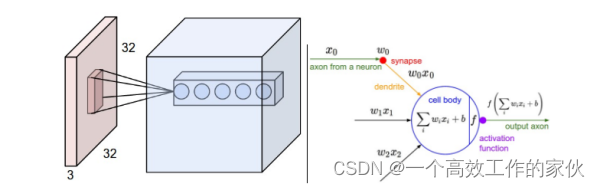
我們通過這個結構就可以清晰地看到卷積網絡到底是怎么實現的。首先右邊是傳統的網絡結構，在上一篇文章中我們已經詳細的解釋過了。而左邊的圖片，我們首先看看圖中最左邊的結構，你肯定會好奇為什么是32x32x3的一塊立體方塊。這個32×32代表的是像素點，說白了也就是圖片的大小，這個大小是你可以設置的，你可以設置為50×50，也可以是256×256，這都取決與圖片的大小，那么3表示什么呢？3其實表示的是RGB的三個通道，RGB也是什么？RGB表示red，green，blue，這三種顏色的各種組合疊加可以形成各種各樣的顏色，所以任何一張照片都可以用左邊這種圖形來表示。

那么中間這個小方塊又表示什么呢？這個就是我們要重點講的卷積。所謂的卷積，就是這種小方塊，我們設置一個小方塊的大小，但是這個小方塊的厚度必須和左邊的這個大方塊的厚度是一樣的，大方塊每一個像素點由一個0到255的數字表示，這樣我們就可以賦予小方塊權重，比如我們取小方塊的大小是3×3，我們要求起厚度必須要和左邊的大方塊厚度一樣，那么小方塊的的大小就為3x3x3，我們就可以賦予其3x3x3個權重，然后我們就可以開始計算卷積的結果，將小方塊從大方塊的左上角開始，一個卷積小方塊所覆蓋的范圍是3x3x3，然后我們將大方塊中3x3x3的數字和小方塊中的權重分別相乘相加，再加上一個偏差，就可以得到一個卷積的接過，可以抽象的寫成Wx b這種形式，這就是圖上所顯示的接過，然后我們可以設置小方塊的滑動距離，每次滑動就可以形成一個卷積的計算結果，然后講整張大圖片滑動覆蓋之后就可以形成一層卷積的結果，我們看到圖中的卷積結果是很厚的，也就是設置了很多層卷積。總結來說，就是每層卷積就是一個卷積核在圖片上滑動求值，然后設置多個卷積核就可以形成多層的卷積層。

池化層

講完卷積層，接下來就要講一下池化層。為什么會有池化層的出現呢？是因為不斷的做卷積，得到的中間結果會越來越厚，卷積就相當于提取圖片中的特征，所以卷積層一般會設置得越來越厚，不然你就無法從前面的接過來提取更多的特征。這樣就會導致中間的結果會越來越大，計算會越來越慢，所以提出了池化層。

所謂的池化層，就是將圖片的大小縮小的一種處理方式。我們可以先看看下面的圖片。

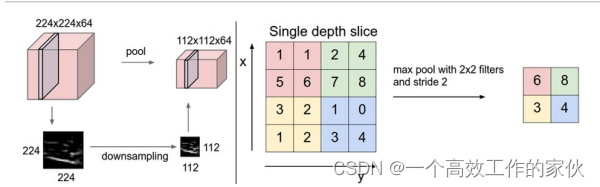
通過這個圖片，我們可以清楚地看到池化層是怎么處理的。池化層也是需要先設置一個窗口，但是這個小窗口的厚度是1，而不再是前一層輸出的結果的厚度。然后有兩種處理方式，一種是取這個小窗口里面所有元素的最大值來代表這個小窗口，一種是取平均值，然后將小窗口滑動，在第二的位置再做同樣的處理，上層網絡輸出方塊的每一層做完之后就進入這個大方塊的下一層做同樣的操作，這個處理辦法就可以讓整個大方塊的大小變小，可以看看上面的圖片的左邊。右邊是一個簡單的一層厚度，取最大值的例子。

Code

數據集仍然是使用MNIST手寫字體，和之前一樣做同樣的預處理。

Model

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

# 定義 Convolution Network 模型 class Cnn(nn.Module): ????def __init__(self, in_dim, n_class): ????????super(Cnn, self).__init__() ????????self.conv = nn.Sequential( ????????????nn.Conv2d(in_dim, 6, 3, stride=1, padding=1), ????????????nn.ReLU(True), ????????????nn.MaxPool2d(2, 2), ????????????nn.Conv2d(6, 16, 5, stride=1, padding=0), ????????????nn.ReLU(True), ????????????nn.MaxPool2d(2, 2), ????????) ????????self.fc = nn.Sequential( ????????????nn.Linear(400, 120), ????????????nn.Linear(120, 84), ????????????nn.Linear(84, n_class) ????????) ????def forward(self, x): ????????out = self.conv(x) ????????out = out.view(out.size(0), -1) ????????out = self.fc(out) ????????return out model = Cnn(1, 10)??# 圖片大小是28x28 use_gpu = torch.cuda.is_available()??# 判斷是否有GPU加速 if use_gpu: ????model = model.cuda() # 定義loss和optimizer criterion = nn.CrossEntropyLoss() optimizer = optim.SGD(model.parameters(), lr=learning_rate)

以上就是網絡的模型的部分了。和之前比主要增加了這些不一樣的部分

• 1?nn.Sequential()
  這個表示將一個有序的模塊寫在一起，也就相當于將神經網絡的層按順序放在一起，這樣可以方便結構顯示
• 2 nn.Conv2d()
  這個是卷積層，里面常用的參數有四個，in_channels, out_channels, kernel_size, stride, padding
  in_channels表示的是輸入卷積層的圖片厚度

  out_channels表示的是要輸出的厚度

  kernel_size表示的是卷積核的大小，可以用一個數字表示長寬相等的卷積核，比如kernel_size=3，也可以用不同的數字表示長寬不同的卷積核，比如kernel_size=(3, 2)

  stride表示卷積核滑動的步長

  padding表示的是在圖片周圍填充0的多少，padding=0表示不填充，padding=1四周都填充1維

• 3 nn.ReLU()
  這個表示使用ReLU激活函數，里面有一個參數inplace，默認設置為False，表示新創建一個對象對其修改，也可以設置為True，表示直接對這個對象進行修改
• 4 nn.MaxPool2d()
  這個是最大池化層，當然也有平均池化層，里面的參數有kernel_size, stride, padding

  kernel_size表示池化的窗口大小，和卷積層里面的kernel_size是一樣的

  stride也和卷積層里面一樣，需要自己設置滑動步長

  padding也和卷積層里面的參數是一樣的，默認是0

  模型需要傳入的參數是輸入的圖片維數以及輸出的種類數

train

訓練的過程是一樣的，只是輸入圖片不再需要展開

這是訓練20個epoch的結果，當然你也可以增加訓練次數，修改里面的參數達到更好的效果，可以參考一下Lenet的網絡結構，自己重新寫一寫

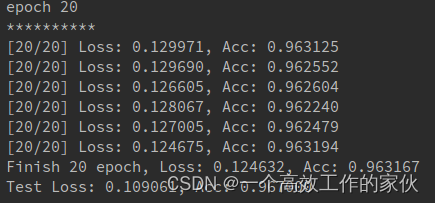
大體上簡單的卷積網絡就是這么構建的，當然現在也有很多復雜的網絡，比如vgg，inceptionv1-v4，resnet以及修正的inception-resnet，這些網絡都是深層的卷積網絡，有興趣的同學可以去看看pytorch的官方代碼實現，或者去github上搜索相應的網絡。

下一節我們將要開始一種特別適合序列數據的新的網絡結構，循環神經網絡。