【算法集訓】基礎算法：枚舉

一、基本理解

枚舉的概念就是把滿足題目條件的所有情況都列舉出來，然后一一判定，找到最優解的過程。
枚舉雖然看起來麻煩，但是有時效率上比排序高，也是一個不錯的方法、

二、最值問題

1、兩個數的最值問題

兩個數的最小值，利用C語言中的三元運算符就可以實現：

int Min(int a, int b) {
return a < b ? a : b;
}

2、n 個數的最值問題

當有 n 個數時 ai 時，我們可以首先取前兩個數，計算最小值；然后再拿這個最小值和第三個數去比較，得到的最小值再去和第四個數比較，以此類推，就可以計算出 n 個數中的最小值。
假設前 i 個數的最小值為 mi，則有遞推公式如下：

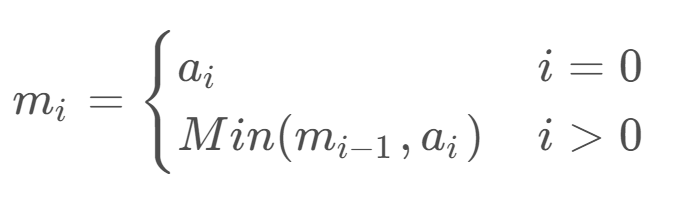
所以，把這個遞推公式翻譯成C語言，代碼是這樣的：

int Min(int a, int b) {
return a < b ? a : b;
}
int NMin(int* a, int n){
int *m = (int *) malloc( sizeof(int) * numsSize );
int m[0] = a[0];
for(int i = 1; i < n; ++i) {
m[i] = Min(m[i-1], a[i]);
}
int ret = m[n-1];
free(m);
return ret;
}

而這里的 m[i] 和 m[i-1] 可以利用迭代，存儲在一個變量中，用 C語言實現如下：

int Min(int a, int b) {
return a < b ? a : b;
}
int NMin(int* a, int n){
int m = a[0];
for(int i = 1; i < n; ++i) {
m = Min(m, a[i]);
}
return m;
}

3、最值問題的下標

當然，有些時候，我們求的并不是一個最小的數，要是要求出這個數組中，最小的數的下標，那么可以直接記錄下標，并且比較的時候直接通過下標去索引到值，然后進行比較，像這樣：
int NMin(int* a, int n){
int mIdx = 0;
for(int i = 1; i < n; ++i) {
if( a[i] < a[mIdx] ) {
mIdx = i;
}
}
return mIdx;
}
可以嘗試做一下這道題，鞏固一下概念：https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/

三、最值問題的進階

1、第三大的數

有時候，我們求最大的數不夠，想要求次大的，甚至第三大的，比如 1 2 2 3 中第三大的是 1 （相同的數只計算一次）。
這樣的問題，核心思路就是先把最大的求出來；然后忽略最大的數的情況下，再去求最大的；這時候就得到了次大的，再把次大的也忽略以后，再求最大的，自然就是第三大的了。
第三大的數 - 視頻講解。

2、數組中兩元素的最大乘積

要求找到數組中兩個元素的最大乘積，數組元素一定是正數。那么我們知道最大的兩個元素相乘一定是最大的，所以就是找最大的元素和次大的元素，但是這個問題和第三大的數略微有些不同，相同的數會被計算進去。
所以，我們找到最大的數以后，可以把它的下標忽略掉；然后再去找最大的數，這樣找到的一定是兩個可重復的最大元素和次大元素，將兩者相乘即可。
當然有同學就要問了，那我是不是直接把數組按照遞增排序，然后取最后兩個元素相乘就可以了。是的，也可以，但是比較排序的最優時間復雜度為 O(nlogn)，而找兩次最大值的時間復雜度為 O(n)。

四、降維思想

一些統計類問題，第一個思路就是枚舉所有情況（也就是多個 for 循環），然后再去考慮是不是能夠把某些 for 循環的 O(n) 的時間復雜度降為 O(1)，這個就是降維的思想。來看這個經典問題：
這個問題能自己想出來，就達到了 ACM 區域賽銅牌的水平。
給你一個長度為 n (n ≤ 4000) 下標從 0 開始的整數數組 nums ，它包含 1 到 n 的所有數字，請你返回上升四元組的數目。如果一個四元組 (i, j, k, l) 滿足以下條件，我們稱它是上升的：
1）0 <= i < j < k < l < n 且
2）nums[i] < nums[k] < nums[j] < nums[l] 。

1、O(n^4)

首先，最壞時間復雜度的算法，相信大家都能想出來，就是枚舉 i、j、k、l 四個變量，然后判斷 nums 四個數的關系，進行統計累加，這種情況下，最壞的時間復雜度為 O(n^4)，由于 n 為 4000。
也就是相當于 n = 16000000 的數據量下，用 O(n^2) 的算法去求解問題，所以必然超時。

2、O(n^3)

如果要用 O(n^3) 的算法求解，你會怎么去思考呢？如果有想法，可以寫好以后附在評論區。

3、O(n^2)

是的，由于 n 的范圍限制，就算你想出了 O(n^3) 的算法，還是過不了這個問題，我們需要繼續想 O(n^2) 的算法。
算法思路如下：
1、首先，我們枚舉 j 和 k，然后對所有滿足 nums[j] > nums[k] 的下標對，執行下一步。
2、那么只要我們找到數組下標為 0 到 j-1 的數中，小于 nums[k] 的個數，記為 a（也就是所有滿足條件的 i）；找到數組下標為 k+1 到 n-1 的數中，大于 nums[j] 的個數，記為 b（也就是所有滿足條件的）；將 a * b 就是所有滿足條件的 (i, l) 對，把所有的（i, l）數對累加，就是我們最后要求的答案了。
3、于是問題轉變成了求找到數組下標為 0 到 j-1 的數中，小于 nums[k] 的個數和找到數組下標為 k+1 到 n-1 的數中，大于 nums[j] 的個數；
4、定義兩個輔助數組 less[4001][4001] 和 bigger[4001][4001]，令 less[i][j] 表示前 i-1 個數中，小于 j 的數的個數；令 bigger[i][j] 表示 i 以后（不包括 i）的數中，大于 j 的數的個數。less 和 bigger 的含義類似，通過兩個 for 循環枚舉求出 less 和 bigger。
5、最后，只要枚舉 j 和 k，在滿足 nums[j] > nums[k] 的條件下，累加 less[j][ nums[k] * bigger[k][nums[j]] 的和，就是我們要求的解了。

五、題目練習

2656. K 個元素的最大和

int maximizeSum(int* nums, int numsSize, int k){int max = 0;for(int i = 0; i < numsSize; ++i) {if(nums[i] > max) {max = nums[i];}}int ans = max;while(--k) {ans += max + 1;max += 1;}return ans;
}

414. 第三大的數

#define INF -213214121int thirdMax(int* nums, int numsSize){// 找最大值int max = nums[0];for(int i = 1; i < numsSize; ++i) {if(max < nums[i]) {max = nums[i];}}// 找第二大的數int subMax = INF;for(int i = 0; i < numsSize; ++i) {if(subMax == INF) {if(nums[i] < max) subMax = nums[i];}else {if(nums[i] > subMax && nums[i] < max) {subMax = nums[i];}}}//不存在第二大的,返回第一大的if(subMax == INF) return max;//找第三大的數int triMax = INF;for(int i = 0; i < numsSize; ++i) {if(triMax == INF) {if(nums[i] < subMax) triMax = nums[i];}else {if(nums[i] > triMax && nums[i] < subMax) {triMax = nums[i];}}}if(triMax == INF) return max;return triMax;
}