今日題目:
- 239. 滑動窗口最大值 | LeetCode
今天學習了單調隊列這種特殊的數據結構,思路很新穎,值得學習。
Problem:單調隊列 【必會】
與單調棧類似,單調隊列也是一種特殊的數據結構,它相比與普通的 queue,增加了一個新的接口 max() 來獲取當前隊列的最大值。
新增的 max() 是我們選用這個數據結構的最重要原因,單調隊列不僅僅可以通過 offer() 和 poll() 接口來實現 FIFO 的元素進出順序,還額外增加了 max() 接口讓我們獲取到當前隊列中的最大元素。
單調隊列主要用來解決下面這個場景:我們會時刻向一個集合中增加新元素或減少舊元素,同時每次可以獲取到當前這個集合中的最大值。優先級隊列也可以滿足這個需求,但優先級隊列無法滿足 FIFO 的元素進出順序,這也是必須使用單調隊列的原因。
假如有一個數組
window,并知道它的最大值是 A,此時向 window 增加一個新元素 B,我們只需要比較 A 和 B 就可以得到當前 window 中的最大值;但如果刪除一個舊元素 C,就麻煩了,因為如果這個刪除的 C 恰恰就是最大值 A,那么最大值就要重新遍歷 window 來尋找了,從而導致復雜度飆升。這就是單調隊列所需要解決的難題。
下面看一下單調隊列的經典應用:滑動窗口最大值。
LC 239. 滑動窗口最大值 【classic】 ?????
239. 滑動窗口最大值 | LeetCode
如果我們能夠實現數據結構“單調隊列” MonoQueue,那我們就每次向右滑動我們的窗口時,向 monoQueue 中新增一個窗口右邊的新元素,移除一個窗口左邊的舊元素,然后調用 max() 接口獲取當前窗口的最大值,就可以計算出題目所需要的最終結果。
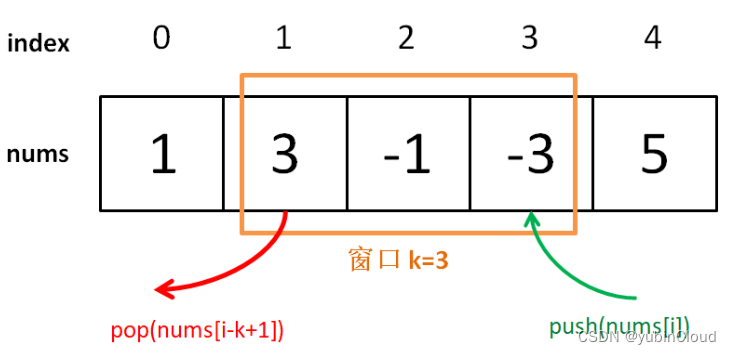
所以重點在于如何實現 MonoQueue。
我們需求的關鍵是:需要能夠快速得知當前隊列中的最大值。由于窗口滑動時是有順序的,先進入的元素一定會先出去,所以如果新進入的一個元素,那么比它老的還比它小的那些元素就永遠不可能成為當前隊列中的最大值了,因為老元素一定會比新元素更早地離開隊列。所以,每次在入隊一個新元素時,就可以把隊列中比他小的元素都拋棄掉了:
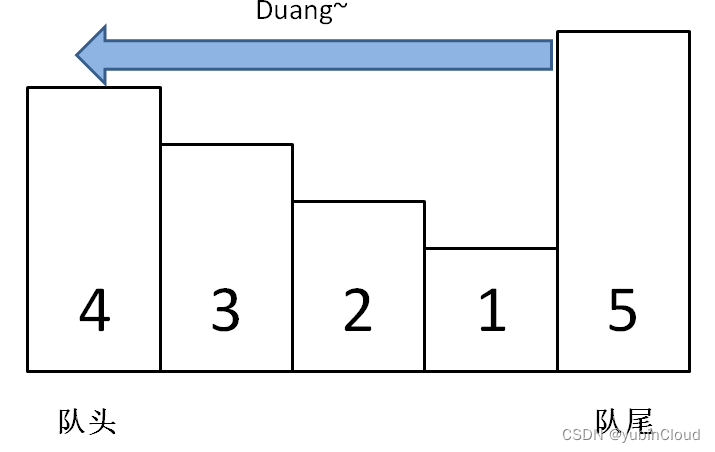
如上圖,當元素 5 進入隊列后,就可以一下子把 4、3、2、1 全給拋棄掉了,因為這些舊元素在隊列的時候 5 一定在,所以這些舊元素一定成不了“當前隊列的最大值”。
根據以上分析,單調隊列 MonoQueue 的實現如下:
class MonoQueue {private Deque<Integer> maxQ = new LinkedList<>();public void offer(int num) {// 將小于 num 的元素全部刪除while (!maxQ.isEmpty() && maxQ.getLast() < num) {maxQ.removeLast();}// 將 num 加入隊尾maxQ.addLast(num);}public int max() {return maxQ.getFirst(); // 單調隊列,隊首就是最大元素}public void poll(int n) {if (maxQ.getFirst() == n) { // 判斷需要移除的是否是隊首,如果不是的話,就是比隊首小還比隊首老的元素,已經被移除了,那就啥也不用干maxQ.removeFirst();}}
}
這里有兩個易錯點:
- 在
offer()函數實現中,第一步刪掉掉小于 num 的元素,但注意別把等于它的元素刪除了,因為如果把相等的元素也刪掉的話,實現poll()接口時,就不太好判斷 隊首最大元素 是否就是我們當前需要 poll 的元素了(我們是通過值相等來判斷的) - 在實現
poll()函數時,其參數 n 表示期待刪除的元素,因為我們這個 MonoQueue 并沒有保留全部入隊元素,所以當需要刪除一個已經被刪除的元素時,poll() 接口只需要立刻返回就可以了。
在實現了 MonoQueue 后,我們解決這個問題就容易多了:
public int[] maxSlidingWindow(int[] nums, int k) {MonoQueue monoQueue = new MonoQueue();List<Integer> result = new ArrayList<>();// 將前 k-1 個元素填充到隊列中for (int i = 0; i < k - 1; i++) {monoQueue.offer(nums[i]);}for (int i = k - 1; i < nums.length; i++) {// 加入窗口右邊的新元素monoQueue.offer(nums[i]);// 獲取窗口內最大元素,并加入到結果集中result.add(monoQueue.max());// 移除窗口左邊的舊元素monoQueue.poll(nums[i - k + 1]);}return result.stream().mapToInt(Integer::valueOf).toArray();}
通過這個題,我們可以更加深入地理解單調隊列的具體用法。在有些情況下,我們除了在 MonoQueue 里面維護一個 maxQ 之外,還可以額外維護一個標準的 queue,從而對外表現出正常的 offer() 和 poll() 接口。
)
)




)


 —— 原始 PPO 代碼解讀)



“云計算應用”賽項樣題 2)





