文章解讀與仿真程序復現思路——電網技術EI\CSCD\北大核心《考慮時空相關性的流域水風光多能互補系統高維不確定性場景生成方法》

本專欄欄目提供文章與程序復現思路，具體已有的論文與論文源程序可翻閱本博主免費的專欄欄目《論文與完整程序》

論文與完整源程序_電網論文源程序的博客-CSDN博客https://blog.csdn.net/liang674027206/category_12531414.html

這篇文章的標題涵蓋了以下幾個關鍵方面：

流域水風光多能互補系統：
- 文章討論的主題涉及一個綜合利用水、風和光能資源的系統，這可能是一種可再生能源系統。這種系統可能包括水力發電、風能發電和光伏發電等多個能源形式，以實現更可靠和可持續的能源供應。
時空相關性：
- 這指的是考慮到時間和空間方面的關聯性。在能源系統中，時空相關性可能涉及到能源產生的季節性、日變化等時間相關性，以及不同地點之間的能源產生差異，即空間相關性。
高維不確定性場景生成方法：
- 文章的重點是在面對高維不確定性的情況下，提出一種場景生成方法。高維不確定性可能源自于多種因素，如氣象條件、市場變動等。場景生成方法用于模擬這些不確定性的情境，以便更好地理解系統行為和做出相應的決策。

因此，整個標題的含義是，這篇文章致力于提出一種方法，用于在流域水風光多能互補系統中，考慮到時空相關性的情況下，生成適應高維不確定性場景的模擬方法。這可能有助于優化多能互補系統的設計、規劃和運營，提高能源系統的魯棒性和可靠性。

摘要：受到變量維度高、時空隨機關聯等復雜因素影響，如何生成年周期的徑流、風電光伏出力耦合場景序列是西南流域水風光一體化多能互補規劃和長期調度面臨的關鍵難題。該文提出一種考慮時空相關性的流域水風光高維耦合不確定性場景生成方法。以基于多年長序列歷史數據為輸入，首先，構建基于季節性馬爾科夫鏈的時序相關性模型，分別捕捉徑流、風光發電能力年內逐月時序狀態轉移特征；其次，構建基于混合Copula函數連接的C藤水風光空間相關性模型，表征流域內水風光異質能源的空間相關特性；以時空相關性建模結果為基礎，結合蒙特卡洛抽樣，提出水風光多能互補系統高維耦合場景集生成方法。最后，以我國金沙江下游梯級電站以及金沙江下游區域內風光電站為應用實例，對比驗證了所提方法的有效性。

這段摘要討論了一項針對西南流域水風光一體化多能互補規劃和長期調度中的關鍵難題的研究。主要內容如下：

問題描述：
- 提到了西南流域水風光一體化多能互補系統在規劃和調度過程中面臨的挑戰，其中之一是生成年周期的徑流、風電和光伏出力的耦合場景序列。
方法提出：
- 作者提出了一種新的方法來解決這一問題，即考慮時空相關性的場景生成方法。
- 這個方法首先利用多年長序列歷史數據作為輸入，構建了基于季節性馬爾科夫鏈的時序相關性模型。這個模型被用來捕捉徑流、風電和光伏發電能力在年內逐月的時序狀態轉移特征。
- 其次，作者構建了基于混合Copula函數連接的C藤水風光空間相關性模型，以表征流域內水、風、光這些異質能源的空間相關特性。
- 最后，結合蒙特卡洛抽樣技術，基于時空相關性建模結果，提出了水風光多能互補系統高維耦合場景集的生成方法。
應用實例：
- 文章最后通過以中國金沙江下游梯級電站和該區域內風光電站為案例，對提出的方法進行了對比驗證，證明了該方法的有效性。

綜合來看，這項研究提出了一種新穎的方法來解決水風光多能互補系統中的關鍵問題，通過考慮時空相關性，能夠更準確地生成高維耦合場景集，為系統規劃和調度提供了有力支持。

關鍵詞：?? ?多能互補系統;時空相關性;場景生成;馬爾科夫鏈;Copula函數;

關鍵詞解讀：

多能互補系統：
- 這指的是一種能源系統，其中多種能源形式相互補充和整合，以提高系統的穩定性、可靠性和效率。在這個背景下，可能包括水能、風能和太陽能等多種可再生能源形式。
時空相關性：
- 指的是時間和空間之間的關聯或相關性。在這個文本中，可能指的是在一個區域內，不同時間點和不同空間點之間的能源生產和消耗之間的關聯關系。
場景生成：
- 這指的是根據一定的模型和算法，生成符合特定條件或模式的數據集合。在這里特指生成水、風、光等能源在不同時間和空間上的產出情況的數據集合。
馬爾科夫鏈：
- 馬爾科夫鏈是一種隨機過程，具有"無記憶性"的性質，即未來的狀態僅僅取決于當前狀態，與過去的狀態無關。在這里，可能用來模擬和捕捉徑流、風電和光伏發電能力在時間序列上的狀態轉移特征。
Copula函數：
- Copula函數是一種用于描述隨機變量之間依賴關系的工具。在這個背景下，可能用來構建描述水、風、光等能源之間空間相關性的模型。

這些關鍵詞在摘要中一起描述了一個方法：利用馬爾科夫鏈模型來捕捉時間序列上的相關性，使用Copula函數來描述能源之間的空間相關性，從而生成多能互補系統中水、風、光等能源在時空上的耦合場景數據集。這個方法旨在應對西南流域水風光一體化多能互補規劃和長期調度中的挑戰。

仿真算例：

在生成水風光考慮時空相關性的場景集之前，需要生成考慮時間相關性的長期場景集，其主要思想為按照1.1節所述步驟構建馬爾科夫鏈模型，再依據蒙特卡洛抽樣生成具有時間相關性的多能互補系統場景集。本文構建包含時間相關性、空間相關性、隨機性以及波動性的場景評價體系，評估所生成的徑流以及風電光伏出力場景集的有效性。采用自相關性系數(Autocorrelation Function, ACF)，平均Kendall 系數絕對誤差(Mean Kendall Correlation Coefficient Absolute Error, MKAE)，歐式距離平均值(Average Euclidean Distance, AED)和覆蓋率這四種指標進行評價。

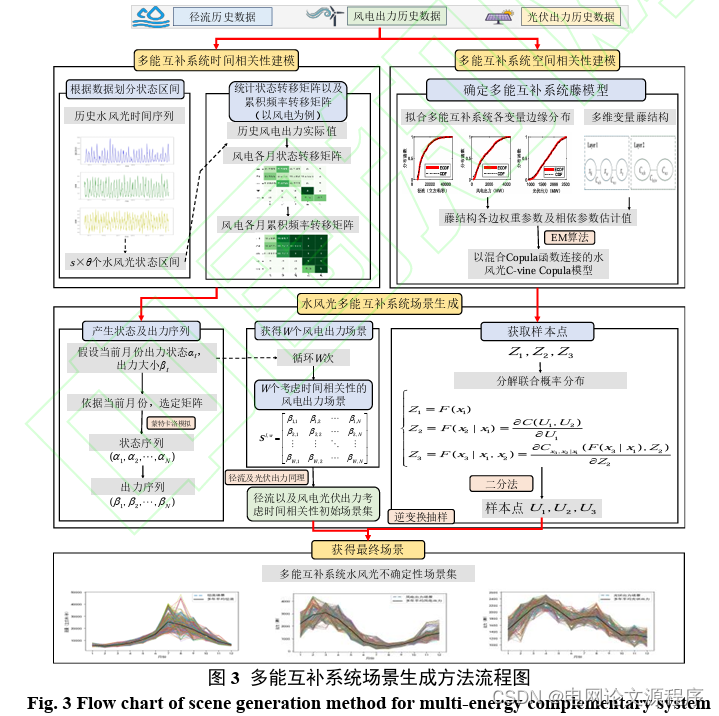
仿真程序復現思路：

當復現生成考慮時間相關性的長期場景集時，我們需要實現馬爾科夫鏈模型的構建以及蒙特卡洛抽樣生成多能互補系統場景集的過程。下面是一個更詳細、更長的Python代碼示例：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal# 步驟1：構建馬爾科夫鏈模型
def build_markov_chain(initial_state, transition_matrix, num_steps):current_state = initial_statestates = [current_state]for _ in range(num_steps):current_state = np.random.choice(len(transition_matrix), p=transition_matrix[current_state])states.append(current_state)return states# 步驟2：蒙特卡洛抽樣生成多能互補系統場景集
def monte_carlo_sampling(mean, covariance_matrix, num_samples):samples = np.random.multivariate_normal(mean, covariance_matrix, size=num_samples)return samples# 示例參數
initial_state = 0  # 初始狀態
transition_matrix = np.array([[0.9, 0.1], [0.2, 0.8]])  # 轉移概率矩陣
mean = np.array([0, 0])  # 均值
covariance_matrix = np.array([[1, 0.5], [0.5, 1]])  # 協方差矩陣
num_steps = 100  # 模擬步數
num_samples = 1000  # 抽樣數量# 生成馬爾科夫鏈模型
states = build_markov_chain(initial_state, transition_matrix, num_steps)# 生成蒙特卡洛抽樣
samples = monte_carlo_sampling(mean, covariance_matrix, num_samples)# 繪制馬爾科夫鏈狀態序列
plt.figure(figsize=(10, 5))
plt.plot(states, marker='o', linestyle='-')
plt.title('Markov Chain State Sequence')
plt.xlabel('Time Step')
plt.ylabel('State')
plt.grid(True)
plt.show()# 繪制蒙特卡洛抽樣結果分布
plt.figure(figsize=(8, 6))
plt.scatter(samples[:, 0], samples[:, 1], alpha=0.5)
plt.title('Monte Carlo Sampling Results')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()# 輸出結果示例
print("馬爾科夫鏈模型狀態序列：", states)
print("蒙特卡洛抽樣場景集：", samples)

這個示例代碼包括了以下幾個部分：

定義了構建馬爾科夫鏈模型的函數build_markov_chain，以及蒙特卡洛抽樣生成多能互補系統場景集的函數monte_carlo_sampling。
使用示例參數初始化了模型所需的參數，如初始狀態、轉移概率矩陣、均值、協方差矩陣等。
調用馬爾科夫鏈模型函數和蒙特卡洛抽樣函數生成數據，并通過matplotlib庫繪制了馬爾科夫鏈狀態序列和蒙特卡洛抽樣結果分布圖。
最后，輸出了馬爾科夫鏈模型的狀態序列和蒙特卡洛抽樣得到的場景集。

這個示例展示了如何使用Python編程語言實現生成考慮時間相關性的長期場景集的仿真過程。

?本專欄欄目提供文章與程序復現思路，具體已有的論文與論文源程序可翻閱本博主免費的專欄欄目《論文與完整程序》

論文與完整源程序_電網論文源程序的博客-CSDN博客https://blog.csdn.net/liang674027206/category_12531414.html