目錄

一，3046. 分割數組

二，3047. 求交集區域內的最大正方形面積

三，3048. 標記所有下標的最早秒數 I

四，3049. 標記所有下標的最早秒數 II

---

一，3046. 分割數組

將題目給的數組nums分成兩個數組，且這兩個數組中沒有相同的元素，求是否存在這兩個數組，即求nums數組中有沒有一個元素的出現次數 > 2，如果大于2，說明不論怎么分配總有一個數組含有相同的元素，返回 false，否則返回 true

代碼如下：

class Solution {public boolean isPossibleToSplit(int[] nums) {int mx = 0;Map<Integer,Integer> map = new HashMap<>();for(int x : nums){map.put(x, map.getOrDefault(x,0)+1);mx = Math.max(mx, map.get(x));}return mx <= 2;}
}

二，3047. 求交集區域內的最大正方形面積

本題求兩個矩陣的交集區域中最大正方形的面積，關鍵在于求出相交區域的矩陣的長和高：

• 左下角的橫坐標（x軸）：兩個矩陣左下角最大的橫坐標
• 左下角的縱坐標（y軸）：兩個矩陣左下角最大的縱坐標
• 右上角的橫坐標（x軸）：兩個矩陣右上角最小的橫坐標
• 右上角的縱坐標（y軸）：兩個矩陣右上角最小的橫坐標

代碼如下：

class Solution {public long largestSquareArea(int[][] bottomLeft, int[][] topRight) {long ans = 0;int n = bottomLeft.length;for(int i=0; i<n; i++){int[] b1 = bottomLeft[i];int[] t1 = topRight[i];for(int j=i+1; j<n; j++){int[] b2 = bottomLeft[j];int[] t2 = topRight[j];int LMx = Math.min(t1[0], t2[0]);int LMn = Math.max(b1[0], b2[0]);int RMn = Math.max(b1[1], b2[1]);int RMx = Math.min(t1[1], t2[1]);int x = Math.min(LMx-LMn, RMx-RMn);if(x > 0)ans = Math.max(ans,(long)x*x);}}return ans;}
}

三，3048. 標記所有下標的最早秒數 I

二分 + 貪心

本題的題目可以轉換成一個更加簡單易懂的說法 —— 學校考試：

距離學期結束還有 m 天，要復習?n 門課程，第 i 門課程的復習時間是nums[i]，并且每一門課程的考試時間是固定的，由changeIndices數組決定（changIndices[i] 表示可以在第 i 天考第 changIndices[i] 門課程），問要將 n 門課程復習完+考完（考試當天只能用來考試），最少要花費多少時間？

通過讀題，會發現直接求答案是非常困難的，那么是否可以通過枚舉最終所需的天數來判斷它是否夠用，如果夠用，那么縮減天數，如果不夠用，那么增加天數，想到這，自然就會想到二分答案，但是使用二分還有一個前提：要具有單調性，那么本題是否有單調性呢？當然是有的：給的時間越多，復習的時間越充裕，越能夠通過考試。

二分是可以的，那么接下來就是判斷二分的這個答案是否成立（即如何判斷所給的天數是否充足），有兩種思考方式，一種從前往后思考，一種從后往前思考，這里只講第一種思路：

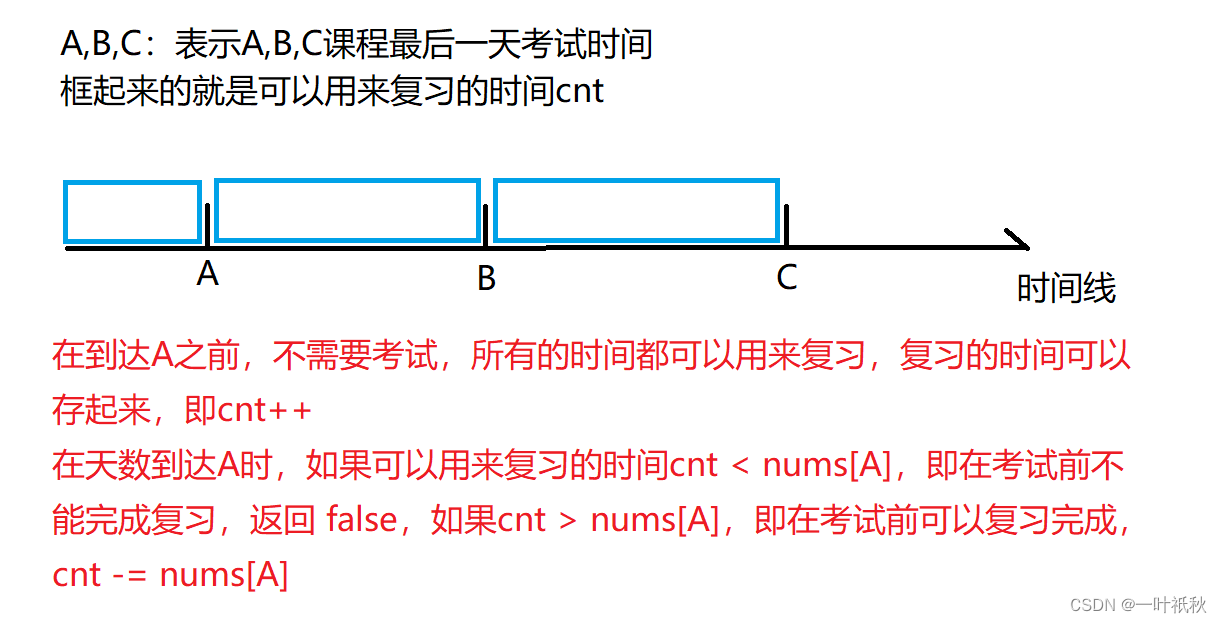
通過上面的分析，我們知道考試的時間越靠后，復習的時間就越多，就越能夠通過考試，所以我們需要求出每一門課程的最后一天考試時間，從前往后遍歷：

• 如果第 i 天不是某一門課程的最后一天考試天數，那么我們將這一天存起來（即cnt++），cnt 用作之后考試課程的復習天數
• 如果第 i 天是某一門課程的最后一天考試天數，那么先判斷我們是否有足夠的時間cnt去復習這門課程，如果有，cnt 減去需要復習的天數，如果沒有返回 false
• 遍歷結束返回 true

畫個圖理解一下：

?代碼如下：

class Solution {public int earliestSecondToMarkIndices(int[] nums, int[] changeIndices) {int n = nums.length;int m = changeIndices.length;int[] last_test = new int[n];int l = n, r = m;while(l <= r){int mid = (l + r) / 2;if(check(nums, changeIndices, last_test, mid)){r = mid - 1;}else{l = mid + 1;}}return r+1 > m ? -1 : r+1;}boolean check(int[] nums, int[] changeIndices, int[] last_test, int lastDay){Arrays.fill(last_test, -1);for(int i=0; i<lastDay; i++){//求每一門考試在規定時間(lastDay)內的最后的考試時間last_test[changeIndices[i]-1] = i;}for(int x : last_test){//在規定時間內沒有該課程的考試機會if(x < 0) return false;}int cnt = 0;for(int i=0; i<lastDay; i++){int idx = changeIndices[i]-1;//第i天的可以考試的課程if(last_test[idx]==i){if(cnt < nums[idx])return false;cnt -= nums[idx];}else{cnt++;}}return true;}
}

簡單講一下后往前遍歷的思路：和第一個思路一樣，只不過這里是透支復習的時間，也就是先考試，復習的天數先欠著，之后再還。（個人認為第一種更好理解，這種看不懂也沒事）

代碼如下：

class Solution {public int earliestSecondToMarkIndices(int[] nums, int[] changeIndices) {int n = nums.length;int m = changeIndices.length;if (n > m) return -1;int[] done = new int[n]; // 避免反復創建和初始化數組int left = n - 1, right = m + 1;while (left + 1 < right) {int mid = (left + right) / 2;if (check(nums, changeIndices, done, mid)) {right = mid;} else {left = mid;}}return right > m ? -1 : right;}private boolean check(int[] nums, int[] changeIndices, int[] done, int mx) {int exam = nums.length;int study = 0;for (int i = mx - 1; i >= 0 && study <= i + 1; i--) { // 確保剩余的天數>要復習的天數int idx = changeIndices[i] - 1;if (done[idx] != mx) {//判斷是否考過試done[idx] = mx;exam--; // 考試study += nums[idx]; // 需要復習的天數} else if (study > 0) {study--; // 復習}}return exam == 0 && study == 0; // 考完了并且復習完了}
}

四，3049. 標記所有下標的最早秒數 II

二分 + 反悔貪心

該題和上一題有兩個不一樣的地方：

1）可以在第 i 天，一天就復習完 changIndices[i] 這門課程（快速復習）

2）可以在任意一天考任意一門課程

這里有一個需要注意的點：快速復習和慢速復習（一天一天復習，復習nums[i]天）是沖突的，會造成浪費，也就是說，一門課程要么使用快速復習，要么使用慢速復習，可以使用反證法證明，當一門課程即使用快速復習，又使用慢速復習，就會浪費慢速復習的時間。

還有一個問題，快速復習的時間是越早越好還是越晚越好？這點可以從貪心的思路去想，復習完的時間越早，就有更加充足的時間去考試，所以答案是越早越好。統計所有課程最早的快速復習時間。

根據上一題來看，這道題是否也可以使用二分答案去做呢？這也是可以的，因為它的單調性還與上道題一樣：給的時間越多，復習的時間越充裕，越能夠通過考試。

如何判斷所給的天數是否充足，這道題只能從后往前遍歷，因為從前往后遍歷的話，無法知道是否有足夠的時間用來考試。

從后往前遍歷：

• 當天不是一門課程快速復習的最早時間，cnt += 1
• 當天是一門課程快速復習的最早時間：

1. cnt>0，即有時間去考試，那么消耗一天去考試，cnt-=1
2. nums[i]=0，即不需要時間復習，cnt+=1
3. nums[i]=1，可以通過慢速復習，cnt+=1
4. cnt=0，即沒有時間去考試，但是不意味著該門課程一定是慢速復習，可以通過反悔貪心，去看看有沒有原本使用快速復習，且nums[i]最小的課程，如果有，反悔這門課（快速復習一天+考試一天），多出來的這兩天，用來做當天這門課的快速復習+考試

最后看看剩下的使用慢速復習+考試的天數是否大于實際上的慢速復習+考試的天數

代碼如下：

class Solution {public int earliestSecondToMarkIndices(int[] nums, int[] changeIndices) {int n = nums.length;int m = changeIndices.length;if(n > m) return -1;long slow = n;for(int x : nums) slow += x;//統計慢速復習+考試需要多長時間int[] firstT = new int[n];//快速復習越早越好，這樣就可以留更多的時間去考試Arrays.fill(firstT, -1);for(int i=m-1; i>=0; i--)firstT[changeIndices[i]-1] = i;PriorityQueue<Integer> que = new PriorityQueue<>((a,b)->a-b);int l = n, r = m;while(l <= r){que.clear();int mid = (l+r)/2;if(check(nums, changeIndices, firstT, que, slow, mid)){r = mid - 1;}else{l = mid + 1;}}return r+1>m ? -1 : r+1;}boolean check(int[] nums, int[] changeIndices, int[] firstT, PriorityQueue<Integer> que, long slow, int lastDay){int cnt = 0;//表示有多少時間可以用來慢速復習+考試for(int i=lastDay-1; i>=0; i--){//從后向前遍歷int idx = changeIndices[i]-1;//當天可以快速復習的課程下標int x = nums[idx];//該課程需要幾天復習if(x <= 1 || i != firstT[idx]){//復習1天 || 不是最早的快速復習時間 -> 可以使用慢速復習搞定cnt++;//當天可以用來慢速復習/考試continue;}if(cnt == 0){//復習>1天 && 是最早的快速復習時間沒有慢速復習 && 沒有時間用來考試 -> 看看有沒有更節省的方式if(que.isEmpty() || x<=que.peek()){cnt++;//當天可以用來慢速復習/考試 即 該課程只能使用慢速復習continue;}slow += que.poll() + 1;//否則可以使que.poll()課程慢速復習+一天考試cnt += 2;//可以返還que.poll()課程所需的 1天快速復習 + 1天考試}slow -= x + 1;//減去當前課程復習天數+考試所需的一天cnt--;//當天快速復習 + 后面一天考試que.offer(x);}return cnt >= slow;//剩余留給慢速復習+考試的時間 > 實際所需慢速復習+考試的時間}
}