目錄

2368. 受限條件下可到達節點的數目

題目描述：

實現代碼與解析：

DFS

原理思路：

---

2368. 受限條件下可到達節點的數目

題目描述：

????????現有一棵由?n?個節點組成的無向樹，節點編號從?0?到?n - 1?，共有?n - 1?條邊。

給你一個二維整數數組?edges?，長度為?n - 1?，其中?edges[i] = [ai, bi]?表示樹中節點?ai?和?bi?之間存在一條邊。另給你一個整數數組?restricted?表示?受限?節點。

在不訪問受限節點的前提下，返回你可以從節點?0?到達的?最多?節點數目。

注意，節點?0?不?會標記為受限節點。

示例 1：

輸入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
輸出：4
解釋：上圖所示正是這棵樹。
在不訪問受限節點的前提下，只有節點 [0,1,2,3] 可以從節點 0 到達。

示例 2：

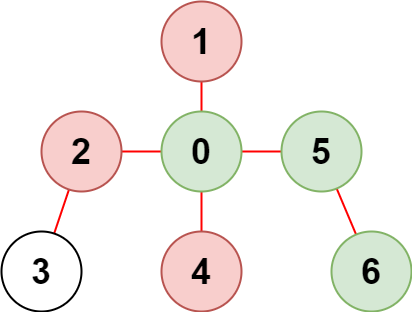
輸入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
輸出：3
解釋：上圖所示正是這棵樹。
在不訪問受限節點的前提下，只有節點 [0,5,6] 可以從節點 0 到達。

提示：

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges?表示一棵有效的樹
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted?中的所有值?互不相同

實現代碼與解析：

DFS

class Solution {public final int N = (int)2e5 + 10;// 鄰接表int[] h = new int[N], e = new int[N * 2], ne = new int[N * 2];int idx;// 連邊方法public void add(int a, int b) {e[idx] = b; ne[idx] = h[a]; h[a] = idx++;} public int reachableNodes(int n, int[][] edges, int[] restricted) {Arrays.fill(h, -1); // 別忘了// 構成鄰接表for (int[] e: edges) {int a = e[0];int b = e[1];add(a, b);add(b, a);}// set記錄被標記的節點Set<Integer> set = new HashSet<>();for (int t: restricted) {set.add(t);}// 從0節點dfs遍歷int res = dfs(0, -1, set);return res;}public int dfs(int cur, int f, Set<Integer> set) {int count = 0;for (int i = h[cur]; i != -1; i = ne[i]) {int j = e[i];if (j != f && !set.contains(j)) {count += dfs(j, cur, set);}}count++;return count;}
}

原理思路：

? ? ? ? 簡單的dfs，從0開始遍歷即可，統計可以走到的節點的個數。set用于記錄受限制的節點，作為遞歸條件。