總結

19-卷積層

【補充】看評論區建議的卷積動畫視頻

數學中的卷積

【鏈接】https://www.bilibili.com/video/BV1VV411478E/?from=search&seid=1725700777641154181&vd_source=e81e116c4ffe5e79d4bc44738263eda4

【可判斷是否為卷積的典型標志】兩個函數中自變量相加是否可以消掉，如 下面的τ + x-τ = x

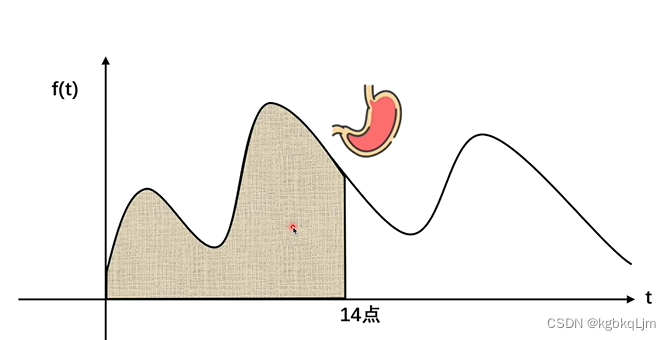
問在某一時刻 這個人的肚子中還有多少食物沒消化：
f(t)：進食的時間與進食的多少
g(t)：某個吃進去的食物 剩余的比例

當不考慮用戶消化食物時，下午兩點時用戶所剩食物就是f(t)的積分

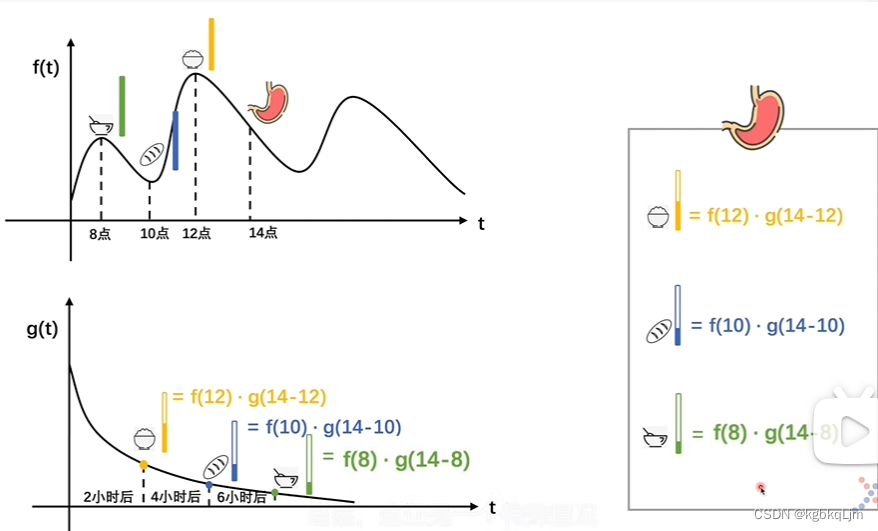
推廣到一般情況：

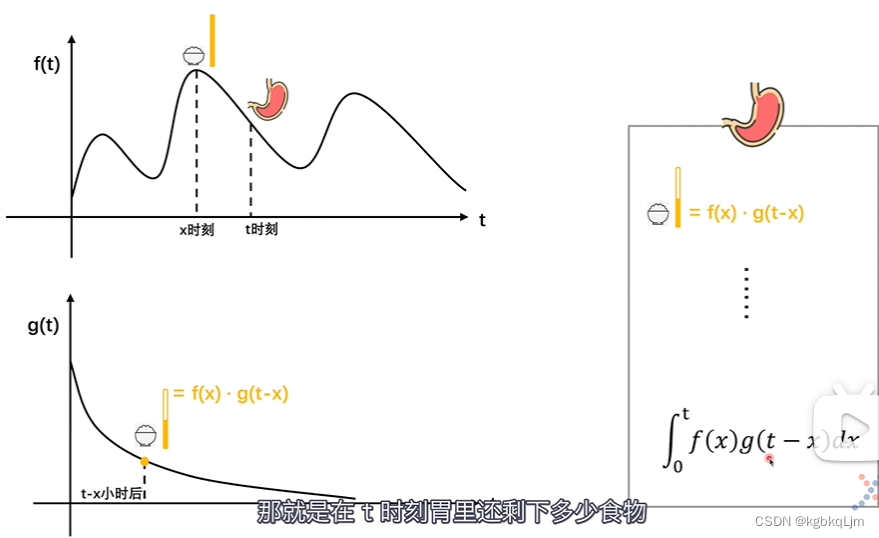
f(t)和g(t)中點的對應關系：

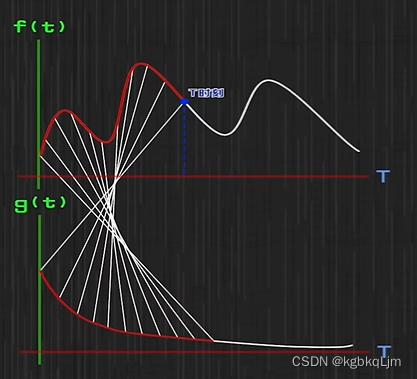
為什么叫卷積： g函數被翻轉了一下

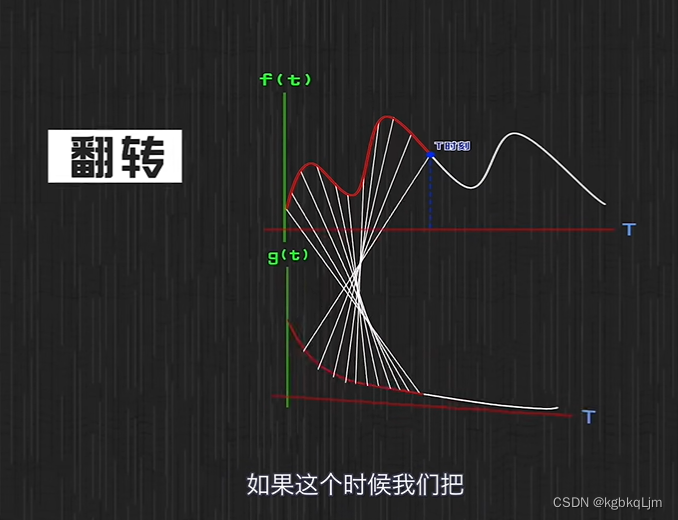
翻轉后：

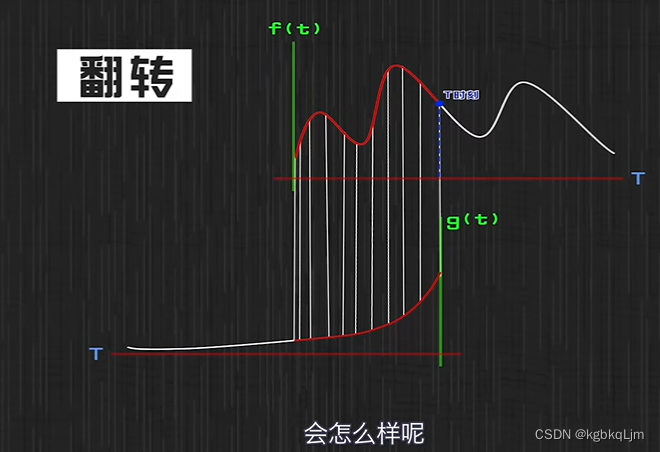
卷積神經網絡

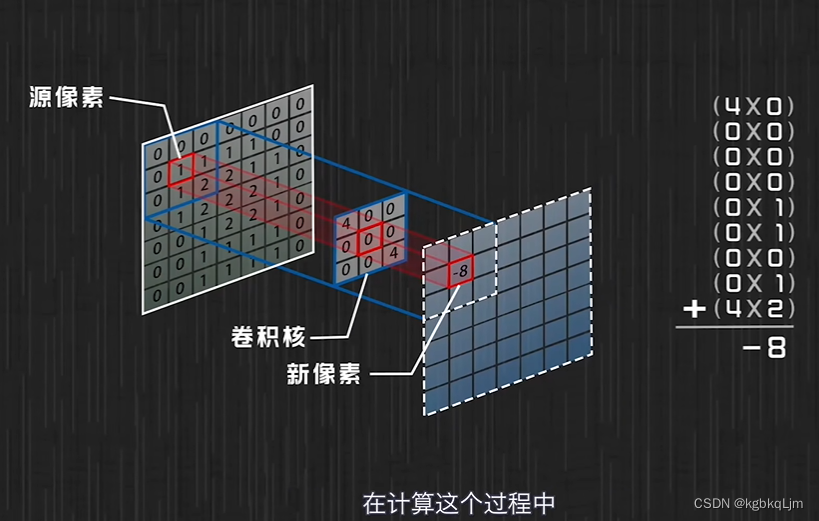
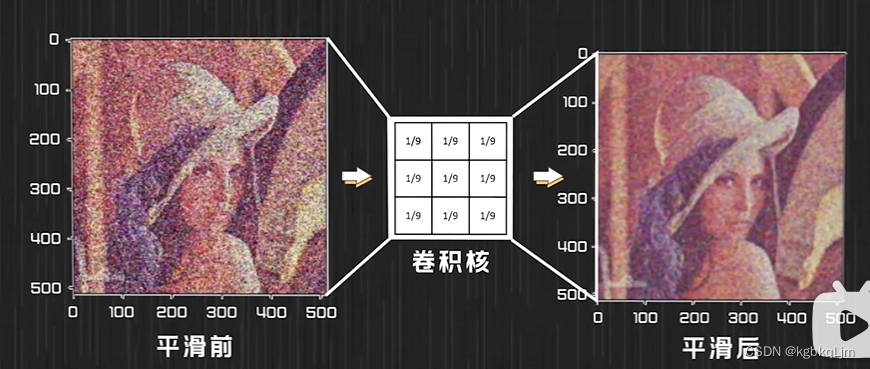
【舉例】卷積處理圖片后的效果

【卷積共有三層含義】

卷積核：過濾器，選擇不同的卷積核可以提到不同的局部特征
【卷積核參數設置】
不想考慮某個位置時，卷積核某位置設為0；想重點考慮某位置時，將卷積核某位置數值設置比較高

1.求均值的卷積核

【符號】
*即卷積
Σ連加：因為 考慮的是像素點，是離散的，因此不用積分用 Σ累加
g函數相當于規定了 周圍像素點如何對當前像素點產生的影響

下圖看到，對應關系還是有點擰著的


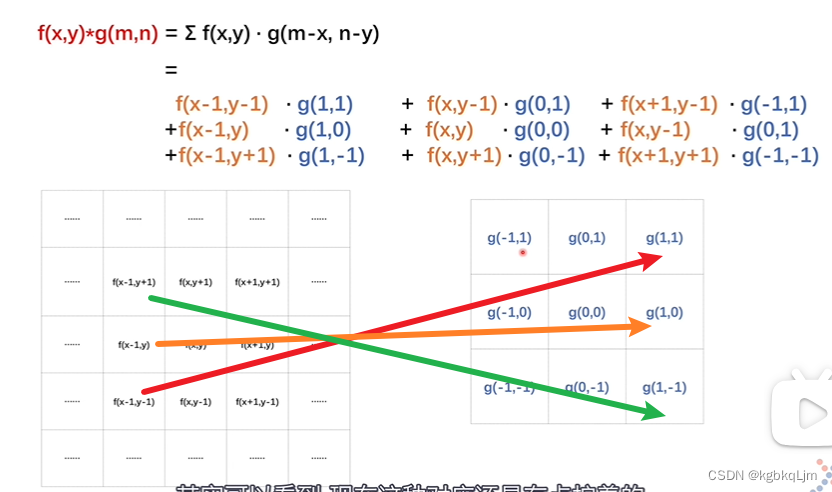
g函數旋轉180°后才是卷積核

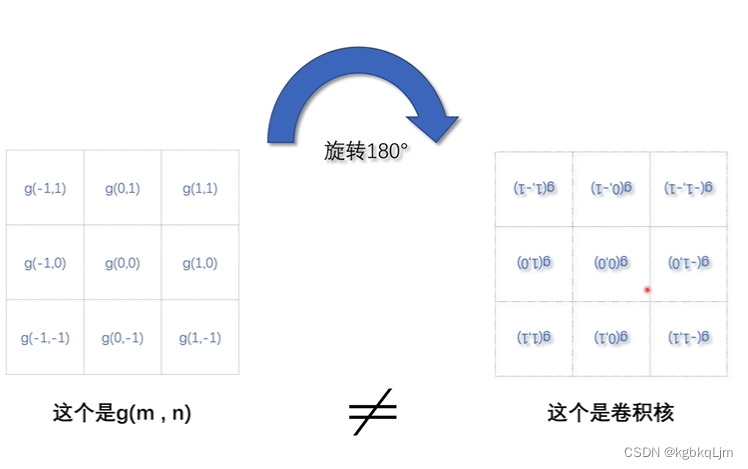
卷積核可以扣在圖像上進行對應相乘并最后相加（其實省略了旋轉這個步驟，但本質上仍然是卷積運算）

【局部性】看全局時，兩個圖片像素點不同，但是分別看局部，特征是一樣的

當只看局部時

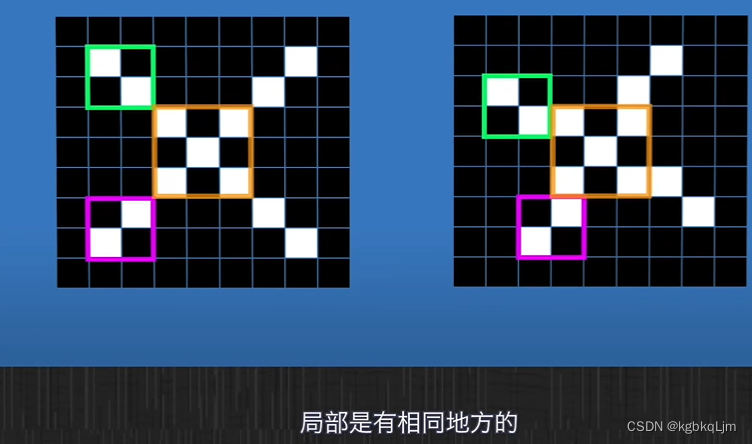
【不同的卷積核提取后的效果】

卷積（操作子）（從全連接到卷積）

下圖說明了 為什么卷積層是特殊的全連接層：
首先將原全連接層的權重w改寫為 四維的（即含二維輸入和二維輸出）i、j、a、b，
1.【平移不變性】然后對v進行一下重新索引（為保證其平移不變性） 丟掉i、j維度 （即在其他不關注的維度都是一樣的東西）后 為v_a,b；
2.【局部性】然后 限制a、b在 負derta~derta的范圍內（即只關注 某個位置i、j像素點 附近的東西）

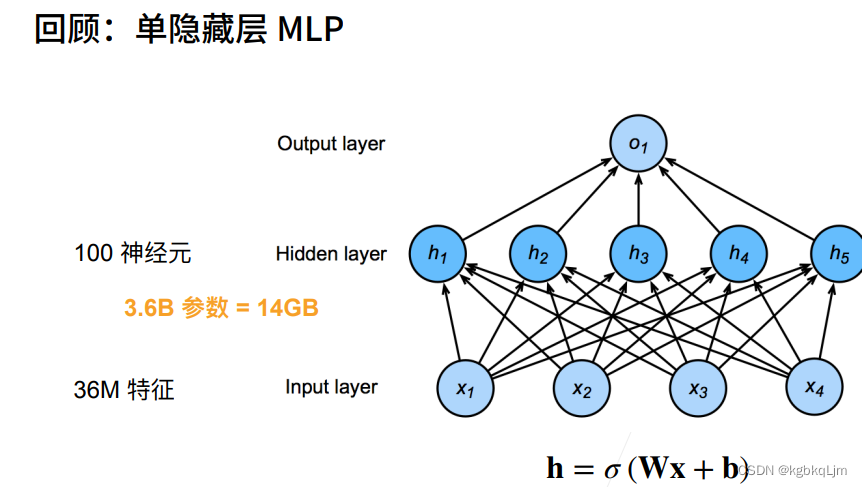
【引言】MLP處理圖片分類任務存在的問題

如一個12M（即1200萬）的彩色圖片 有RGB三通道，則共 36M像素（每個像素點有一個值），用單隱藏層訓練，在模型共有36億個元素，遠遠多余所有的貓狗的數量，這樣還不如直接記住所有種類

在圖片中找物體的兩個原則

【兩個原則】
1.平移不變性：圖片識別分類器在識別物體時不會因為該物體像素在圖片中出現位置的不同 而改變識別結果（待識別物體出現在圖片中任何位置時，應該都能準確識別才行）

2.局部性：只需要看局部信息即可，不需要看全部信息

這兩個原則也啟發了后續的設計

下面從全連接層出發，應用卷積（即特殊的全連接層）

重新考察全連接層

【此處用矩陣的原因】之前用全連接層時，就將二維矩陣轉換成了一維向量，但此時要考察一些空間信息，因此需要用矩陣來計算。

【為何reshape為4D tensor】輸入和輸出都變成了二維的，權重表示使用下標，要顯示輸入輸出的高寬，所以權重就是四維的

參數解釋：（搜一下卷積的動圖，原來全連接層是一個權重，現在是一個矩陣的權重）
h_i,j：輸出（之前學習的全連接層時 是 h_i）
w_i,j,k,l：權重（之前是二維，現在是四維）（之前得輸入層和隱藏層是向量，所以w下標為兩個。現在輸入層和隱藏層變成矩陣，所以w下標是四個。）
x_k,l：輸入（之前學習的全連接層時是 x_i）
（彈幕）Wijkl里面的kl是對應X的kl也就是輸入的矩陣的元素，ij代表卷積核里面和kl相乘的那個值，因為卷積核的值不會變但是會滑動所以sigma下標是kl，實際就是滑動卷積的意思

【w下標的變換得到v】然后對w進行重新索引（即 重新排列），得到v， 因此 也會使得x的下標有點變化

平移不變性

【從圖像卷積角度理解， 用卷積核去掃input圖像時，卷積核的內容是不變的】
【i、j是位置，i+a、j+b是 以ij位置為參照點進行平移后得到的位置】

至此存在的問題：輸入x的平移會導致v的平移（如 x 的i、j分別平移為i+a、j+b，則 識別圖像的權重 v也會隨之變化），但我們的目標是 x的變化不應該引起v的變化

【權重就是特征提取器，不應該隨位置而發生變化】i、j應該是 圖片中不同的位置索引，將v改為v_a,b后（即丟掉v的i、j兩個維度），就不依賴于 輸入x的位置i、j了

雖然下圖紅框是二維卷積，但是嚴格在數學上來說是 二維交叉相關

局部性

【從圖像卷積角度理解， 用卷積核去掃input圖像時，每次只關注input圖像中 卷積核掃描的那一部分，而不是每次關注全部input圖像】
理論上，以i、j為中心，可以平移到任意位置，但實際上 我們不應該看離i、j太遠的位置（即令太遠的v_a,b=0，即不關注了），應該只看其附近的點
即：關注的位置 即 i、j變化的位置i+a、j+b 只關注 a和b在 [-derta，+derta]的范圍內（即下圖橙框）

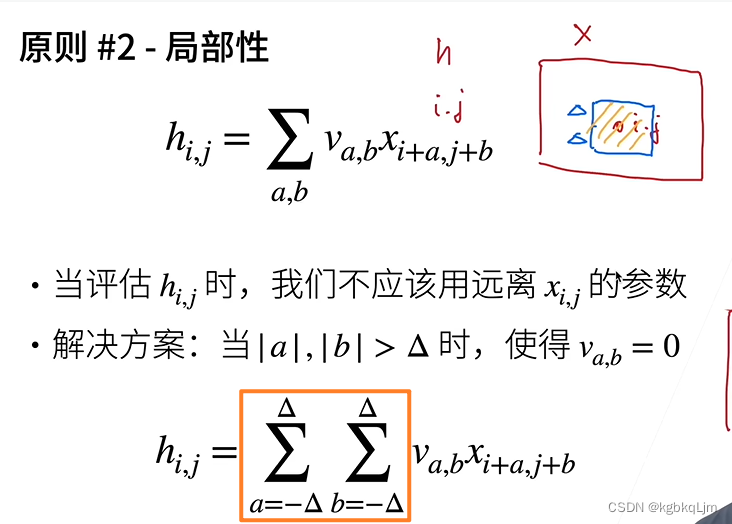
【局部性-補充】評論區推薦視頻的通俗理解：
看全局時，兩個圖片像素點不同，但是分別看局部，特征是一樣的

當只看局部時

卷積層

核矩陣（即卷積核）W和偏移b都是可以學習的參數
核矩陣（卷積核）的大小是超參數，其控制局部性

概述

二維卷積

全程中 核是不變的（即平移不變形）

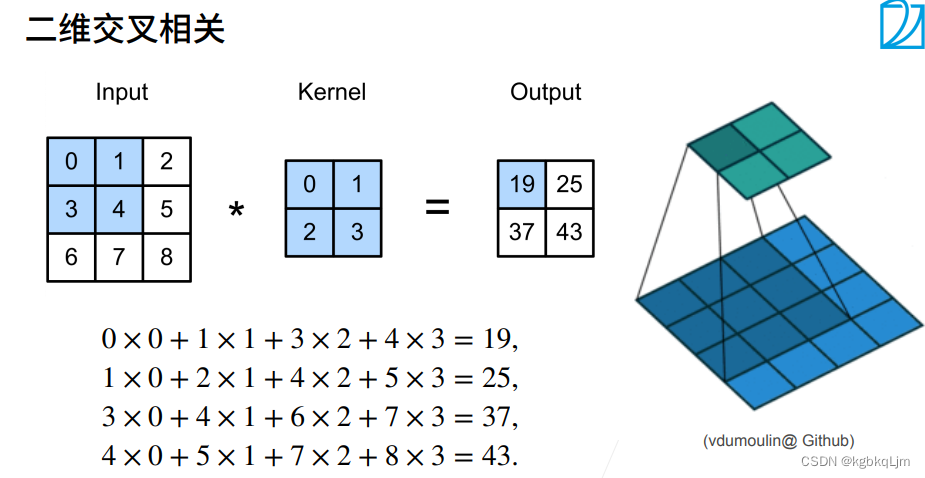
【二維卷積層】
用卷積核去掃描時，丟掉的內容就是 (kh - 1) x （kw - 1）
下圖中 五角星 即為 上節定義的二維交叉相關操作子；
W和b都是可以學習的參數

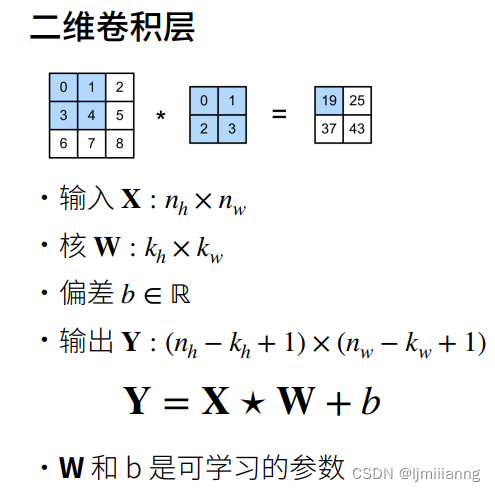
【舉例】
彈幕說：卷積核肯定是自己學，因為卷積核中每個元素都代表一個weight

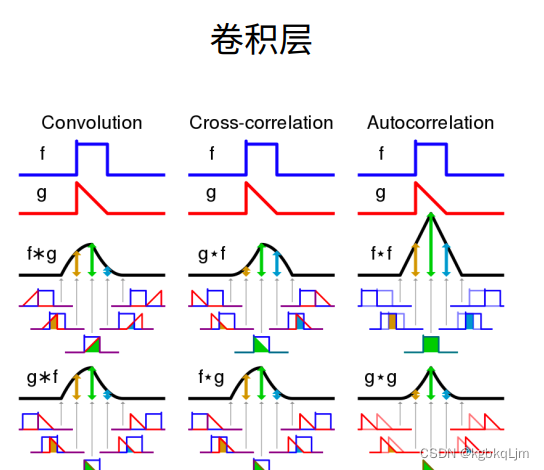
交叉相關

交叉相關和卷積沒有太多區別，唯一的區別是w角標中的a、b和-a、-b
（彈幕說：是不是說卷積時他的核需要逆時針旋轉180°，相關不需要。
實際運算時反正參數推出來了，效果也達到了，所以我們就不去深究里面翻轉前后代表的意義了）

實際應用中雖然說 使用的是卷積操作，但是實際上用的是交叉相關（因為 嚴格來說卷積 要按照下圖中這么寫，即 w角標為-a、-b，但 我們 從使用者的角度 并不嚴格）

一維和三維交叉相關

主要關注的還是二維圖像

代碼

互相關運算

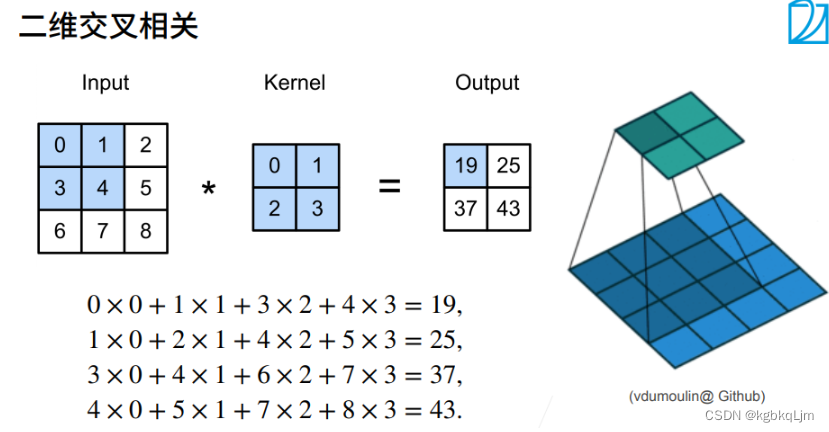
# 互相關運算
import torch
from torch import nn
from d2l import torch as d2ldef corr2d(X, K):   # X 為輸入，K為核矩陣"""計算二維互相關信息"""h, w = K.shape  # 核矩陣的行數和列數Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # 初始化輸出Y的形狀。X.shape[0]為輸入高    for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i, j] = (X[i:i + h, j:j + w] * K).sum() # 圖片的小方塊區域與卷積核做點積return Y# 驗證上述二維互相關運算的輸出
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
K = torch.tensor([[0.0,1.0],[2.0,3.0]])
corr2d(X,K)

二維卷積層

互相關運算，就是類似于點積，對應位置（卷積核覆蓋的區域）元素相乘再相加，

【應用】檢測圖像顏色邊緣

對于某一個圖像，如果 某個像素與其相鄰像素相同，則 與 [1,-1]核運算后 為0，則不是邊緣； 如果某處是邊緣（即 由0變為1或1變為0），則 與[1,-1]核運算后 不為0（要么是1，要么是-1）

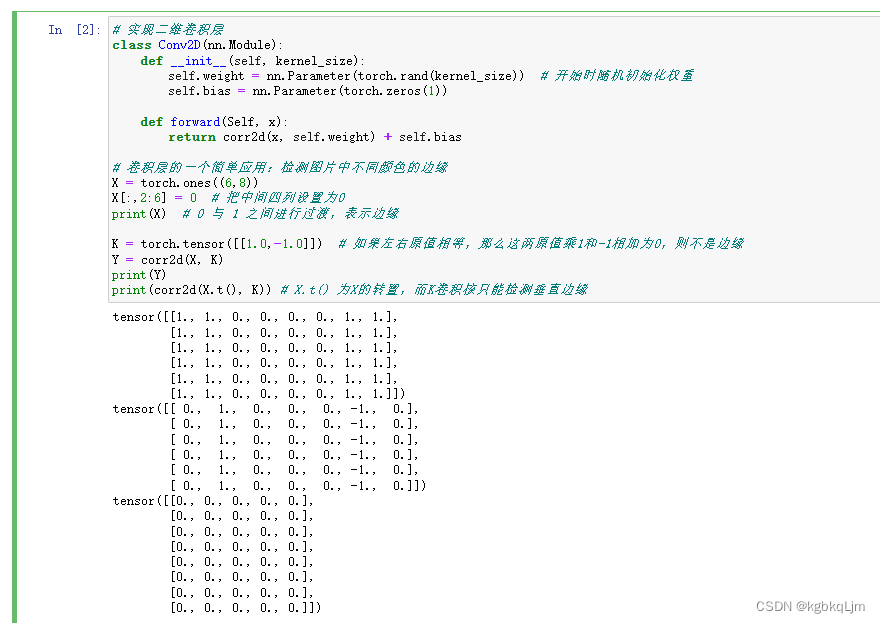
# 實現二維卷積層
class Conv2D(nn.Module):def __init__(self, kernel_size):self.weight = nn.Parameter(torch.rand(kernel_size))  # 開始時隨機初始化權重self.bias = nn.Parameter(torch.zeros(1))def forward(Self, x):return corr2d(x, self.weight) + self.bias# 卷積層的一個簡單應用：檢測圖片中不同顏色的邊緣
X = torch.ones((6,8))
X[:,2:6] = 0  # 把中間四列設置為0
print(X)  # 0 與 1 之間進行過渡，表示邊緣K = torch.tensor([[1.0,-1.0]])  # 如果左右原值相等，那么這兩原值乘1和-1相加為0，則不是邊緣
Y = corr2d(X, K)
print(Y)
print(corr2d(X.t(), K)) # X.t() 為X的轉置，而K卷積核只能檢測垂直邊緣

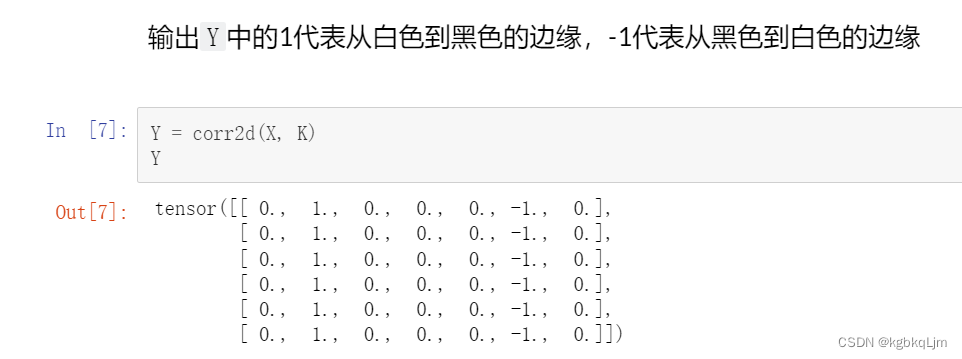
給定輸入X和輸出Y，學習得到卷積核K

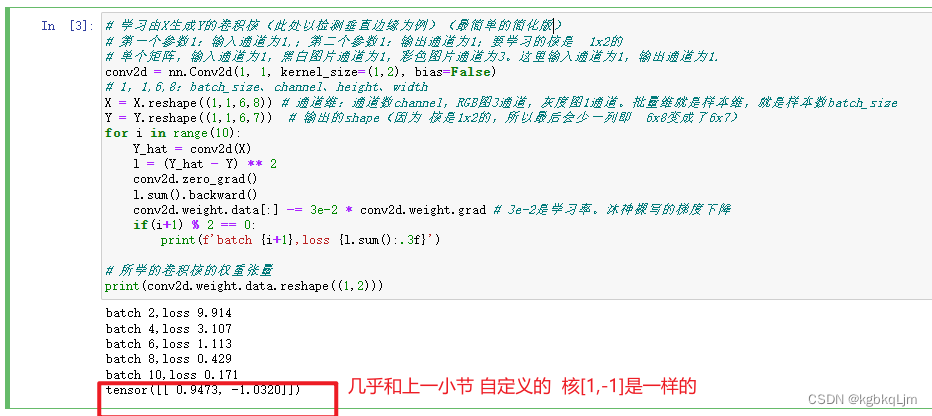
# 學習由X生成Y的卷積核（此處以檢測垂直邊緣為例）（最簡單的簡化版）
# 第一個參數1：輸入通道為1,；第二個參數1：輸出通道為1；要學習的核是  1x2的
# 單個矩陣，輸入通道為1，黑白圖片通道為1，彩色圖片通道為3。這里輸入通道為1，輸出通道為1.   
conv2d = nn.Conv2d(1, 1, kernel_size=(1,2), bias=False) 
# 1，1,6,8：batch_size、channel、height、width
X = X.reshape((1,1,6,8)) # 通道維：通道數channel，RGB圖3通道，灰度圖1通道。批量維就是樣本維，就是樣本數batch_size
Y = Y.reshape((1,1,6,7))  # 輸出的shape（因為 核是1x2的，所以最后會少一列即  6x8變成了6x7）
for i in range(10):Y_hat = conv2d(X)l = (Y_hat - Y) ** 2conv2d.zero_grad()l.sum().backward()conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad # 3e-2是學習率。沐神裸寫的梯度下降if(i+1) % 2 == 0:print(f'batch {i+1},loss {l.sum():.3f}')# 所學的卷積核的權重張量
print(conv2d.weight.data.reshape((1,2)))

QA

17.沒區別。
100個神經元的單隱藏層MLP 即有 一個輸出維度為100的全連接層

只是為了說明 為什么卷積是特殊的全連接層

19.圖片輸入時就是一個二維的（就是個矩陣）
之前使用softmax回歸時，把圖片reshape成了一個一維向量

20.沒聽過

21.感受野即kernel的大小

這個問題類似于之前全連接層提到過的 一個很淺的很寬的全連接層的效果沒有 一個 深一點且窄一點的全連接層效果好
同理對于卷積層，使用層數少且每層核大 的 效果不如 層數多且每層的核小一點 的效果好

一般用3x3或5x5

這個就是inception的設計思路

23.信號與處理中 就是那么定義的，深度學習只是拿來用用，并沒糾結細節

24.不管在圖片的哪個位置，核是不變的

25.只是為了講課定義的

26.數字信號處理中 可以看看

27.抖動厲害的原因：（抖動沒事，只要 呈下降趨勢即可，但是一直抖不下降是有問題的）
（1）數據多樣性很大，每次隨機采樣的數據 區別很大， 這樣是沒事的（ 可以做平滑，好看一點）
（2）學習率很大。可以降低學習率lr （或者batch_size大一點）

不是這個意思。

全連接層最大的問題是 權重矩陣W的高（好像就是 矩陣的行數）取決于 輸入的寬 。那么此時當給定的輸入是 1200萬像素的圖片，那么 輸入維度就是1200萬，那么權重矩陣參數量太大 就炸掉了。
而 卷積不存在這種問題，因為卷積核大小是固定的，無論輸入的大小是多大（而且實際上也不會直接丟進去一個 1200萬像素的輸入）

彈幕說：mlp放不下的原因是因為權重參數的矩陣過大

20-卷積層中的填充和步幅

填充和步幅

卷積核大小kernel_size、填充padding、步幅stride都是 超參數

博客：
① 奇數卷積核更容易做padding。我們假設卷積核大小為k * k，為了讓卷積后的圖像大小與原圖一樣大，根據公式可得到padding=（k-1）/2，這里的k只有在取奇數的時候，padding才能是整數，否則padding不好進行圖片填充。

② k為偶數時，p為浮點數，所做的操作為一個為向上取整，填充，一個為向下取整，填充。

填充padding

【總結】通常情況下，padding的高寬是對稱的，且取為核大小-1，即ph=kh-1、pw=kw-1（這個是指課件理論中的 含上下或左右的 某個方向一共填充的大小，如果 在代碼中 要寫為 padding=ph/2）。從而使得輸出形狀=輸入形狀
【注意ph、pw與代碼中的padding】此處填充ph和pw是指 從高度方向、寬度方向 共填充了多少，如 ph=2 上下共填充了2行，相當于 代碼中的padding=1。即 對于 卷積核大小為3x3的、padding=1（代碼中寫padding=1，課件理論中ph、pw=2，二者是二倍的關系） 進行卷積操作后，輸入和輸出形狀相同；對于 5x5的卷積核大小、padding=2（代碼中寫padding=2，課件理論中ph、pw=4），輸入和輸出形狀相同

nh和nw為輸入數據的高、寬

【引言-填充】當不使用padding時，經過多層卷積后 形狀會變得很小

下圖中：每一層都會減4，第七層大小就變成4X4了

【正文-填充】

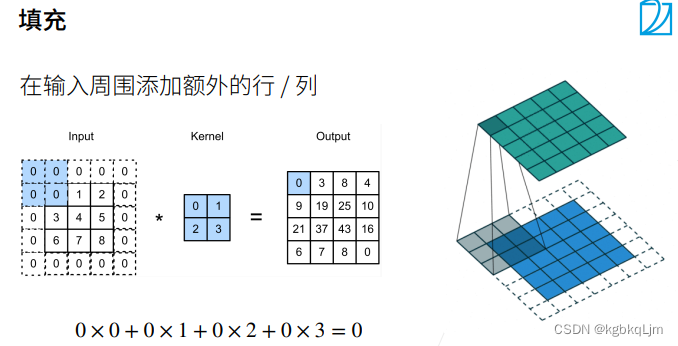
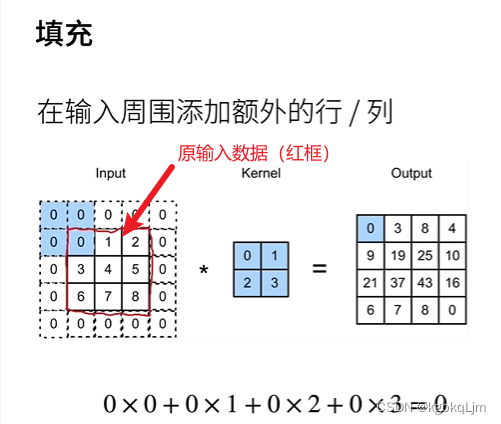
【有填充時的輸出形狀計算】
【注意ph、pw與代碼中的padding】此處填充ph和pw是指 從高度方向、寬度方向 共填充了多少，如 ph=2 上下共填充了2行，相當于 代碼中的padding=1。即 對于 卷積核大小為3x3的、padding=1 進行卷積操作后，輸入和輸出形狀相同；對于 5x5的卷積核大小、padding=2，輸入和輸出形狀相同

p為padding，當 按下圖中通常方式取ph和pw（即ph=kh-1、pw=kw-1）時，無論核的大小如何，輸出和輸入的形狀相同
一般來說很少用核長寬為偶數的卷積核
下圖中的類似[ ] 的是向上、下取整

步幅stride

【引言-步幅】

【正文-步幅】每次移動核時，可以 一次向右和向下 移動幾格
下圖中第一個圖的兩個藍色區域是 分別從 起點（即左上角）向右移動一次（2步幅）、向下移動一次（3步幅）。
當繼續移動 剩余區域不夠時，就不移動了

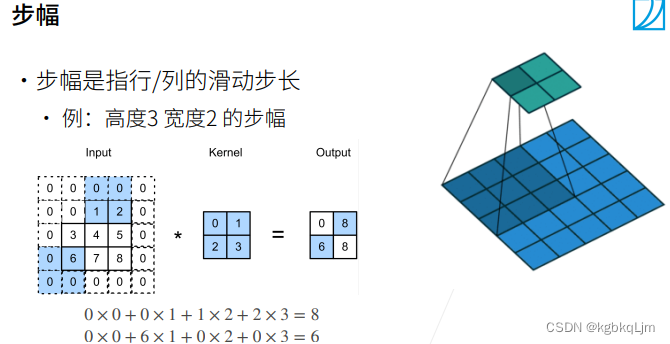
【有步幅時的輸出形狀計算】
根據公式，如果 stride=2，那么 輸出尺寸的高寬相當于減半

類似中括號的是 floor向下取整

代碼

【通常情況下都是對稱的】輸入的數據形狀是 高寬相同的，padding是對稱的，stride也是對稱的

【注意ph、pw與代碼中的padding】此處填充ph和pw是指 從高度方向、寬度方向 共填充了多少，如 ph=2 上下共填充了2行，相當于 代碼中的padding=1。即 對于 卷積核大小為3x3的、padding=1 進行卷積操作后，輸入和輸出形狀相同

# 在所有側邊填充1個像素
import torch
from torch import nndef comp_conv2d(conv2d, X): # conv2d 作為傳參傳進去，在內部使用# 在維度前面加入一個批量大小數batch_size和通道數channel（因為暫時沒考慮批量大小數和通道數）X = X.reshape((1,1)+X.shape) Y = conv2d(X)  # 卷積處理是一個四維的矩陣return Y.reshape(Y.shape[2:]) # 將前面兩個維度拿掉# 【填充】在所有側邊分別填充1個像素
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1) # padding=1 為左右都填充一行，相當于之前講的ph、pw=2
X = torch.rand(size=(8,8))
print(comp_conv2d(conv2d,X).shape)  # torch.Size([8, 8])  即沒改變輸入的形狀
# 【填充】填充不同的高度和寬度（核的形狀為5x3, 填充時上下分別填充2行、左右分別填充1列）
conv2d = nn.Conv2d(1,1,kernel_size=(5,3),padding=(2,1))
print(comp_conv2d(conv2d,X).shape)  # torch.Size([8, 8])  即沒改變輸入的形狀# 【填充+步幅】將高度和寬度的步幅設置為2
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2)
print(comp_conv2d(conv2d,X).shape)   # torch.Size([4, 4])。
# 因為步幅sh、sw為2，可以被輸入的高、寬整除，因此輸出為(nh/sh） x （nw/sw)# 【填充+步幅】一個稍微復雜的例子
conv2d = nn.Conv2d(1,1,kernel_size=(3,5),padding=(0,1),stride=(3,4))
print(comp_conv2d(conv2d,X).shape)  # torch.Size([2, 2])  。 套公式計算

QA

1. ppt錯了，55層

重要程度：核大小> 填充通常取默認的、步幅取值取決于你要把你的模型大小控制在什么程度
卷積核大小kernel_size：
填充padding：通常ph和pw取值為 卷積核大小-1 ，從而實現 卷積核不改變輸入形狀大小（注意 如果是代碼中 padding=1 相當于課件中的ph、pw=2）
步幅stride：通常padding=1（因為如果每層都減半，經過幾個卷積層后 圖片就很小 幾乎沒了 這樣就 做不了深的神經網絡了，因此減半是個別情況）。 不為1時 是因為計算量太大了，此時通常步幅取2。步幅越大，計算量越小；步幅越小，模型所需層數就很大（因為一般是 想將一個很大的輸入圖片 變成一個很小的）

3.是的。因為padding（課件理論中）=kernel-1，而padding是分在圖片上下的，kernel為基數，padding就可以對半分。
注意 課件理論中的 ph、pw 除以2才為代碼中的 padding

當然，也可以取偶數

4.看第二個問題
減半是很少的情況，大多數情況是不變的

padding、stride、通道數，這些是神經網絡架構設計的一部分，當用不同的神經網絡時 一般都會告訴你這些參數如何設定

6.一般來說很少會自己純手寫神經網絡， 如用ResNet（kaiming大神的殘差神經網絡）就夠了，其也分很多系列。除非你的輸入是非常不一樣的情況，如 是20x1000，很扁的這種，可能需要自己設計神經網絡，否則一般用經典的即可 或 在經典的基礎上做調整。

即便自己設計神經網絡，也是參照經典神經網絡的基礎上

7.回看代碼

8.回看代碼

9.不存在這種情況

雖然單獨看3x3很小，但是 如果神經網絡很深時， 較深的層中的每個元素 能看到 足夠大的圖片信息

高層會看到低層所看到信息總和
對于后面比較深的卷積層中的 1x1、3x3這種，其實 每個元素對應的是 較淺層中很大的圖片范圍的，看到的信息并不小

11.NAS（Neural Network Architecture Search），也是自動機器學習的一部分
彈幕說：autodl和automl，計算成本太高，不是一般人研究的起的

（1）方式一：設計很多神經網絡結構，從中選擇效果最好的

12.從信息論的角度來說，特征信息肯定會丟失的
ML本質是一個極端的壓縮算法：給你一個圖片，最后得到一個類別、有語義信息的數值。 即把 比較原始的計算機能理解的像素信息、文字字符串的信息壓縮到人能理解的 語義空間中

13.有，但是成本極大（沐神的一個實驗跑了100w美金）

14.同13

15.是可以人為控制的

16.從理論上來說，大概是：三個3x3卷積核的效果是可以用2個5x5卷積核來替代的；10層3x3卷積的效果可以等效成5或6層 的5x5的卷積，
但是，3x3卷積更快，（涉及計算復雜度、成本方面的問題、更“貴”）

17.可以這樣用。但是一般來說，簡單高效易懂的更容易被人記住，即類似 都用比較簡單的核。
太復雜的 可以不容易被人理解

18.后面會講，不同的卷積層 可以看不同的紋理特征

DL不是有錢人的游戲。
如果不用DL：
1、用人，機器成本可能會低點，可能效果差，就需要更多的調參，即人力成本。
2、其次數據成本很大，數據很貴

DL使用GPU的算力來替代 人力成本和數據成本， 雖然計算算力變高。
NAS現在是有錢人的游戲，但是任何科技都是從很貴到很便宜的過程（如當年的磁盤計算機也很貴）

21-卷積層里的多輸入和多輸出

輸出通道是當前卷積層的超參數， 輸入通道是 上一個卷積層的 超參數（即上一個卷積層的輸出通道）

多輸入輸出通道

引言

之前Fashion mnist是單通道（只有一個灰）

正文-多個輸入通道

【多個輸入通道】
如下圖，通道0的數據和通道0的卷積核做點積運算，同理通道1，最后將兩個通道的結果相加

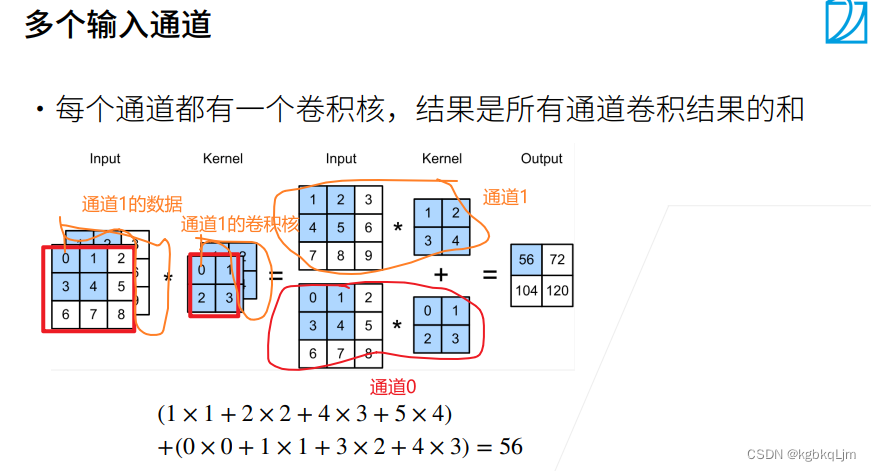
現在假定輸入數據X是三維的tensor，即三個通道，則卷積核也變成了三維的（與輸入數據維度相同）；每個通道都有一個 偏移（即長為c_i的向量），此處只是沒寫
i：input
輸出是單通道的，因為不管輸入有多少個通道，都是最后按通道相加

正文-多個輸出通道

【多個輸出通道】 多個輸入通道和多個輸出通道其實是沒有相關性的，可以分別設置
【個人理解，暫時沒問題】輸出通道數=卷積核個數，即下圖中co

對于每個輸出的通道，都有一個自己的三維卷積核，
c_o：output channel

彈幕說：這里等于就是利用多個卷積核，分別對輸入進行上一頁PPT的卷積操作，最后將結果分通道疊在一起。ci個通道，每個通道co種卷積核，共有ci*co種卷積核。

老師說：對每一個輸入（下圖中第一個紅框），把它對應的一個輸出通道的核拿出來（第二個紅框），就會得到一個對應的輸出通道（第三個紅框），對每一個輸出通道一一這樣運算，最后將結果concat起來，得到輸出Y

Y_i,:,:輸出里面的第i個通道

【多個輸入和多個輸出通道的意義】
多輸出通道：每個輸出通道可以取識別一種模式（如不同的卷積核 可以提取不同 角度的特征，如 邊緣、銳化、顏色、紋理等），通過學習不同的卷積核權重 來匹配不同的模式，如下圖中有6個輸出通道

多輸入通道：假設將上一層 得到的六個輸出通道的結果 丟給下一層，將每個通道的到的結果組合起來（如 加權相加），得到組合的模式識別。這是對于相鄰的兩層，從整體的深度網絡來看，淺層、下面的層識別 具體細節特征如 邊緣特征、紋理等，
深層次的層可以將之前淺層得到的 分別的特征（模式）進行組合（如 將 胡須、眼睛等 組合起來 得到一個貓頭，最深層、最高層 可能得到一整只貓）

1x1卷積層

【1x1卷積層可以認為是卷積層，也可以等價認為是一個全連接層】
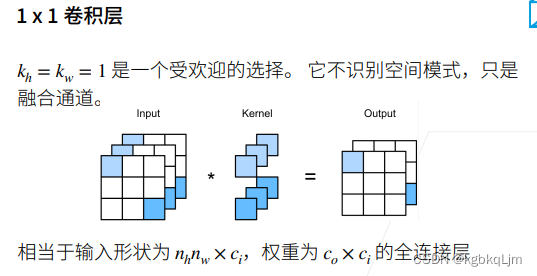
【作用】不識別空間模式，只是融合通道（對每個像素所對應的通道的向量 做一個全連接層，然后該全連接層對每個像素分別作用一遍）（Conv 1×1 一般只改變輸出通道數，而不改變輸出的寬度和高度；而Pooling 操作一般只改變輸出的寬和高，而不改變通道數）
卷積核的高寬均為1，每次只看一個像素（即不看 周圍空間的特征，即其不識別空間信息，不看當前這個像素與周圍其他像素的關系）
本質上等價于一個 形狀為n_hn_w x c_i、權重為c_o x c_i x 1 x 1的全連接層

輸出為0的通道，輸出為1的通道

彈幕說：
1.其實就是對input里的3個矩陣做全連接，這里是做了兩次不同權重的全連接
2. 3個輸入通道經過一個核得到一個輸出通道，這里有兩個核，所以得到兩個輸出通道
3. 對的，這里理解為兩組核或者兩套核比較好一些，一組核包括三個核

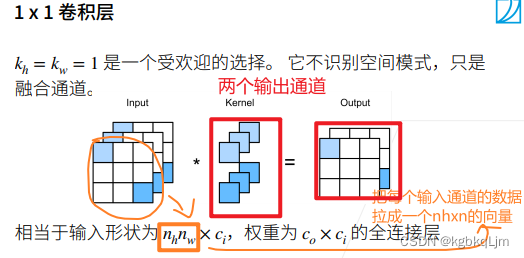
最通用情況下的二維卷積層

【偏差B的理解（彈幕說）】
每一個卷積核都對應一個單獨的偏差
pytorch的官方文檔，bias是和卷積核個數相同
其實就是Co組核，每組核有Ci個偏差
這里+B是用了廣播機制（不確定）

【計算復雜度的理解】
可以這么理解，輸出層共有CoMhMw個元素，每個元素都是size大小為CiKhKw的卷積核計算得到的

代碼

多輸入通道互相關計算

【zip的作用】
彈幕：
zip(X, K)函數可以將X和K的每個通道配對，返回一個可迭代對象，其中每個元素是一個(x, k)的元組，表示一個輸入通道和一個卷積核。
zip函數用于將可迭代的對象作為參數，將對象中對應的元素打包成一個個元組，然后返回由這些元組組成的列表。

多輸出通道的互相關計算

torch.stack():沿著一個新維度對輸入張量序列進行連接，序列中所有的張量都應該為相同形狀
下圖中即在dim=0這個維度上 進行堆疊

三個卷積核，每個卷積核有兩個通道，每個通道是2*2的矩陣

# 多輸入通道互相關運算
import torch
from d2l import torch as d2l
from torch import nn# 多通道輸入時的互相關運算
def corr2d_multi_in(X,K):  # 此處假設X和K都是3D的return sum(d2l.corr2d(x,k) for x,k in zip(X,K)) # X,K為3通道矩陣，for使得對最外面通道進行遍歷
# zip(X, K)函數可以將X和K的每個通道配對，返回一個可迭代對象，其中每個元素是一個(x, k)的元組，表示一個輸入通道和一個卷積核。X = torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])
K = torch.tensor([[[0.0,1.0],[2.0,3.0]],[[1.0,2.0],[3.0,4.0]]])
print(corr2d_multi_in(X,K))# 多輸出通道運算
def corr2d_multi_in_out(X,K):  # X為3通道矩陣；K為4通道矩陣，最外面維為輸出通道      # 彈幕說：就是從4D的K中拿出一個3D的k進行上一步操作# 大K中每個小k是一個3D的Tensor。0表示stack堆疊函數里面在0這個維度堆疊。           return torch.stack([corr2d_multi_in(X,k) for k in K],0) print(K.shape)
print((K+1).shape)
print((K+2).shape)
print("K:",K)
print(K+1)
K = torch.stack((K, K+1, K+2),0) # 原來的K是3D的，現在使用stack創建一個 三輸出通道的新K
print(K.shape)   # torch.Size([3, 2, 2, 2])  : 輸出通道為3，輸入通道為2，h、w分別為2
print("新的K:",K)
print(corr2d_multi_in_out(X,K))

1x1卷積

驗證一下 1x1的卷積 等價于 一個全連接

# 【定義一個用全連接實現 1x1的 多輸入多輸出通道 的互相關操作】1×1卷積的多輸入、多輸出通道運算
def corr2d_multi_in_out_1x1(X,K):c_i, h, w = X.shape # 輸入的通道數、寬、高c_o = K.shape[0]    # 輸出的通道數X = X.reshape((c_i, h * w)) # 拉平操作（把高寬拉成一個向量），每一行表示一個通道的特征。此時X是一個矩陣K = K.reshape((c_o,c_i))  #  原K完整是  co x ci x 1 x 1，去掉1x1后 ，K也是一個矩陣Y = torch.matmul(K,X) return Y.reshape((c_o, h, w))X = torch.normal(0,1,(3,3,3))   # norm函數生成0到1之間的(3,3,3)矩陣 
K = torch.normal(0,1,(2,3,1,1)) # 輸出通道是2，輸入通道是3，核是1X1Y1 = corr2d_multi_in_out_1x1(X,K)
Y2 = corr2d_multi_in_out(X,K)
assert float(torch.abs(Y1-Y2).sum()) < 1e-6
print(float(torch.abs(Y1-Y2).sum()))

QA

20.輸入通道基本是固定的， 因為輸入是給定的。輸出通道理論上可以設為任意值（雖然實際上肯定不能隨便設）

【直觀理解】一般來說，輸入和輸出的數據 高寬不變時， 輸出通道也會設為和輸入通道一致。
但是如果輸出的數據 高寬都減半了，那么 輸出通道數 會 設為 輸入通道數的二倍（即 把空間信息壓縮了， 并把提取出的信息在更多的通道上存儲起來）

21.不會影響模型的精度、模型的性能（當然 很多0會影響計算性能，計算變慢了）

22.每個通道上的卷積核是不一樣的；（一般來說）不同通道的卷積核大小是一樣的，這樣方便計算、計算上的效率更高（當然理論上也可以讓不同通道的卷積核大小不同）

23.偏移的影響并不是很大（況且后續還有BN的存在），而且幾乎不會對計算性能產生影響

24.核的參數是學習出來的

不是的。有深度圖信息后要使用三維卷積，此時輸入數據變為 4D的（即 輸入通道 x 深度 x 寬 x 高），核變為5D的，輸出為4D的

26.對于多輸入通道，一個輸入通道有一個卷積核 得到一個計算結果， 多個輸入通道計算結果會累加。
多輸出通道數 取決于c_o，與 多輸入通道數的獨立的，

三維卷積核是五維的， 含 輸入通道、輸出通道、高、寬、深度信息

27.信號處理區分高低頻，圖像里面好像不太注重這個。 數據丟進去 網絡自己學習

28.卷積核的高寬均為1，每次只看一個像素（即不看 周圍空間的特征，即其不識別空間信息，不看當前這個像素與周圍其他像素的關系）

29.是的。這個就是mobile net（音譯，移動端用的卷積神經網絡，計算復雜度很低）

30.卷積有位置信息，而且對位置很敏感。
輸出數據中第i行第j列的元素 就是對應 輸入數據中第i行第j列元素附近那一塊的信息。
因此 卷積輸出的那些信息、位置信息 是 輸出的元素在矩陣中的位置決定的，后續會講基于 池化層 使得不對位置那么敏感。

31.通道之間是不共享參數的，我們希望每個通道能學習到不同的東西、模式。
彈幕說：同一卷積層共享參數，通道之間的不共享
卷積層參數共享指的是整個圖像用同一個卷積核來掃描，和全連接網絡相比共享了參數。

可以把 計算復雜度中的 mh和mw用 含nh nw去替換，因為 mh mw就是通過nh nw計算出來的。
只是用mh、mw表示 會簡單一點，且可以直觀看出 計算復雜度與 輸出數據中高寬的關系

33.同32

34.我們無法控制每個卷積核究竟能提取到什么信息，核參數都是學習出來的。
當然 一般需要多次卷積 即深度卷積神經網絡。

35.需要save和load
老師一般用 vim + VSCode
彈幕說：Vscode安裝jupyterlab插件，簡直不要太爽

36.正確。

37.feature map就是卷積的輸出

38.輸入通道不是動態變化的。

39.奇數在padding時方便一點。

40.rgbd可以用3D卷積，也可以用2D卷積（每個深度做一個2D卷積，然后用RNN或直接concat起來）

本次課程不會講3D卷積，其在視頻中用的多，其效果稍微比2D卷積好一點點、但是計算復雜度高很多