歡迎來到博主的專欄——C語言數據結構
博主id：代碼小豪

棧

棧是一個特殊線性表，其只能在表尾進行數據的插入與刪除，進行數據的插入與刪除的一端稱為棧頂 （TOP）。

我們可以將棧想象成一個酸菜壇子，往壇子中開始放菜的時候，壇中的酸菜是從底部開始增加的。

當壇子放滿酸菜后，我們開壇取出酸菜，酸菜會從頂部開始減少。

棧的順序存儲結構

前面提到了，棧是一個特殊的線性表，所以棧的儲存形式也可以像線性表一樣分為兩種，一種為順序存儲結構的棧（順序棧）。

既然順序棧是用順序結構實現的，那么就可以用數組來實現順序棧。

順序棧的結構聲明如下：

typedef int SDataType;
typedef struct SeqStack
{SDataType val[MAXSIZE];int TOP;
}SeqStack;

棧的插入

從棧頂插入數據的操作被稱為入棧（PUSH）

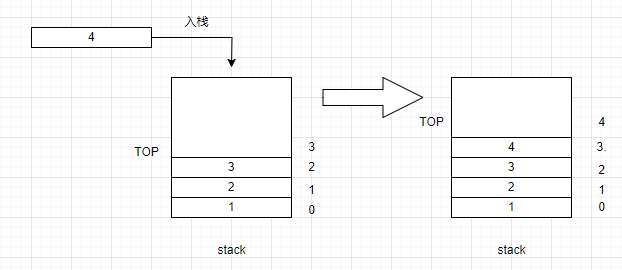
將數據插入棧頂的位置，然后棧頂的位置往上挪動一位，用于下一次入棧操作。

當棧為空時，棧頂的位置為0.

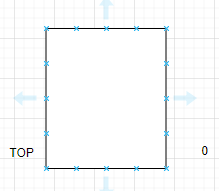
還有一種空棧的表示方法，由于數組中第一個元素的下標是0，但是空棧就代表著0下標處沒有元素，所以空棧時，棧頂的位置為-1.

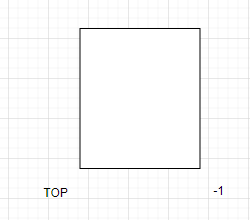
如果用這個方法表示的空棧，在插入數據時應該先讓棧頂往上一步，再插入數據。

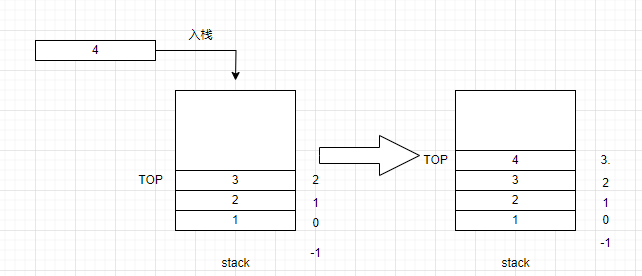
void StackPush(SeqStack* stack, SDataType e)
{if (stack->TOP == MAXSIZE){perror("stack overflow\n");return;}stack->val[stack->TOP] = e;stack->TOP++;
}

空棧的初始化

將一個新生成的棧傳入函數進行初始化，初始化的方法根據入棧的形式而定（TOP為0或TOP為-1）

以前者為例，空棧的初始化的函數為

void StackInit(SeqStack* stack)
{stack->TOP = 0;
}

棧的刪除

從棧頂刪除數據的操作稱為出棧（POP）

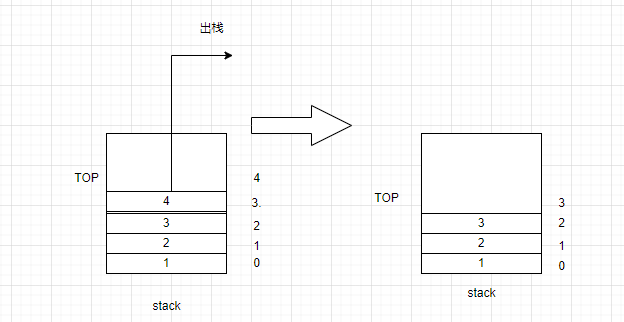
出棧的方式很簡單，我們不用將當前棧頂的數據進行處理，只需要將TOP的位置往下移動一格就行。

要注意當棧為空棧時的特殊情況，當棧為空棧時，出棧的操作會導致TOP位于非法的位置，當下次進行入棧操作時，就會發生數組越位的錯誤發生。

判斷空棧

判斷空棧的條件需要按照初始化時，棧頂的位置為準，以前者為例

bool StackEmpty(SeqStack* stack)
{return stack->TOP == 0;
}

如果TOP為0，那么該函數返回值為true。反之為false。

出棧的函數需要調用判斷空棧的函數，如下：

void StackPop(SeqStack* stack)
{if (StackEmpty(stack)){perror("stack is empty\n");return;}stack->top--;
}

讀取棧頂元素數據

SDataType StackTop(SeqStack* stack)
{return stack->val[stack->top - 1];
}

實現順序棧的所有代碼

typedef int SDataType;
typedef struct SeqStack
{SDataType val[MAXSIZE];int top;
}SeqStack;void ListStackInit(ListStack* stack)
{assert(stack);stack->top = NULL;stack->lenth = 0;
}void ListStackPush(ListStack* stack, LDataType e)
{StackNode* newnode = malloc(sizeof(StackNode));assert(newnode);newnode->val = e;newnode->next = stack->top;stack->top = newnode;stack->lenth++;
}bool ListStackEmpty(ListStack* stack)
{return stack->top == NULL;
}void ListStackPop(ListStack* stack)
{if (!ListStackEmpty(stack)){perror("stack is empty\n");return;}StackNode* del = stack->top;stack->top = stack->top->next;free(del);
}LDataType ListStackTop(ListStack* stack)
{assert(stack);return stack->top->val;
}

棧的鏈式存儲結構

棧既然是線性表，就可以用鏈表的形式來實現。

棧是從表尾進行插入和刪除，鏈表可以用尾插\尾刪的方法實現出棧和入棧（？）。

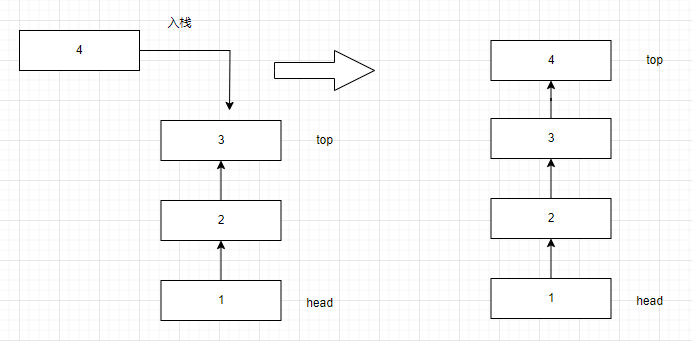
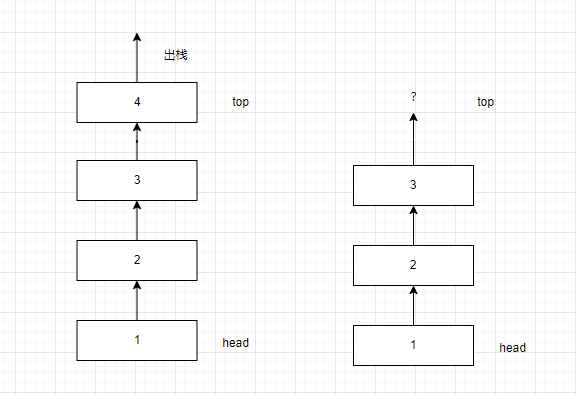
可以發現，使用尾刪法是不能實現出棧操作的，因為單鏈表不能將TOP回到上一個數據的位置。

為了解決這個問題，我們將TOP的位置變為鏈表頭，將入棧和出棧的操作用頭插\頭刪法來實現。

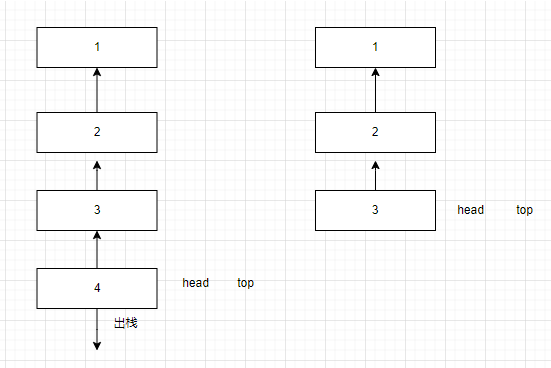
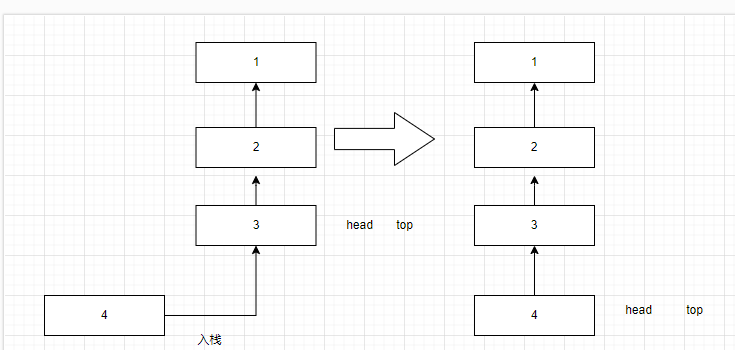
鏈式棧的結構類型如下：

typedef int LDataType;
typedef struct StackNode
{LDataType val;struct StackNode* next;
}StackNode;typedef struct ListStack
{StackNode* top;int lenth;
};

鏈式棧的初始化

鏈式棧的初始化如下

void ListStackInit(ListStack* stack)
{assert(stack);stack->top = NULL;stack->lenth = 0;
}

鏈式棧的入棧操作

鏈式棧入棧使用頭插法。代碼如下：

void ListStackPush(ListStack* stack, LDataType e)
{StackNode* newnode = malloc(sizeof(StackNode));assert(newnode);newnode->val = e;newnode->next = stack->top;stack->top = newnode;stack->lenth++;
}

鏈式棧的出棧操作

考慮到鏈表空棧無法出棧，所以先定義一個判斷空棧的函數

bool ListStackEmpty(ListStack* stack)
{return stack->top == NULL;
}

鏈式棧出棧使用頭刪法。代碼如下：

void ListStackPop(ListStack* stack)
{if (ListStackEmpty(stack)){perror("stack is empty\n");return;}StackNode* del = stack->top;stack->top = stack->top->next;free(del);
}

實現鏈式棧的所有代碼

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int LDataType;
typedef struct StackNode
{LDataType val;struct StackNode* next;
}StackNode;typedef struct ListStack
{StackNode* top;int lenth;
}ListStack;void ListStackInit(ListStack* stack);
void ListStackPush(ListStack* stack,LDataType e);
void ListStackPop(ListStack* stack);
bool ListStackEmpty(ListStack* stack);
LDataType ListStackTop(ListStack* stack);void ListStackInit(ListStack* stack)
{assert(stack);stack->top = NULL;stack->lenth = 0;
}void ListStackPush(ListStack* stack, LDataType e)
{StackNode* newnode = malloc(sizeof(StackNode));assert(newnode);newnode->val = e;newnode->next = stack->top;stack->top = newnode;stack->lenth++;
}bool ListStackEmpty(ListStack* stack)
{return stack->top == NULL;
}void ListStackPop(ListStack* stack)
{if (ListStackEmpty(stack)){perror("stack is empty\n");return;}StackNode* del = stack->top;stack->top = stack->top->next;free(del);
}LDataType ListStackTop(ListStack* stack)
{assert(stack);return stack->top->val;
}