Grid-Based Continuous Normal Representation for Anomaly Detection 論文閱讀
- 摘要
- 簡介
- 方法
- 3.1 Normal Representation
- 3.2 Feature Refinement
- 3.3 Training and Inference
- 4 實驗結果
- 5 總結
文章信息:

原文鏈接:https://arxiv.org/abs/2402.18293
源碼地址:https://github.com/laozhanger/GRAD
摘要
最近在無監督方式下,異常檢測領域取得了重大進展,其中僅有正常圖像用于訓練。幾種最新的方法旨在基于記憶檢測異常,通過比較輸入和直接存儲的正常特征(或使用正常圖像訓練的特征)。然而,這種基于記憶的方法在離散特征空間上操作,通過最近鄰或注意機制實現,存在泛化能力差或者輸出與輸入相同的身份捷徑問題。此外,現有方法中大部分設計用于檢測單一類別的異常,當面對多類別對象時性能不理想。為了解決上述所有挑戰,
我們提出了GRAD,一種新穎的異常檢測方法,用于在“連續”特征空間中表示正常特征,通過將空間特征轉換為坐標并將其映射到連續網格來實現。
此外,我們精心設計了專為異常檢測定制的網格,有效表示局部和全局正常特征,并有效地融合它們。
我們的大量實驗證明,GRAD成功地泛化了正常特征并減輕了身份捷徑問題,此外,由于高粒度全局表示,GRAD有效地處理了單一模型中的多樣類別。
在使用MVTec AD數據集進行評估時,GRAD在多類別統一異常檢測方面減少了65.0%的錯誤,顯著優于先前的最先進方法。項目頁面位于 https://tae-mo.github.io/grad/。
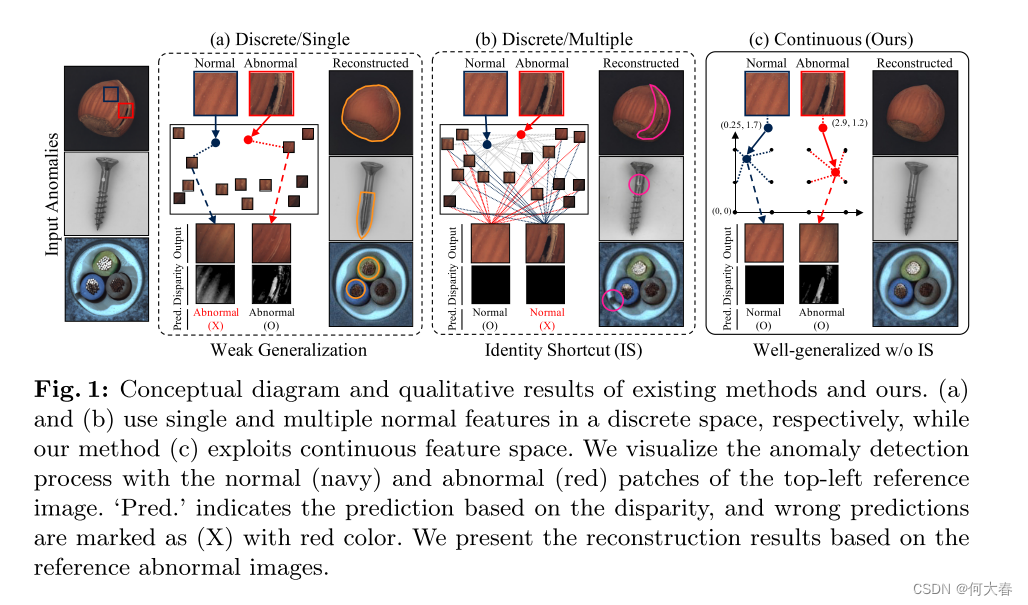
簡介
在這項工作中,作者提出了將網格表示結合到異常檢測中以實現高性能。
主要貢獻:通過將離散特征存儲替換為連續網格來表示正常特征,從而解決了上述討論的挑戰性問題,并實現了高性能。
方法
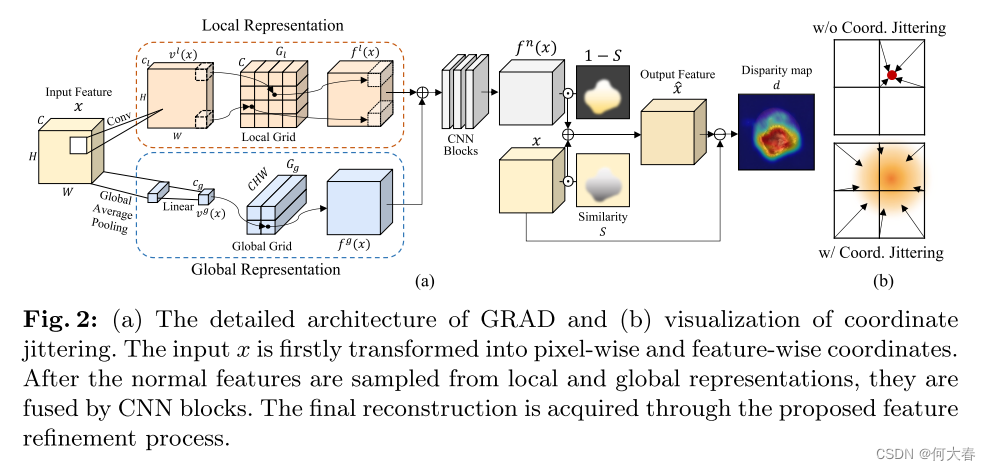
Background.為了幫助讀者理解GRAD,我們首先描述了網格操作。網格被訓練為坐標的函數,具有無限分辨率,輸出與坐標對應的特征。無限分辨率下的輸出特征是通過網格中附近特征的聚合得到的,基于輸入坐標和相鄰特征之間的距離。例如,當我們進行一維網格采樣 ? ( ? ; G ) : R → R C ?(·; G) : \mathbb{R} → \mathbb{R}^C ?(?;G):R→RC 時,具有C個通道的輸出特征是通過一維網格 G ∈ R R × C G ∈ \mathbb{R}^{R×C} G∈RR×C 的相鄰值進行插值得到的,數學上可以表示如下:
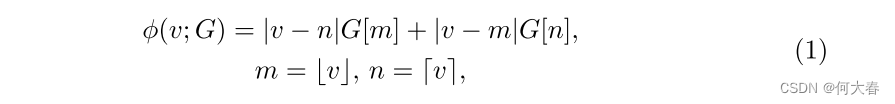
其中, v ∈ R v ∈ \mathbb{R} v∈R 是一個任意的輸入坐標,被歸一化為網格分辨率 R R R,而 G [ i G[i G[i] 表示來自網格 G G G 的索引 i i i 處的特征。 m m m 和 n n n 是要參考的索引, ? ? ? ?·? ??? 和 ? ? ? ?·? ??? 分別表示向下取整和向上取整操作。上述方程可以通過對D維網格的 2 D 值 2^D值 2D值進行插值,簡單地擴展到更高維度 D D D(例如,在圖1( c )中的2D網格中的4個值)。
Overview.我們的工作動機是利用網格操作在連續空間中有效表示正常特征,與離散空間有所區別。以無監督的方式,GRAD基于輸入特征和輸出正常特征之間的差異來檢測異常圖像和區域,如圖2(a)中所描述的。因此,GRAD的主要目標是有效地保留正常成分(例如,形狀或紋理),同時消除特征內存在的任何異常。
為此,我們在訓練階段將正常特征表示為連續空間中的正常表示,這在測試階段用于替換異常特征。我們描述了GRAD如何在連續空間中表示正常特征并獲取輸出特征 x ^ \hat{x} x^,基于從預訓練骨干網絡提取的輸入特征 x x x,其中 x x x, x ^ ∈ R C × H × W \hat{x} ∈ \mathbb{R}^{C×H×W} x^∈RC×H×W, C 、 H 、 W C、H、W C、H、W 分別是特征的通道數、高度和寬度。
3.1 Normal Representation
GRAD的基本概念是將輸入特征轉換為連續值的特定坐標,然后將這些坐標映射到特征網格上。特別地,我們設計了從局部和全局視角表示正常特征。通過結合每個視角的獨特特征,得到的特征可以提供對輸入的強大表示,捕捉細粒度的細節以及更廣泛的整體結構。
Local representation.
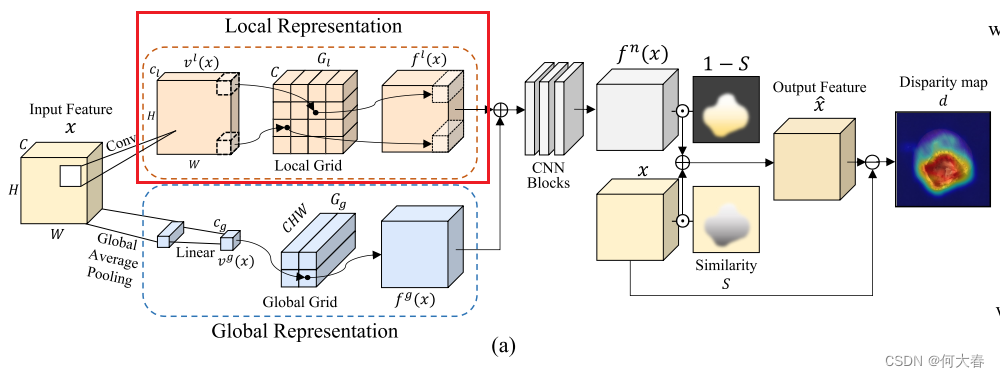
如圖2(a)所示,GRAD對特征的每個像素進行采樣,以表征圖像的每個補丁,以表示局部特征。然后,通過具有1個卷積核大小的卷積層將每個像素的通道轉換為相應的坐標(低維向量),然后進行雙曲正切激活。利用這些逐像素的坐標,我們從局部網格表示中獲取采樣的正常特征。更正式地,我們定義一個函數 v l ( ? ) : R C × H × W → R C l × H × W v^l(·) :\mathbb{R}^{C×H×W} → \mathbb{R}^{C_l×H×W} vl(?):RC×H×W→RCl?×H×W,根據輸入特征生成逐像素的坐標,其中 C l C_l Cl?是生成坐標的維度。給定逐像素的坐標 v h , w l ( ? ) ∈ R C l v^l_{h,w}(·) ∈ \mathbb{R}^{C_l} vh,wl?(?)∈RCl?,從具有每個維度分辨率 R l R_l Rl?和通道數 C C C的 C l C_l Cl?維網格 G l G_l Gl?中采樣正常特征。局部表示 f l ( x ) : R C × H × W → R C × H × W f^l(x) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C×H×W} fl(x):RC×H×W→RC×H×W 的方程如下所示:
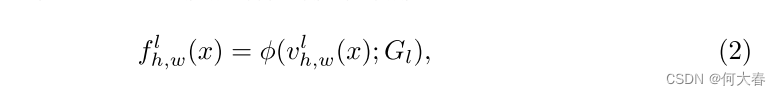
其中, ? ( ? ; G l ): R C l → R C ?(·; G_l):\mathbb{R}^{C_l}→\mathbb{R}^C ?(?;Gl?):RCl?→RC表示通過基于坐標對網格值進行雙線性內插來從網格 G l G_l Gl?采樣特征。
由于特征的每個像素都表征圖像中的一個補丁,局部表示確保保留正常補丁,并用具有相似局部上下文的正常補丁替換異常補丁。因此,當輸入一個正常補丁時,即使在訓練補丁中沒有完全匹配的情況下,也可以通過插值映射到附近坐標的正常特征來表示相應的正常特征。
此外,對于異常補丁,GRAD基于減少的坐標找到一個最能代表異常補丁的正常特征。由于在訓練過程中網格從未暴露于異常特征,它無法通過插值附近的正常特征來表示異常特征。這是我們如何有效解決現有方法中經常出現的基于注意機制聚合大量特征的相似性而產生的身份捷徑(IS)問題的核心思想。
Global representation.異常區域不僅可能存在于圖像的局部,還可能存在于全局范圍內。為了處理這樣的全局異常情況,GRAD維護另一個網格表示來捕獲圖像的全局特征。與局部表示類似,我們制定了一個函數來獲取全局特征坐標 v g ( ? ) : R C × H × W → R C g v^g(·) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C_g} vg(?):RC×H×W→RCg? ,其中 C g C_g Cg?是坐標的降維維度。對于函數 v g ( ? ) v^g(·) vg(?),我們采用了全局平均池化和線性層,如圖2(a)所示。特征級的坐標通過具有每個維度分辨率 R g R_g Rg?的 C g C_g Cg?維網格 G g G_g Gg?映射到每個正常特征。網格 G g G_g Gg?的一個元素是一個 C H W CHW CHW維向量,一旦被采樣,它就被重塑為 C × H × W C×H×W C×H×W張量。全局表示 f g ( x ) : R C × H × W → R C × H × W f^g(x) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C×H×W} fg(x):RC×H×W→RC×H×W的方程表示如下:
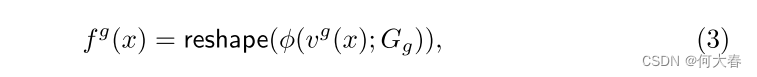
其中, ? ( ? ; G g ): R C g → R C H W ?(·; G_g):\mathbb{R}^{C_g}→\mathbb{R}^{CHW} ?(?;Gg?):RCg?→RCHW表示通過雙線性插值從網格 G g G_g Gg?采樣特征,并且 r e s h a p e ( ? ): R C H W → R C × H × W reshape(·):\mathbb{R}^{CHW} → \mathbb{R}^{C×H×W} reshape(?):RCHW→RC×H×W表示整形操作。
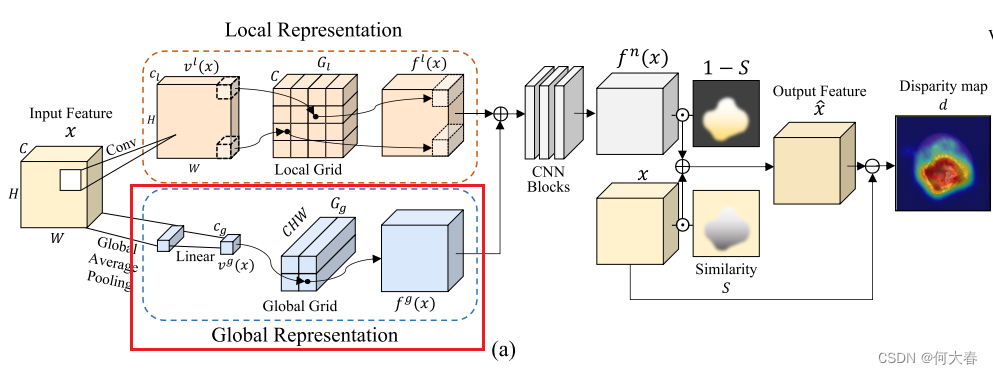
Fused representation.我們將局部和全局表示 f l ( x ) f_l(x) fl?(x)和 f g ( x ) f_g(x) fg?(x)組合起來,以有效地學習正常表示 f n ( x ) f_n(x) fn?(x),如圖2(a)所示。局部和全局表示被連接起來,然后被送入以下卷積網絡 ψ ( ? ) : R 2 C × H × W → R C × H × W ψ(·) : \mathbb{R}^{2C×H×W} → \mathbb{R}^{C×H×W} ψ(?):R2C×H×W→RC×H×W來重構 f n ( x ) f_n(x) fn?(x),如下所示:
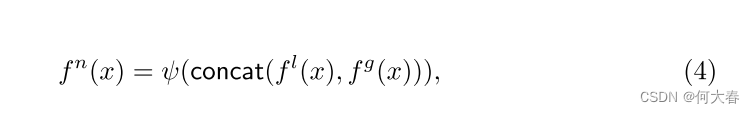
其中, c o n c a t ( ? , ? ) concat(·, ·) concat(?,?)表示沿著通道軸拼接兩個特征。通過融合局部和全局表示,GRAD可以從細粒度的細節到更廣泛的上下文中表示正常特征,相比僅使用其中之一,可以獲得更高的性能(見第4.4節中的消融研究)。
3.2 Feature Refinement
盡管局部和全局正常表示已經融合,但在 f n ( x ) f_n(x) fn?(x)和 x x x之間仍然可能存在正常區域的偏差,這可能導致錯誤檢測(即假陽性)。因此,在特征細化中,我們的目標是在應該是正常但與 x x x有偏差的區域中對 f n ( x ) f_n(x) fn?(x)進行細化,以減少假陽性。為了識別這樣的區域,我們通過結合均方誤差(MSE)和余弦相似度評估 x x x和 f n ( x ) f_n(x) fn?(x)之間的逐像素相似性。這兩個指標提供了正常和異常特征之間差異的全面視角,其中 M S E MSE MSE捕捉絕對強度差異,而余弦相似度則表征結構和位置的相似性。通過考慮組合相似性 S ∈ R H × W S ∈ R^{H×W} S∈RH×W,我們可以重構 x ^ \hat{x} x^如下:
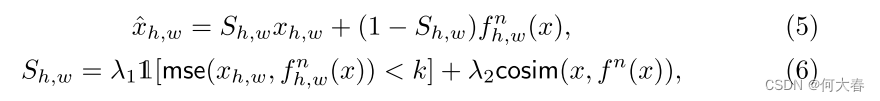
其中, h h h和 w w w是空間特征的索引, 1 [ ? ] \mathbb{1}[·] 1[?]是指示函數, m s e ( ? , ? ) mse(·, ·) mse(?,?)和 c o s i m ( ? , ? ) cosim(·, ·) cosim(?,?)分別是均方誤差和余弦相似度。為了將MSE作為相似性的度量,我們根據其是否超過閾值k將MSE值轉換為0或1。
3.3 Training and Inference
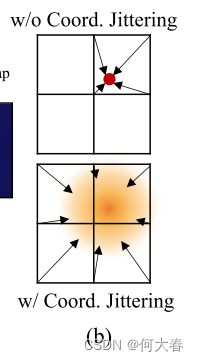
Coordinate jittering.為了實現更廣義的網格表示,我們在訓練階段對局部坐標 v l ( x ) v_l(x) vl?(x) 應用高斯噪聲。例如,沒有抖動時,在二維網格中,一個坐標影響最多四個網格值,如圖2(b)所示。相比之下,當擾動坐標時,我們可以在每次迭代中使用鐘形分布更新更多的網格值,從而產生更廣義的網格。
Training.
給定 x x x和GRAD導出 x ^ \hat{x} x^,我們采用MSE損失作為目標函數,如下所示:

根據公式(7),我們以端到端的方式學習整個模型,包括由Xavier正態初始化[12]初始化的網格。由于在訓練階段 x x x始終是正常輸入,因此網格被學習用于表示正常特征。
Inference.
為了通過 x x x和 x ^ \hat{x} x^之間的差異進行異常檢測和定位,我們制定了異常分數圖 d ∈ R H × W d ∈ \mathbb{R}^{H×W} d∈RH×W如下所示:
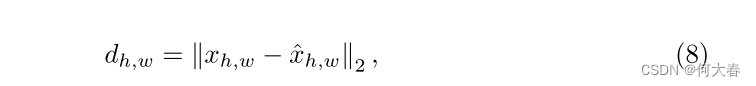
其中, h h h和 w w w表示每個像素的位置。為了與相應的真實情況相匹配, d d d被插值到輸入的原始形狀中。通過從平均池化的 d d d中取最大值,可以獲得每個圖像的異常分數,并且插值后的異常圖本身用于像素級異常分數。
4 實驗結果
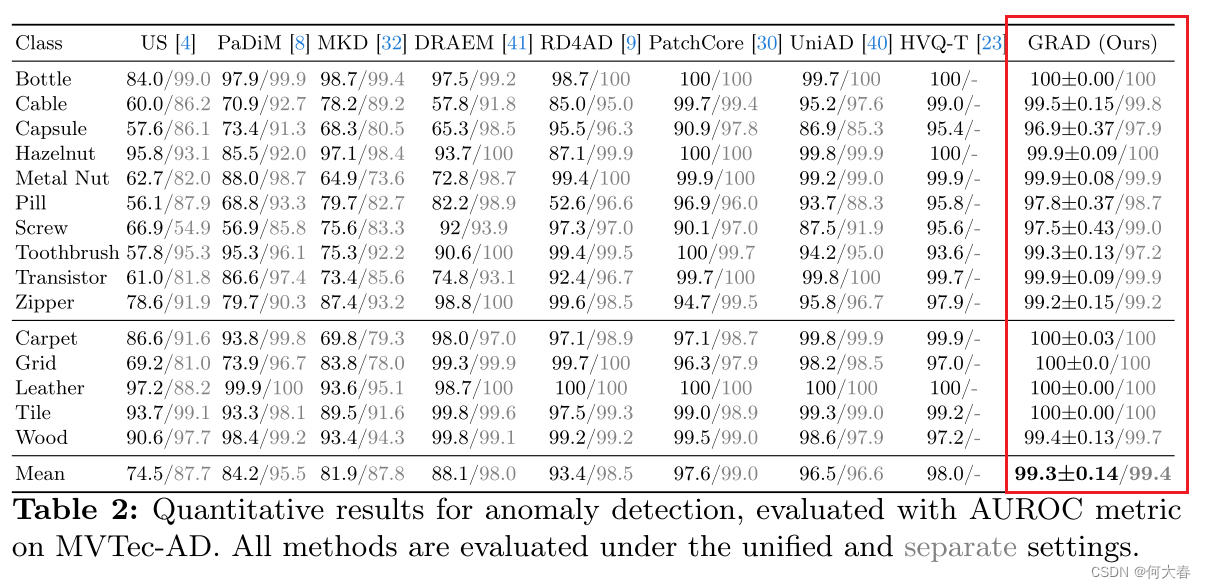
異常檢測
異常定位
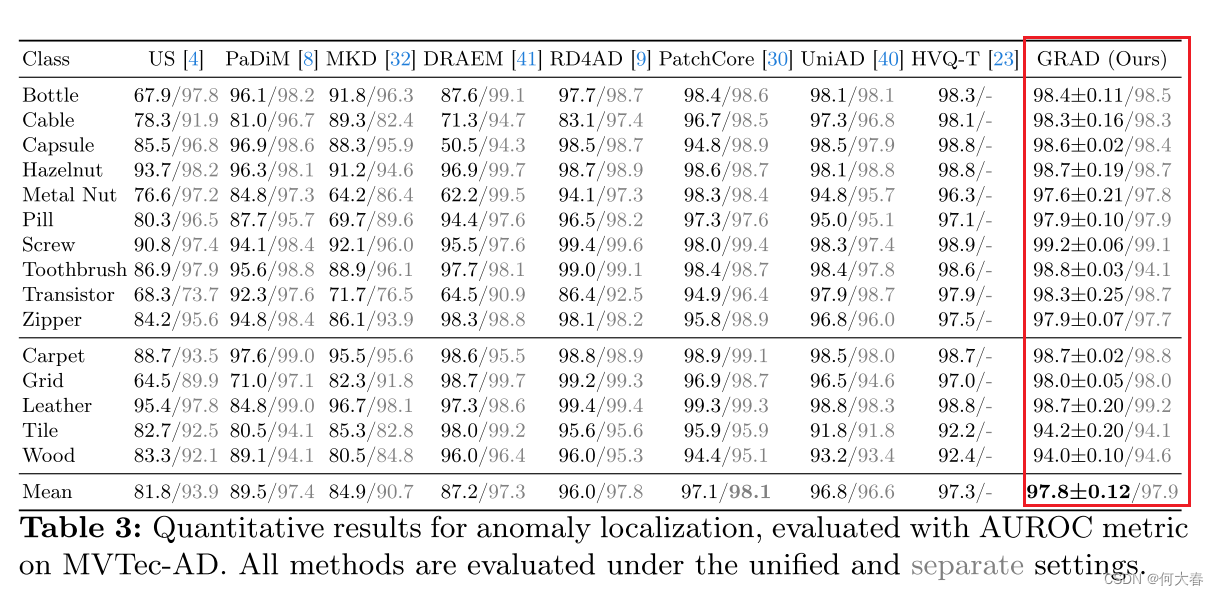
5 總結
在這項工作中,作者提出了一種新穎的異常檢測架構,名為GRAD,它在連續空間中表示正常特征,與之前局限于離散空間的方法不同。GRAD成功地在連續空間中表示了局部和全局特征,同時克服了現有方法的諸多局限,如泛化能力弱、身份捷徑、計算復雜度和參數效率等。通過大量實驗,作者定性和定量地展示了GRAD的有效性。通過特征細化和坐標抖動,GRAD取得了顯著優勢的最先進性能。

,Lab: Copy-on-Write Fork)
)
















