光柵化算法

多數計算機圖形圖像，是通過光柵顯像顯示給用戶的，這種系統將圖像作為像素陣列進行顯示，像素（pixel）即圖像元素（picture element）的簡稱。這些像素采用RGB顏色空間。本文討論光柵顯像的基本原理，著重討論RGB顏色系統和標準圖像顯示器存在的非線性。

1.光柵顯像

臺式機和投影顯示器的顯示技術有多種。這些顯示器的分辨率（像素數量）和物理尺寸各不相同，編程人員通常假設像素排成矩形陣列，又稱為光柵（raster）。

像素

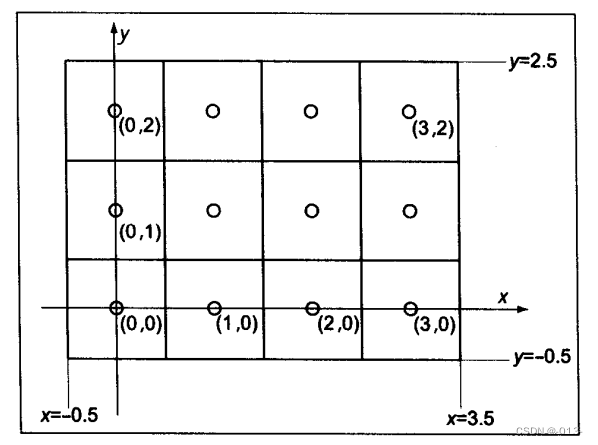
光柵顯示器上的可顯示元素稱為像素。在顯示器上，通常用有序對(i,來表示像素的索引,即表示該像素所在的行與列。如果一臺顯示器具有n,行、n,列像素，則左下角的元素是像素(0,0)右上角的元素是像素(nx-1,ny-1)

我們需要用實際的二維屏幕坐標來表示像素的位置。隨著API的不同，這些系統在細節上會有所不同，但是最常使用的是用整數點陣作為像素的中心，如圖,4x3屏幕所示。由于像素占據一定的空間區域，所以距離像素中心具有0.5個單位的過沖(overshoot)。

2.顯示器亮度和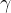 $\gamma$ 值

現在所有的顯示器都采用數字信號輸入方式，接收的是用數字信號表示的像素“值”，然后將其轉化為亮度值。斷電后顯示器的亮度實際上不是零，因為屏幕能夠反射環境光線。但我們可以認為此時顯示器呈“黑色”，顯示器完全打開時呈“白色”。對像素顏色用0到1的數值來表示。黑色為0，白色為1，介于黑白中間的中間灰色為0.5。注意這里“中間”指的是從像素發出光線的強度，而不是指觀察到的亮度。人類對光強的感知呈非線性，這不是我們現在討論的內容。

為了在顯示器上產生圖像，要先明白兩個關鍵問題。第一，顯示器對輸入信號的處理是非線性的。例如，如果輸入三個像素值0、0.5、1.0，顯示的亮度則可能是0、0.25、1.0(也就是0、打開1/4、完全打開)。對于多數顯示器，一般利用 $\gamma$ 值來近似表示其非線性，具體數值就是下面公式中的指數:

顯示亮度=(最大亮度) $a^{\gamma }$

其中a是介于0到1之間的輸入亮度值。例如，如果顯示器的y值為2.0，輸入值為a=0.5，則顯示亮度是最大亮度的1/4，因為0.52=0.25。不管值為多少，a=0對應顯示亮度為0，a=1對應最大顯示亮度。用y值表示顯示器的非線性只是一階近似,實際中在估計設備的y值時不需要很高的精度。一種度量非線性的直觀方法是，找到能產生黑白之間的中間亮度的a值，即下式中的a值:

0.5= $a^{\gamma }$

如果能找到滿足上式的a值，則通過兩邊取對數就可以求出y值:

$\gamma =\frac{ln0.5}{lna}$

標準求a值的方法是，顯示黑白相間的像素棋盤模式，如圖是具有a值的灰色像素方陣.當從遠處觀察這幅圖像時(或者當你眼睛近視但沒帶眼鏡時)，如果a值正好是黑白的中間值，那么這幅圖像的左右兩邊看起來會大致一樣。這是因為，雖然存在很多的黑、白像素，但經棋盤模式混合，整體效果就顯示一致的中間色了。為了做好這個實驗，必須嘗試很多a值，直到53]找到需要的數值為止。可以為用戶提供一個滑動條來控制a值，或者將多個不同灰度的方塊同時與一個大的棋盤模式比較。值得注意的是，CRT沿水平方向快速改變亮度是有難度的，因此水平的黑白條紋要比棋盤模式效果好。利用人臉識別技術可使亮度匹配結果更加精確(Kindlmann，Reinhard,&Creem，2002)。

一旦知道了 $\gamma$ 值，就可以對輸入進行伽馬校正，使得輸入值a=0.5可以在屏幕上顯示出介于黑白中間的灰度效果。變換方法為：

$a = a^{\frac{1}{\gamma }}$

? ?把該式代入顯示亮度公式可得：

顯示亮度 = (最大亮度)?? $\left ( a^{^{\frac{1}{\gamma }}} \right ) \gamma$ ?= a 最大亮度

實際顯示器的另一個重要特征是，輸入值通常經過了量化處理。因此，我們可以在浮點范圍[0,1]內處理亮度值。輸入到顯示器的信息一般是大小固定的非負整數，取值范圍一般是0~255，可采用8位二進制數存儲。所以a的取值不是[0,1]中的數字，而是

a的取值 =? $\left \{ \frac{0}{255} ,\frac{1}{255},....,\frac{254}{255},\frac{255}{255}\right \}$

則顯示的亮度值近似為

$\left \{ M\left ( \frac{0}{255} \right )^{\gamma }, M\left ( \frac{1}{255} \right )^{\gamma }, M\left ( \frac{2}{255} \right )^{\gamma },..., M\left ( \frac{254}{255} \right )^{\gamma } M\left ( \frac{255}{255} \right )^{\gamma } \right \}$

M表示最大亮度。實際應用需要精確控制亮度值，我們要分出256個可能的亮度等級，而且這些亮度在屏幕的不同位置其值也有所不同，尤其是CRT顯示器更需要這樣做。視角不同也會影響亮度值。幸運的是，實際系統一般不需要做精確標定。

3.RGB顏色

計算機圖形學中，多數顯示效果都由紅綠藍（RGB）顏色空間確定。RGB顏色空間比較簡單，經轉換能夠直接控制多數計算機屏幕的顯示。

對于RGB加性顏色空間，我們有下列混合效果：

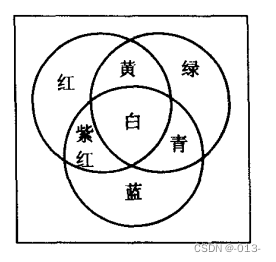
紅+綠=黃

綠+藍=青

藍+紅=紫紅

紅+綠+藍=白色

青色是一種藍綠色，紫紅色是一種紫色

所以只要讓基色光的強度由最小到最大變化，就能在RGB顯示器上顯示所有顏色。把單色的最亮狀態表示為1,則顏色值為0~1之間的分數。這樣就產生出一種三維RGB顏色立方體紅、綠、藍為坐標軸，坐標值從0到1變化。顏色立方體如圖：

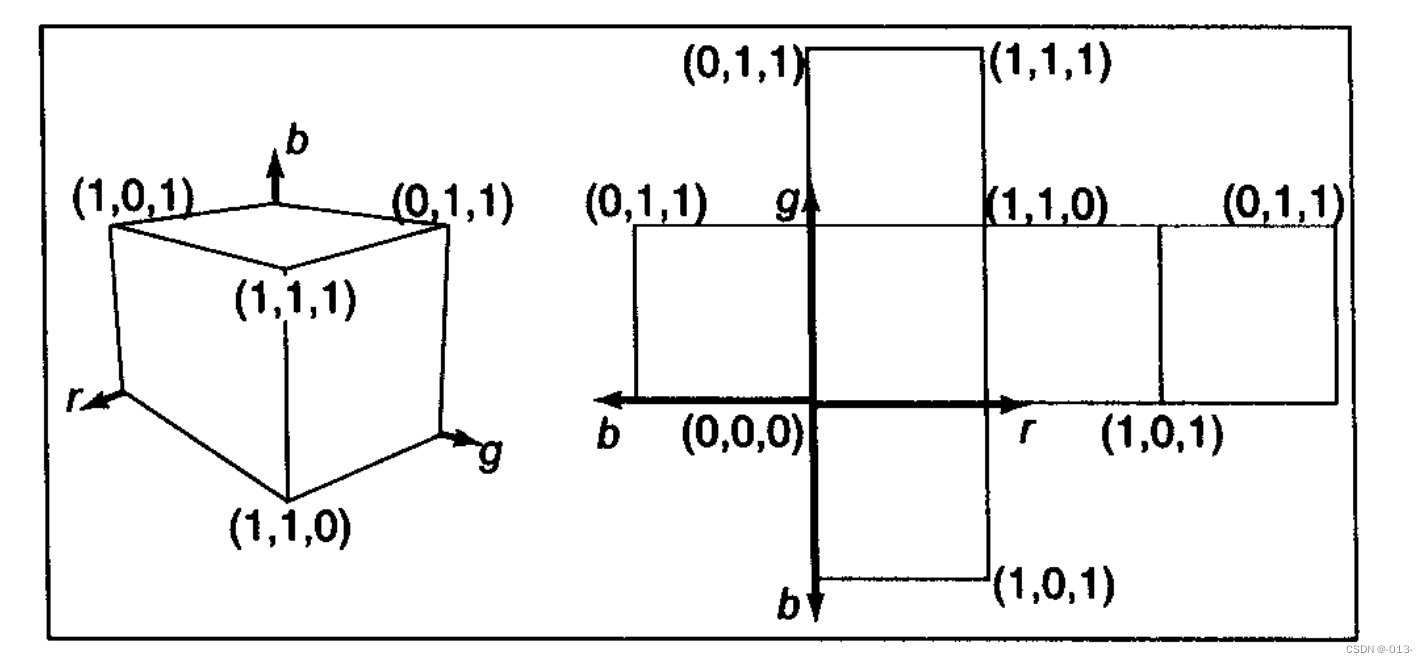
常見的RGB顏色坐標為：

黑色 = (0,0,0)
紅色 = (1,0,0)
綠色 = (0,1,0)
藍色 = (0,0,1)
黃色 = (1,1,0)
紫紅色 = (1,0,1)
青色 =(0,1,1)
白色 =(1,1,1)

實際RGB數值以量化形式給出，類似上面顯示器亮度和 $\gamma$ 值的灰度級，各成分都用數表示。常用的整數大小占一個字節，所以RGB的各成分是0~255之間的一個整數。三個整數共占用三個字節，也就是24位二進制數。因此，具有“24位顏色”的系統，三基色中的每一種都有256個等級。

4. $\alpha$ 通道

當我們想在背景上面插入一幅前景圖片，

對于不透明像素，我們只需要替換相應位置的背景像素即可。

對于完全透明的前景像素，背景像素不在改變。

對于半透明像素，為了將前景與背景混合，就要權衡像素作為前景的分數（fraction）。該分數用 $\alpha$ 表示。如果想把前景色 $c_{f}$ 與背景色 $c_{b}$ 混合，并且被前景覆蓋的像素的分數為 $\alpha$ ，那么就可以采用下面的計算公式計算

$c=\alpha c_{f}+(1-\alpha )c_{b}$

如下圖，圖中的 $\alpha$ 圖像可以存儲為RGB圖像，也可以存儲為單通道的灰度圖像。盡管使用率很高，但在很多情況下 $\alpha$ 以其他方式得到使用（Porter&Duff,1984）。

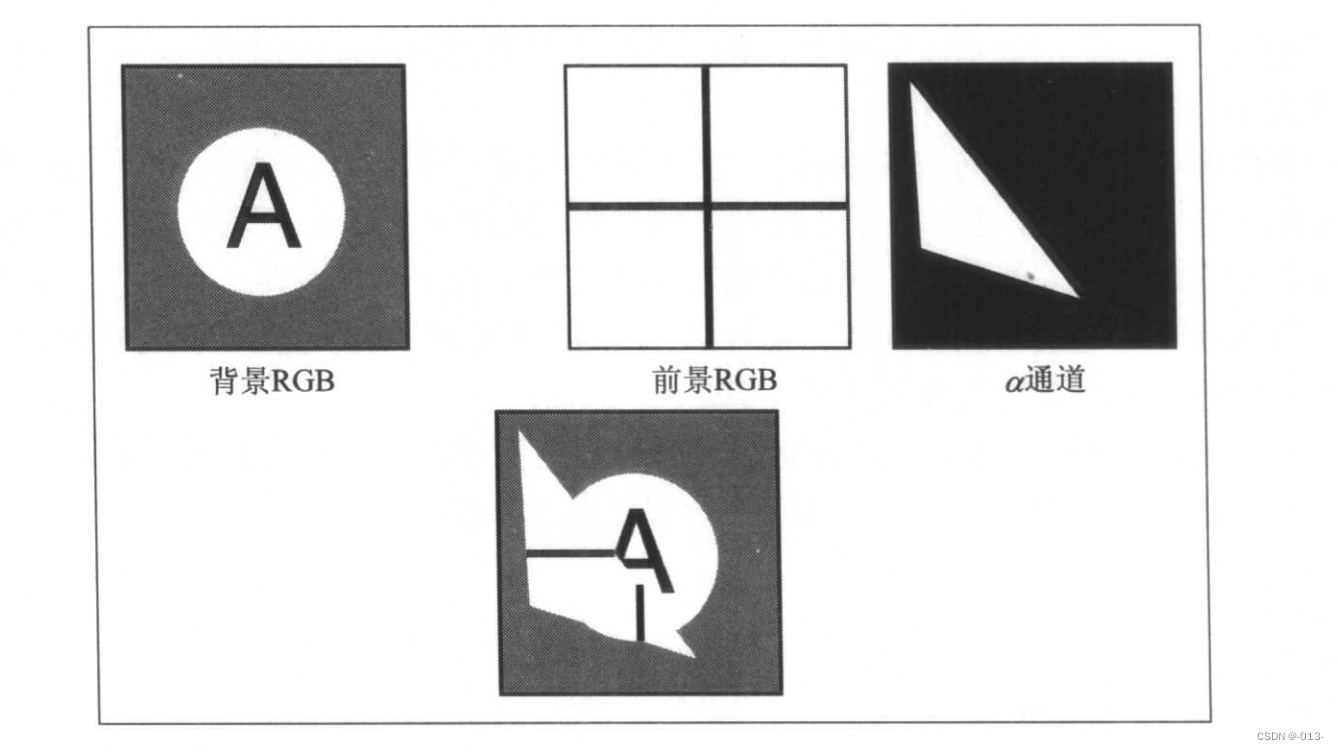
在前景圖像與背景圖像混合之前，先經過 $\alpha$ 通道進行了修剪處理。最下面是組合效果圖

5.直線繪制

多數圖形軟件都包含直線繪制命令，即捕捉屏幕上兩個點的坐標，并在它們之間畫一條直線。例如，如果發現兩個端點是(1,1)和(3,2)，那么就在屏幕上顯示這兩點，并在它們之間填上一個像素。對一般的屏幕坐標端點 $(x_{0},y_{0})$ 和 $(x_{1},y_{1})$ ，常規作法是在它們之間畫出合適的像素點集，這些點近似一條直線。為了簡化處理 $x_{0},x_{1},y_{0},y_{1}$ 的值經常規定為整數(像素中心)，因為直線本身就比較粗略，要求子像素精度不合適。在實現API時需要的是實數端點坐標，一般方法是將它們就近取整，這樣做比較合理，一般應用編程人員注意不到有什么不同。因為端點坐標是整數，在整數與浮點變量共同參與運算時，就要注意隱式類型轉換問題。我們基于直線方程進行直線繪制。有兩種類型的方程可供選擇:隱式方程和參數方程。下面講解基于這兩種方程的兩種算法。

基于隱式方程繪制直線

直線方程? y = ax+b 可以得出斜率?

? $a = \frac{y_{1} - y_{0}}{x_{1} - x_{0}}$

直線隱式方程

$f(x,y) = (y_{0} - y_{1})x + (x_{0} - x_{1}) + x_{0}y_{1} -x_{1}y_{0} = 0$

在下面的討論中都假設a∈(0,1]。類似地,可以推出a∈(-∞,-1]、a∈(-1,0]和a∈(1,∞)時的結果這4種情況覆蓋了所有的可能情況。
當m∈(0,1]時，直線在x軸上的變化速度大于在y軸上的變化速度。對于y軸方向向下的API,我們可能會想到情況是否變得復雜。實際上我們可以忽略這個細節。可以不考慮幾何上的“升”和“降”，因為兩種情況下的代數表示是一樣的。認真的讀者可以證明，得到的算法同樣適用于y軸向下的情況。中點算法的重要假設是，我們能繪出沒有間隔的最細的直線。兩對角像素之間的連接被認為不產生間隔。

繪制直線時，從左端點向右端點進行。只有兩種可能:繪制一像素時，和左邊所繪像素高度一樣，或者高出一個像素。在兩端點之間每一列,總是只有一個像素。沒有像素就意味著有間隔,有兩個像素則直線太粗。就我們正討論的情況來說，同一行上可以有兩個像素;因為直線更接近于水平，因此其走勢是向右或者向上。這種認識如圖所示，圖中顯示3條這樣的直線，每一條在水平方向的前進速度要比在垂直方向上快。?

針對m∈(0,1)情況的中點算法，首先建立最左邊的像素，以及最右邊像素的列號(x值)，然后沿水平循環建立每個像素的行號(y值)。該算法的基本形式如下:

$y=y_{0}$

for? x= $x_{0}$ ?to $x_{1}$ ? do?

????????draw(x,y)

????????if(some condition) then

y=y+1

其中的x和y都是整數。簡單地說就是“從左至右不斷繪制像素，在該過程中有時需要向y軸正向有所偏移”。關鍵是如何確定if語句中的條件。

一種有效方法是,參考兩候選像點之間的中點位置。更具體地說,對于剛繪制的像素點(x,y),它在屏幕上的坐標為(x,y)，下面要繪制的候選像素為(x+1,y)和(x+1,y+1)。兩候選像點之間的中點為(x+1,y+0.5)。如果直線通過中點的下方,就繪制下面的像素:如果直線通過中點的上方,就繪制上面的像素(見圖3)。

判斷直線是通過點(x+1,y+0.5)的上方還是下方。位于直線上的點(x,y)，滿足直線方程f(x,y)=0;位于直線一邊的點,滿足 f(x,y)>0;位于直線另一邊的點，滿足f(x,y)<0。由于-f(x,y)=0和 f(x,y)=0都可以作為直線的方程，所以很難利用f(x,y)的正負來快速判斷(x,y)究竟位于直線的上、下哪個方向。但是,可以通過分析算出來。y的項(x1-x0)y。要注意(x1-x0)肯定為正數因為x1>x0。這就意味著隨著y的增大,(x1-x0)y項的值將變大。因此f(x,+∞)肯定為正，并且位于直線的上方，也就是說直線上方的點都是正的。另一種判斷方法是，由于梯度向量中的y分量是正的，因此在直線的上方y可以任意增加，f(x,y)也就肯定是正的。于是，我們可以把if語句中的條件寫具體，代碼就更明確了:

$y=y_{0}$

for? x= $x_{0}$ ?to $x_{1}$ ? do?

????????draw(x,y)

????????if f(x+1,y+0.5) < 0 then

y=y+1

6.三角形光柵化

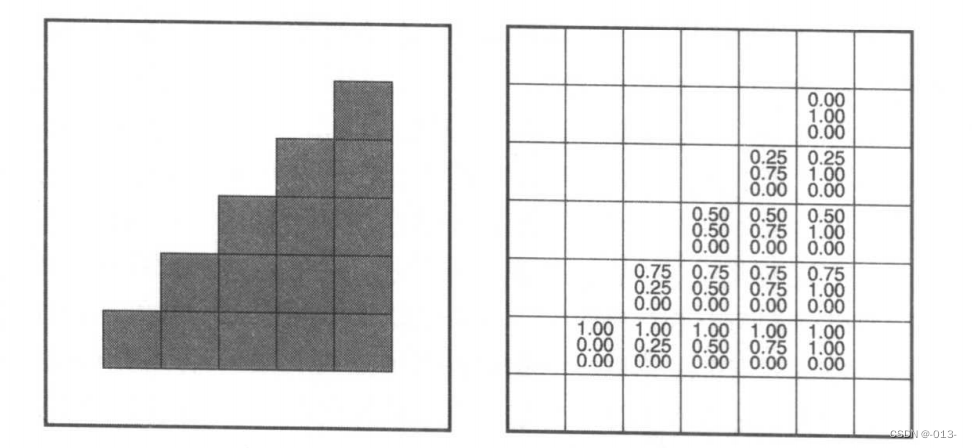
在屏幕坐標系中，我們經常想繪制一個過二維點p0=(x0,y0)、p1(x1,y1)、p2(x2,y2)的二維三角形。這與直線繪制問題類似，但是它也有自己的特別之處。已經證明端點采用整數坐標沒有什么益處，因此允許(x，y)具有浮點值。與直線繪制一樣，希望能根據頂點數值插入顏色或其他性質。如果存在重心坐標系，就可以直接計算插入值。例如，假設頂點的顏色為c0、c1、c2，在重心坐標為的三角形內部，某點的顏色值為

$c=ac_{0}+\beta c_{1}+yc_{2}$

這種顏色插值方法在圖形學中稱為Gouraud插值法，來源于提出該算法的作者(Gouraud，1971)的名字。
光柵化三角形的另一個特別之處是,我們通常對具有公共頂點和公共邊的那些三角形進行光柵化。這就意味著要光柵化的是相鄰三角形，因此沒有空隙。可以使用中點算法畫出每個三角形的輪廓，然后填入內部像素，從而實現三角形光柵化。因此，相鄰三角形在鄰邊處都繪制了相同的像素。如果兩相鄰三角形的顏色不同，則圖像將由兩個三角形被繪制的順序來確定。為了避免順序問題并且消除空隙，最常用的三角形光柵化方法是利用下列約定:當且僅當一個像素的中心位于三角形內部時，才繪制該像素。也就是說，像素中心的重心坐標都在區間(0,1)內。于是又產生了這樣的問題:如果像素的中心正好位于三角形的邊上，這時怎么辦?在后面將討論到，有好幾種方法來處理這種情況。關鍵結論是:當我們根據頂點插入顏色時，利用重心坐標可以確定是否該繪制一個像素，以及該像素應是什么顏色。于是問題變為如何能快速找到像素中心的重心坐標(Pineda，1988)。蠻力光柵化算法如下:

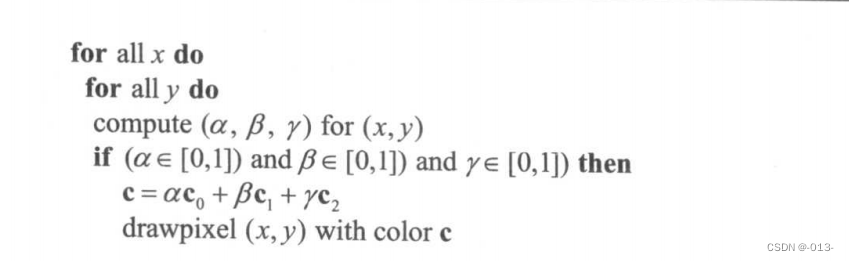
算法的其余部分把外部循環限制到更小的候選像素集，使重心計算快速有效。尋找三頂點的包圍矩形，只對該矩形內的候選像素執行循環，這樣就能提高算法的效率。計算重心坐標。于是算法變為:

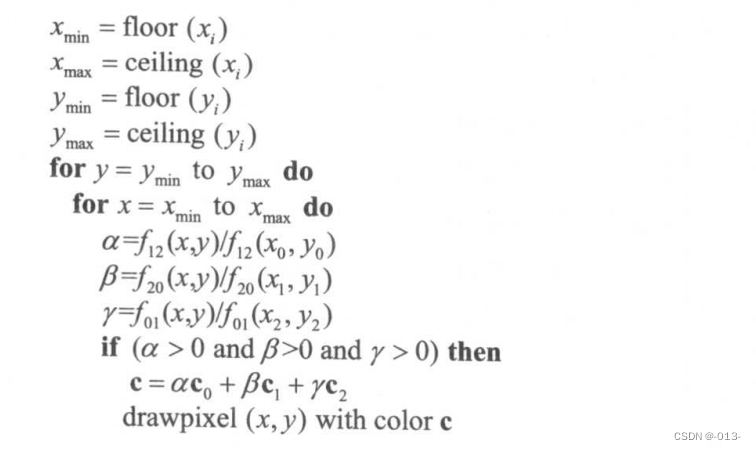
其中 $f_{ij}$ 是根據適當頂點，可以得出直線：

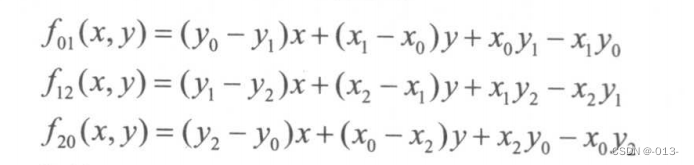
注意我們用判斷條件 a>0代替了 α∈(0,1)。原因是，考慮到 $\alpha$ + $\beta$ + $\gamma$ =1，那么如果 $\alpha$ 、 $\beta$ 、 $\gamma$ ?都是正的，它們必然都小于1。同樣，我們可以只算出三個重心坐標中的兩個，然后利用它們的這種關系計算另一個。和繪制直線的算法類似，這時的算法也可以是增量算法，但不清楚能否降低計算量。每次計算 $\alpha$ 、 $\beta$ 、 $\gamma$ ?，也就是計算f(x,y)=Ax+By+C的值。在內部循環中，只有x變化，每次變化1。要注意f(x+1,y)=f(x,y)+4，這是增量算法的基礎。在外部循環中，由計算f(x,y)變成計算f(x,y+1)，因此計算效率類似。由于在循環中 $\alpha$ 、 $\beta$ 、 $\gamma$ ?的變化增量是固定的，顏色c的變化也一樣，因此該算法也可以變為增量算法。例如，像素(x,y)到像素(x+1,y)的紅色值改變量，可以設為預先計算出的一個常量。三角形顏色插值的實例見圖

處理三角形邊上的像素

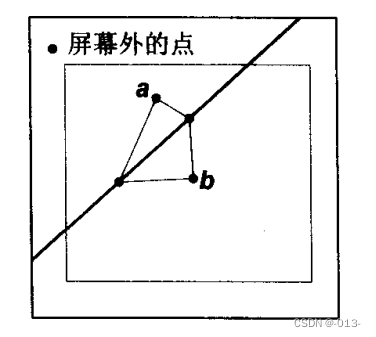
我們還沒有討論如何處理那些中心位于三角形邊上的像素。如果一個像素正好落在三角形的邊上,那么它同時還位于相鄰三角形的邊上。沒有明確的方式來確定該像素到底屬于哪個三角形。最壞的決定就是不繪制該像素，這時兩個三角形之間就會出現一個空隙。如果在兩個三角形上都繪制該像素，情況相對會好一點，但仍然不是個好辦法。如果三角形是透明的，會造成重復繪制。我們確實想把這樣的像素點歸于其中的一個三角形，并希望這是個簡單過程。只要做好選擇，無
論選定哪個三角形都沒有關系。應該注意到，屏幕外的任何點肯定位于要繪制的公共邊的一側。對兩個互不重看的三角形來說，不在公共邊上的頂點位于公共邊的相對兩側。這些頂點中正好有一個與屏幕外的點處在同一側(如下圖)。這個常識是做判斷的基礎。判斷p與q是否同號，可以通過判斷pq>0是否成立來實現，這種方法在多數情況下都是行之有效的方法。

注意這種判斷方法不是完美的，因為通過三角形邊的直線也許會正好通過屏幕外的那一點，但至少我們縮小了考慮范圍。選用屏幕外的哪一點是任意的，較好的選擇是(x,y)=(-1，-1)。需要對那些正好位于邊上的點進行核查，但對于完全在內部或者完全在外部的一般情況不應核查。所以有：

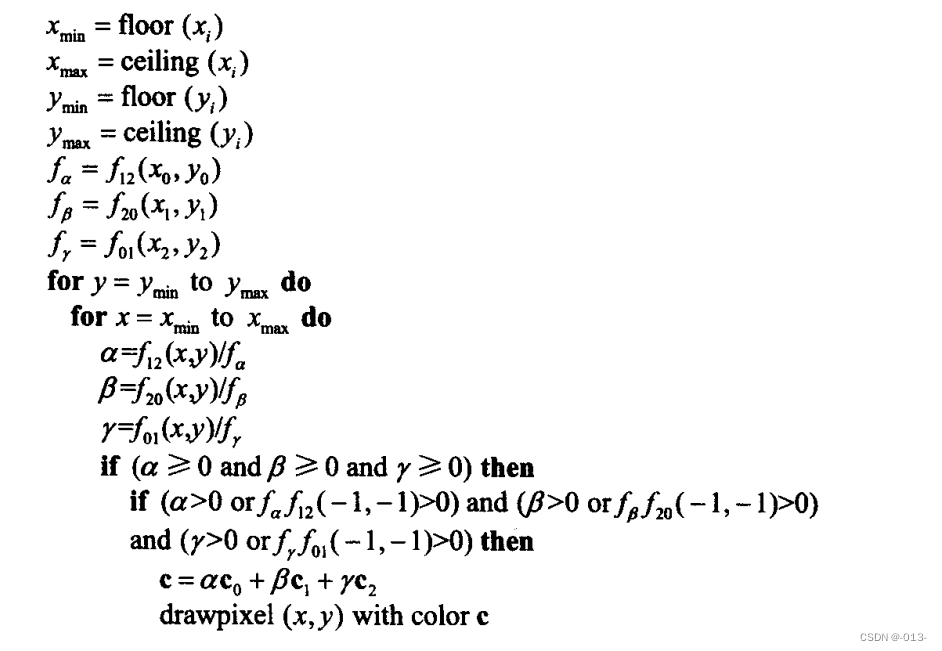
當對兩個三角形使用同樣的直線方程時，我們會希望上面的代碼能夠消除空隙和重復繪制。實際上，在調用三角形繪制函數時，只有當兩個公共頂點的順序是一樣時，直線方程才是一樣的。否則直線方程的符號就不同。這個問題取決于編譯器是否改變操作的順序。因此，如果想使算法穩健，應明白編譯器以及算術單元的細節。上面偽碼的前4行需要認真考慮，用以處理三角形的邊正好過像素中心的情況。
除了能把代碼改為增量形式外，還存在一些提前退出的可能。例如，如果是負的，那么就不必計算B或者v了。顯然這樣做能夠提高運算速度，對程序進行改進總是值得提倡的。額外的分支對流水操作和并行處理不利，而且會降低代碼的運行速度。所以，對于關鍵部分的代碼，應該嘗試各種優化方法。

以上代碼的另一個細節是，對于退化三角形，即 $f_{y} = 0$ 情況，上面的代碼可能會出現除數為0的現象。為了解決這個問題，應采用浮點誤差條件，或者增加其他判斷方式。

7.簡單的反走樣技術

前面講過的直線繪制和三角形繪制算法，普遍存在鋸齒現象。如果允許像素值變低或變高些(Crow，1978)，則可以減輕這種視覺上的不足。例如，對于白色背景上的一個黑色三角形如果一個像素的中心幾乎位于該三角形的內部，則可以將該像素設為黑白之間的顏色。圖1中上面的那條直線就是按這種方法繪出的。在實際應用中，這種模糊化處理可以改進視覺效果，尤
其是在動畫制作中。構造“無鋸齒”圖像的最直接方法就是采用盒式濾波器，將像素設置為盒式區域的平均顏色值。這就意味著，要把所有可繪制的實體都看作已經明確定義的區域。例如，圖2中的直線段就是一個矩形。第4章中討論更復雜的模糊化技術，這些技術可以改善外觀質量。像中點算法產生的鋸齒狀直線這樣的現象，是走樣(aliasing)造成的結果，該術語來自信號處理。因此，通過認真選擇像素值來避免鋸齒現象的技術，稱為反走樣(antialiasing)技術。盒式濾波器可以滿足多數情況的需要，適用于對視覺質量要求不是特別高的場合。

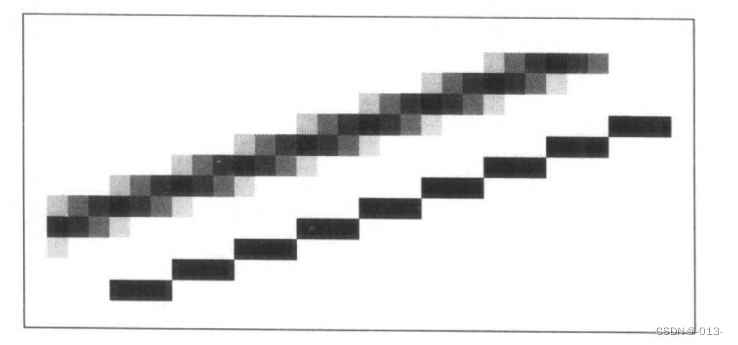
實現盒式濾波器反走樣的最容易辦法是，先建立高分辨率圖像，然后進行下采樣。例如，我們要處理一幅256x256的圖像，其中的直線寬度為1.2個像素。可以在1024x1024的屏幕上，對寬為4.8像素的直線段構成的矩形區域進行光柵化處理，然后對像素進行4x4平均，得到256x256的壓縮圖像。這是對實際圖像的近似盒式濾波，如果目標相對于像素間距不是特別小的話，這種方法的效果還是非常好的。