在數字信號處理技術中，傅里葉變換及其逆變換是一種信號時頻分析方法。該方法將信號的時域描述及頻域描述聯系在一起，時域信號可通過正變換轉變為頻域信號，頻域信號可通過逆變換轉變為時域信號進行分析。但傅里葉變換及其逆變換是一種信號的整體變換，要么完全在時域內進行分析處理，要么完全在頻域內進行分析處理，無法得到信號頻譜含量隨時間的變化規律，即傳統傅里葉變換及其逆變換存在不適用于非平穩信號、沒有局限性及時域與頻域分割的缺陷。要克服上述缺陷，就需要尋找聯合時頻方法。

1946年，GaborD.提出了短時傅里葉變換，該變換可將信號的時域分析和頻域分析結合起來，其變換結果既反映了信號的頻率內容，又反映了頻率內容隨時間變化的規律。短時傅里葉變換的過程為：用一個時寬足夠窄的窗函數與時間信號相乘，窗內的信號近似視為平穩信號，然后在窗內進行傅里葉變換，得到信號的瞬時頻譜。隨著截取窗在時間軸上移動，得到整個時間域上的頻譜。

短時傅里葉變換是一種線性的聯合時頻分析方法，其采用固定的窗函數對信號進行加窗處理，該變換克服了傳統傅里葉變換的缺陷，同時易于實現。與傅里葉分析不同，短時傅里葉變換中的窗函數種類繁多，為將短時傅里葉變換的效果最優化，窗函數的選取顯得尤為重要。實際應用的基本窗函數，主要分為以下類型：應用冪次時間函數的冪窗、應用三角時間函數的三角函數窗及應用指數時間函數的指數窗。

短時傅里葉變換中，采用窗函數對信號進行截取會造成頻譜泄露，即某一頻率的信號能量擴散到其相鄰頻率點。頻譜泄漏與窗函數頻譜的兩側旁瓣有關，從保持信號最大信息和消除旁瓣的綜合效果出發，窗函數選取的基本原則為：（1）盡可能使窗函數頻譜中的主瓣寬度足夠窄，以獲得較陡的過渡帶，能量盡可能集中在主瓣內，提高頻譜分析時的頻率分辨率；（2）旁瓣高度盡量小且隨頻率盡快衰減，以提高阻帶的衰減，減小頻譜分析時的泄露失真。但主瓣既窄，旁瓣又小衰減又快的窗函數很難找到，所以需要根據信號的性質和研究目的來選取合適的窗函數。

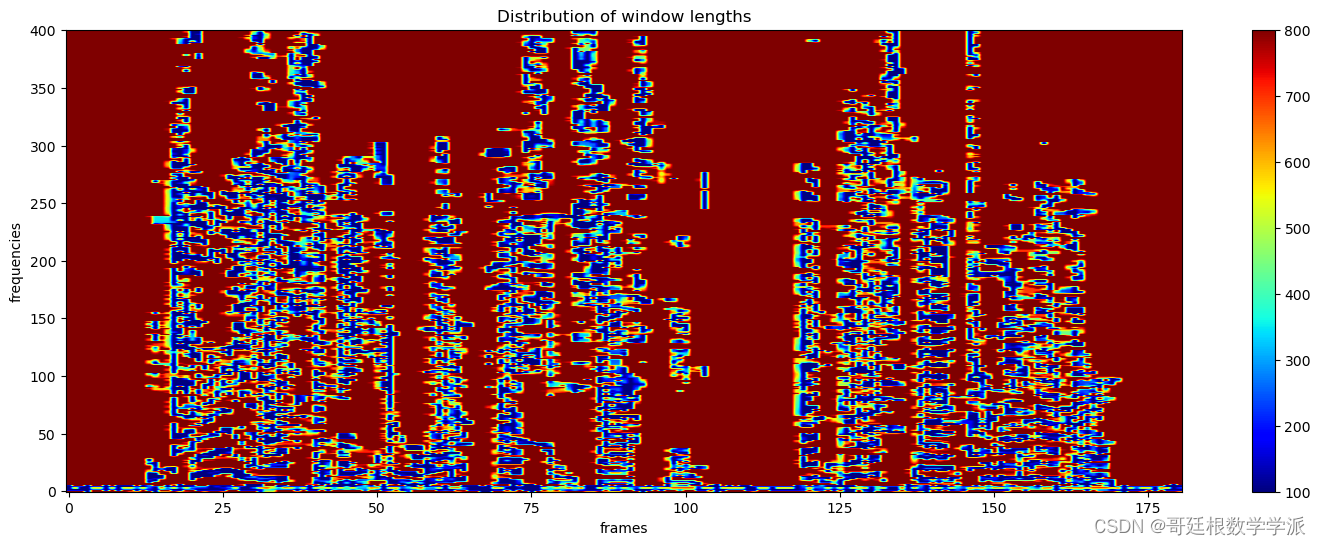
為了自適應的對窗長進行調整，提出一種基于梯度下降的自適應短時傅里葉變換，主要貢獻是窗口長度優化的新范例，包括修改STFT算子的定義，使窗長成為一個連續的參數，進而使得譜圖可以被微分，運行環境為Python，采用Jupyter Notebook文件格式。部分模塊如下：

from math import pi
import matplotlib.pyplot as plt
import numpy as np
import torch
import torchaudio

部分代碼如下：

sr = 1e4
t = torch.arange(0, 2.5, 1/sr)
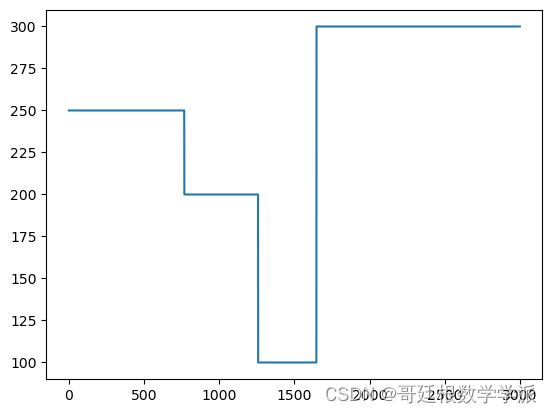
f = torch.sin(2*pi*t) * 1e2 + 1e2 * torch.ones_like(t) + 5e1 * t
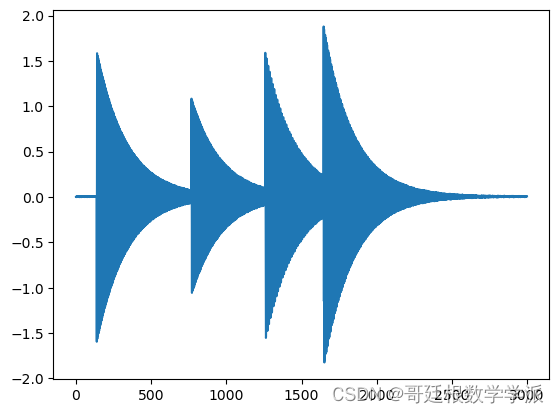
x = (torch.sin(torch.cumsum(f, dim=0) / 2e2) + 0.1 *torch.randn(t.shape))[None, :]
x += torch.sin(torch.cumsum(1e2*5 * torch.ones_like(t), dim=0) / 2e2)
x = x.to(device)
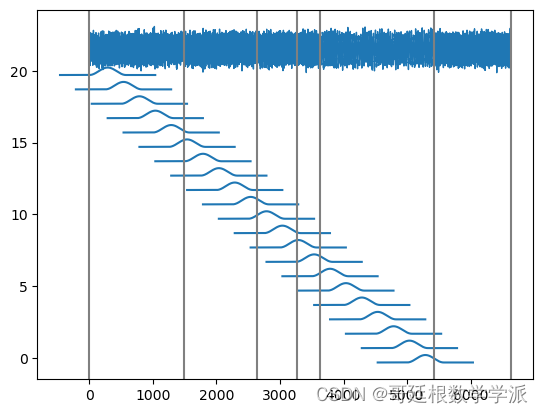
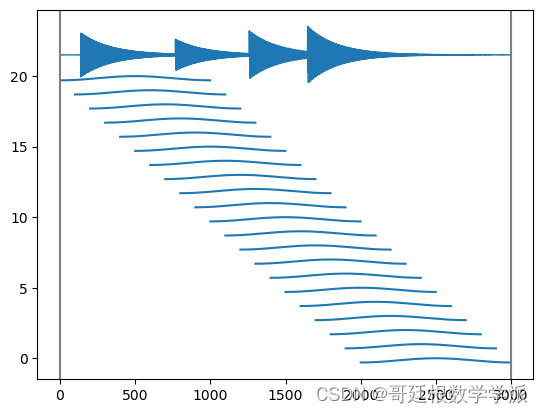
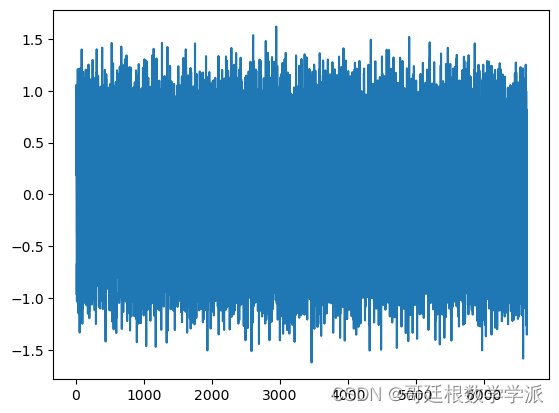
print(x.shape)plt.plot(f)spec = torchaudio.transforms.Spectrogram(n_fft=1_000, win_length=1_000, hop_length=100)(x.cpu())
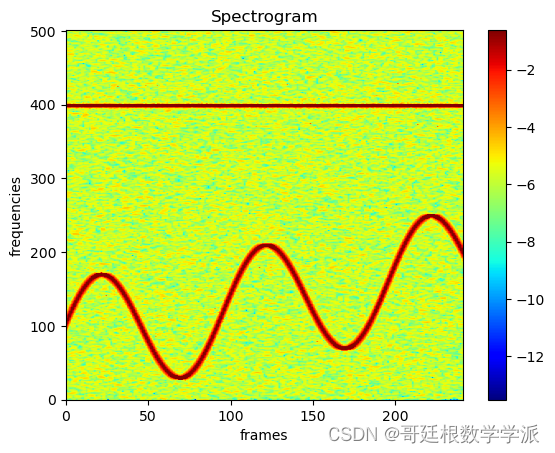
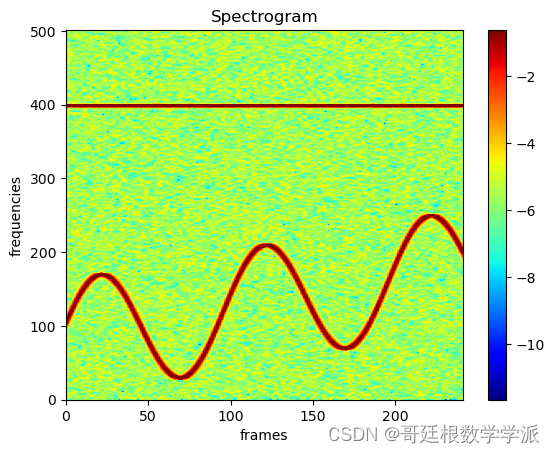
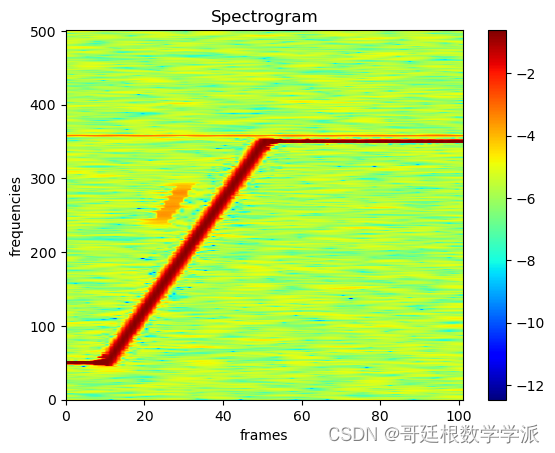
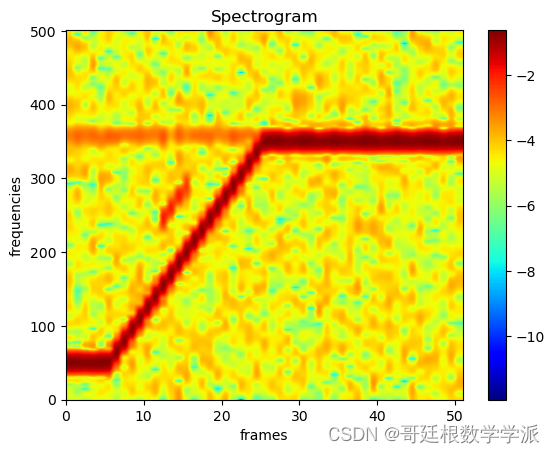
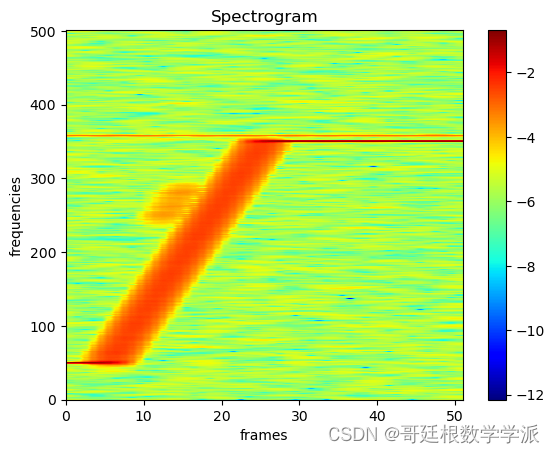
plt.imshow(spec[0].log().cpu(), aspect='auto', origin='lower', cmap='jet', extent=[0,spec.shape[-1], 0, spec.shape[-2]])
plt.ylabel('frequencies (Hz)', fontsize=18)
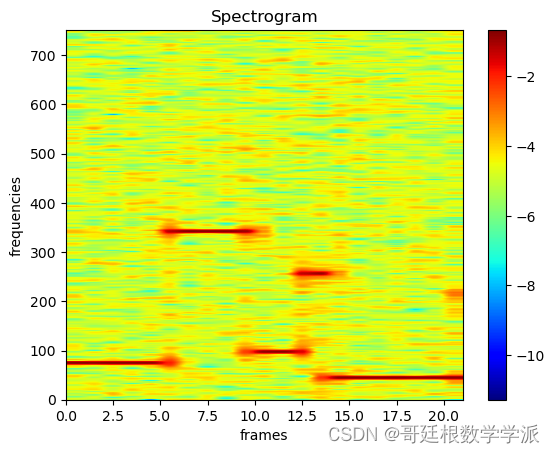
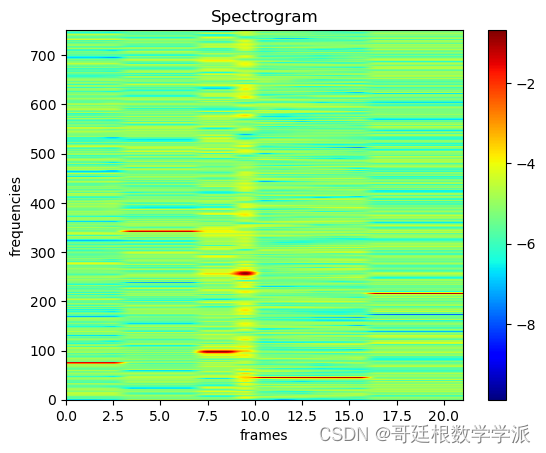
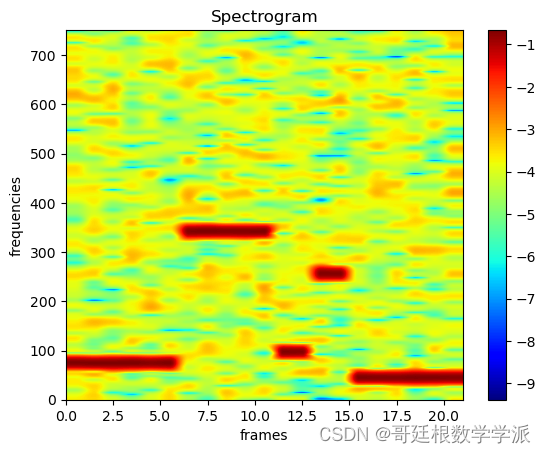
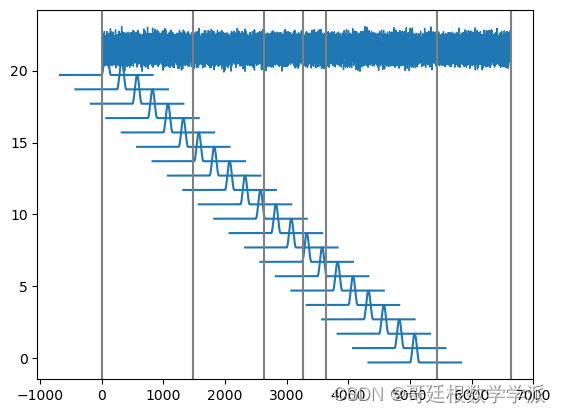
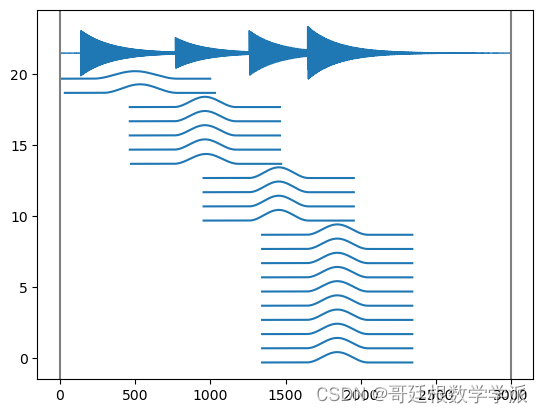
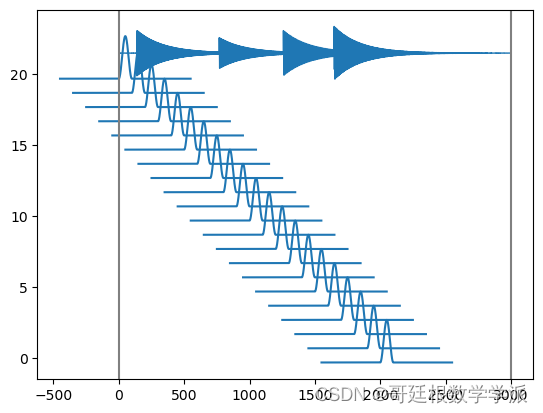
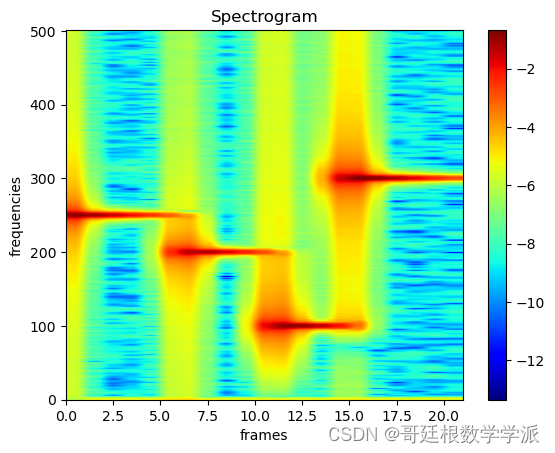
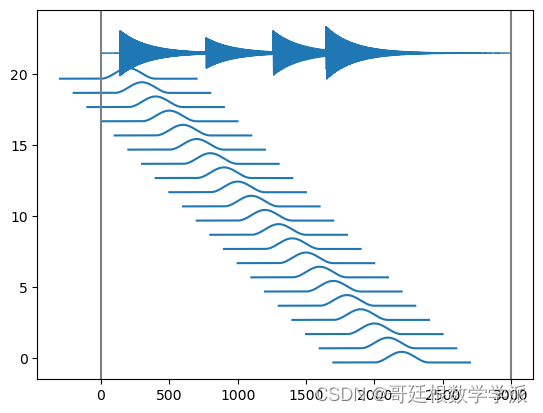
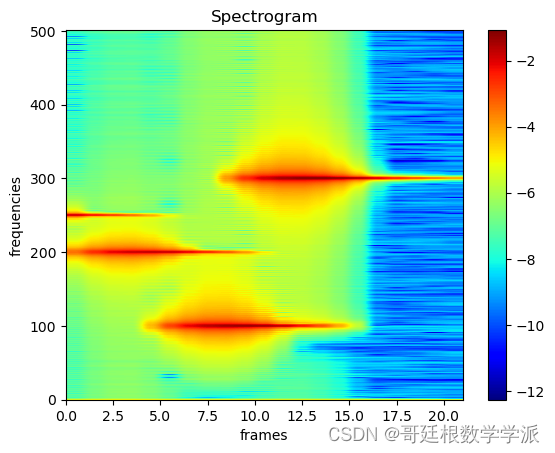
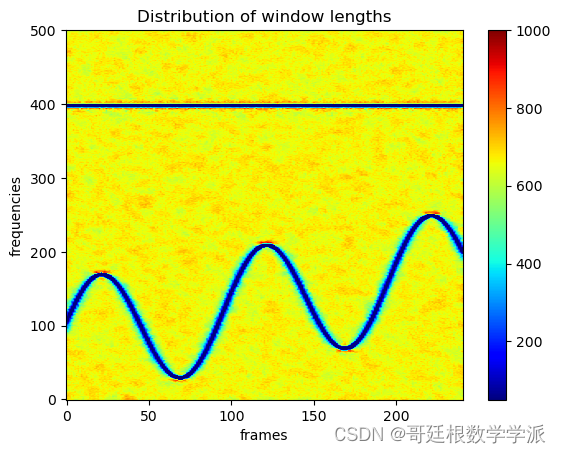
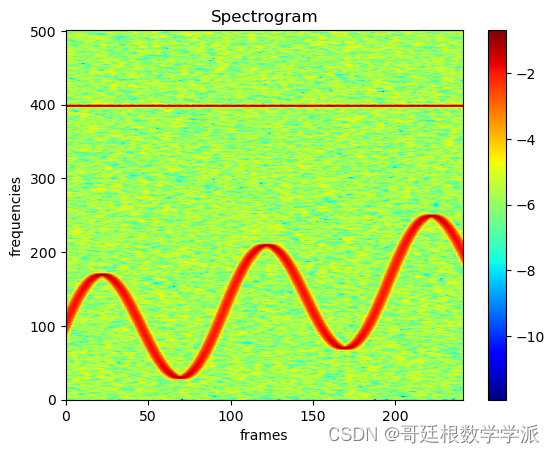
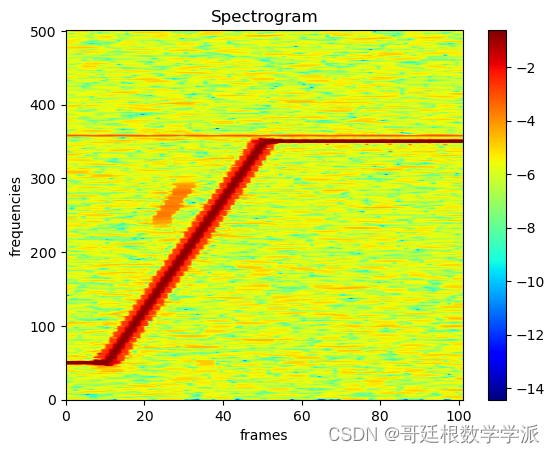
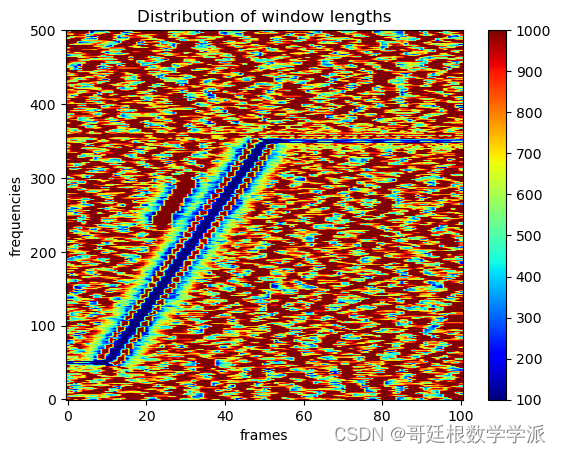
plt.xlabel('frames', fontsize=18)

出圖如下：

工學博士，擔任《Mechanical System and Signal Processing》審稿專家，擔任
《中國電機工程學報》優秀審稿專家，《控制與決策》，《系統工程與電子技術》，《電力系統保護與控制》，《宇航學報》等EI期刊審稿專家。

擅長領域：現代信號處理，機器學習，深度學習，數字孿生，時間序列分析，設備缺陷檢測、設備異常檢測、設備智能故障診斷與健康管理PHM等。