今天給大家分享的是樸素貝葉斯算法，這個算法在實際使用中不是很多，因為現在很多算法已經發展的很好，性能上也比樸素貝葉斯算法的好很多，因此在實際中我們其實看到在實際應用中樸素貝葉斯算法的使用已經比較少，即使出現，最終的效果也是不及其他算法的，但是作為簡單、基礎的算法之一，我們掌握該算法的原理還是非常有必要的，同時在實際論文研究中也經常會使用貝葉斯算法的改進版，所以大家可以多了解了解。

樸素貝葉斯算法是基于貝葉斯定理與特征條件獨立假設的分類方法。基本的思路就是給定訓練數據集，首先基于特征條件獨立假設學習輸入輸出的聯合概率分布；然后基于此模型，對給定的輸入x，利用貝葉斯定理求出后驗概率最大的輸出y。在介紹樸素貝葉斯算法之前，我們先做一些基礎知識的鋪墊——貝葉斯定理，該定理匯總比較重要的兩個數學公式就是先驗概率分布和條件概率分布，先驗概率分布公式如下：

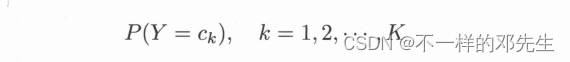
條件概率分布如下：

大家可以從公式中可以看出，先驗概率分布其實就是訓練數據中的不同類別數據占總體數據的比例（在實際中，頻率近似概率），條件概率分布就是指在確定數據是某個類別的條件下，樣本集X為指定值的概率，條件概率分布中的參數是非常多的，不僅涉及類別，還涉及特征以及特征的不同取值，假設表示第j個特征，該特征可能的取值有,j=1,2.....n,Y表示可取的類別，這樣的類別有K個，那么參數個數為，因此在實際中是不可取的。從而產生了樸素貝葉斯算法中對條件概率分布做出的條件獨立性假設，如果大家對獨立性理解不了的話，請上網搜索答案，條件獨立性假設如下：

大家可以將該公式和沒有獨立的公式進行對比，可以發現，獨立之后的結果就是可特征進行了拆分，條件獨立假設等于是說分類的特征在類確定的條件下都是條件獨立的。這一假設使樸素貝葉斯算法變得簡單，但是會損失一定的分類準確率。

根據訓練數據，模型學習到了先驗分布和條件獨立概率分布，從而可以根據輸入的X計算得出后驗概率分布,該公式表示在知道特征X的情況下，類別為的概率，因此我們將該結果最大的類輸出即可。后驗概率公式為：

再結合特征條件獨立性假設，公式變換為：

綜上，樸素貝葉斯分類器可以表示為：

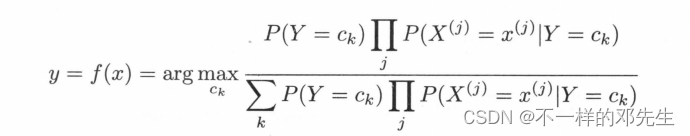
該公式表示我們將數據特征X使用樸素貝葉斯算法公式計算了在不同類別上的后驗概率，最終選擇這些概率中最大的一個概率，將其對應的類別輸出，即判定為特征X對應的類別，在該公式中由于分母都是相同的，分母為什么是相同的，大家可以去網上查看簡化版的好理解，實際在計算不同類別的時候，大家分母上的計算都是使用了所有的類別和所有的特征進行計算，因此在分母結果都是一樣，從而該公式可以簡化為：

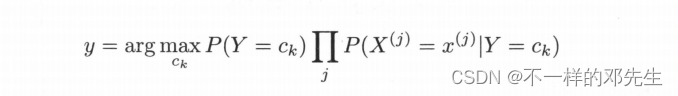
?大家可能會比較好奇，為什么這里需要使用后驗概率最大化來選擇類結果，后驗概率最大化代表類什么實際含義以及這個選擇是怎么來的？大家如果學習過其他算法其實都了解，每一種算法都會有一個目標函數，樸素貝葉斯算法也不例外，假設存在一個0-1損失函數，表達式為：

?期望風險函數為：

取條件期望得：

?

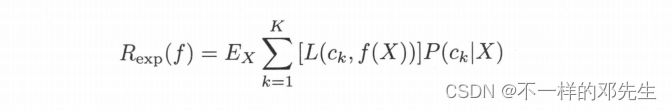
我們的目標就是追求期望損失最小話，從而可得 :

?我相信大家對這幾個等式應該還是比較好理解，可能稍微有難度就是第二等式，為什么直接將損失函數轉換為類別不等的條件概率，是因為在上一個式子損失函數中，只有類別不等的時候我們才會存在損失函數同時損失函數為1，因此，我們下面直接轉換成在確定樣本X的條件下，類別不等的概率，最終的結果就轉換成我們前面說的后驗概率最大化，從而我們后驗概率最大化是為了追求我們期望損失最小化得出來的。

樸素貝葉斯算法的總結如下：

我先使用簡單直觀的理解給大家講解一下樸素貝葉斯算法的流程，后續將會使用一個實際案例給大家展示，我們首先計算先驗概率，即不同類別在總數據中所占比例，接著，計算條件獨立概率分布，即在不同類別下，不同特征取某個特征值的概率，遍歷所有類別、所有特征以及所有特征取值，?最后新的輸入數據，計算其所有特征后驗概率，將最大后驗概率最大的類別作為該數據的類別。??

fbs	restecg	output
1	0	1
0	1	1
0	0	0
0	1	0

以上是給出的訓練數據，前兩列代表特征，最后一列代表分類，我們將會給出測試集數據（1，1）作為案例用于算法測試，算法運行結果如下：

從計算數據可以看出，最終的結果判定為1類別。在這個實際計算過程中，大家看到了以上我們使用極大似然估計得出的概率可能為0，為了處理這種情況，于是對樸素貝葉斯算法進行了改進，得到了貝葉斯估計，條件概率的貝葉斯估計概率公式為：

?和樸素貝葉斯算法相比就是在分子分母上加上了一個正數>=0,確保了計算出的概率不會等于0，當==0時就是樸素貝葉斯使用的極大似然估計，當==1時就是拉普拉斯平滑，貝葉斯估計的先驗分布為：

大家也可以根據貝葉斯定理的前驗分布和條件概率分布求出某個數據特征的后驗概率，從而可以得出數據的類別，大家可以指定==1，即拉普拉斯平滑系數計算一下上面的案例，這里我就不再計算結果了，以上就是貝葉斯算法相關全部內容，大家如果對其他內容感興趣，關注公眾號“明天科技屋”，?更多精彩內容為您推薦！！！