46.全排列
力扣題目鏈接(opens new window)
給定一個 沒有重復 數字的序列，返回其所有可能的全排列。
示例:
- 輸入: [1,2,3]
- 輸出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
遞歸終止條件：當收集元素的數組path的大小達到和nums數組一樣大的時候，說明找到了一個全排列，也表示到達了葉子節點。
而used數組，其實就是記錄此時path里都有哪些元素使用了，一個排列里一個元素只能使用一次。
- 每層都是從0開始搜索而不是startIndex
- 需要used數組記錄path里都放了哪些元素了
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此時說明找到了一組if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i] == true) continue; // path里已經收錄的元素，直接跳過used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};47.全排列 II
力扣題目鏈接(opens new window)
給定一個可包含重復數字的序列 nums ，按任意順序 返回所有不重復的全排列。
示例 1：
- 輸入：nums = [1,1,2]
- 輸出： [[1,1,2], [1,2,1], [2,1,1]]
示例 2：
- 輸入：nums = [1,2,3]
- 輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
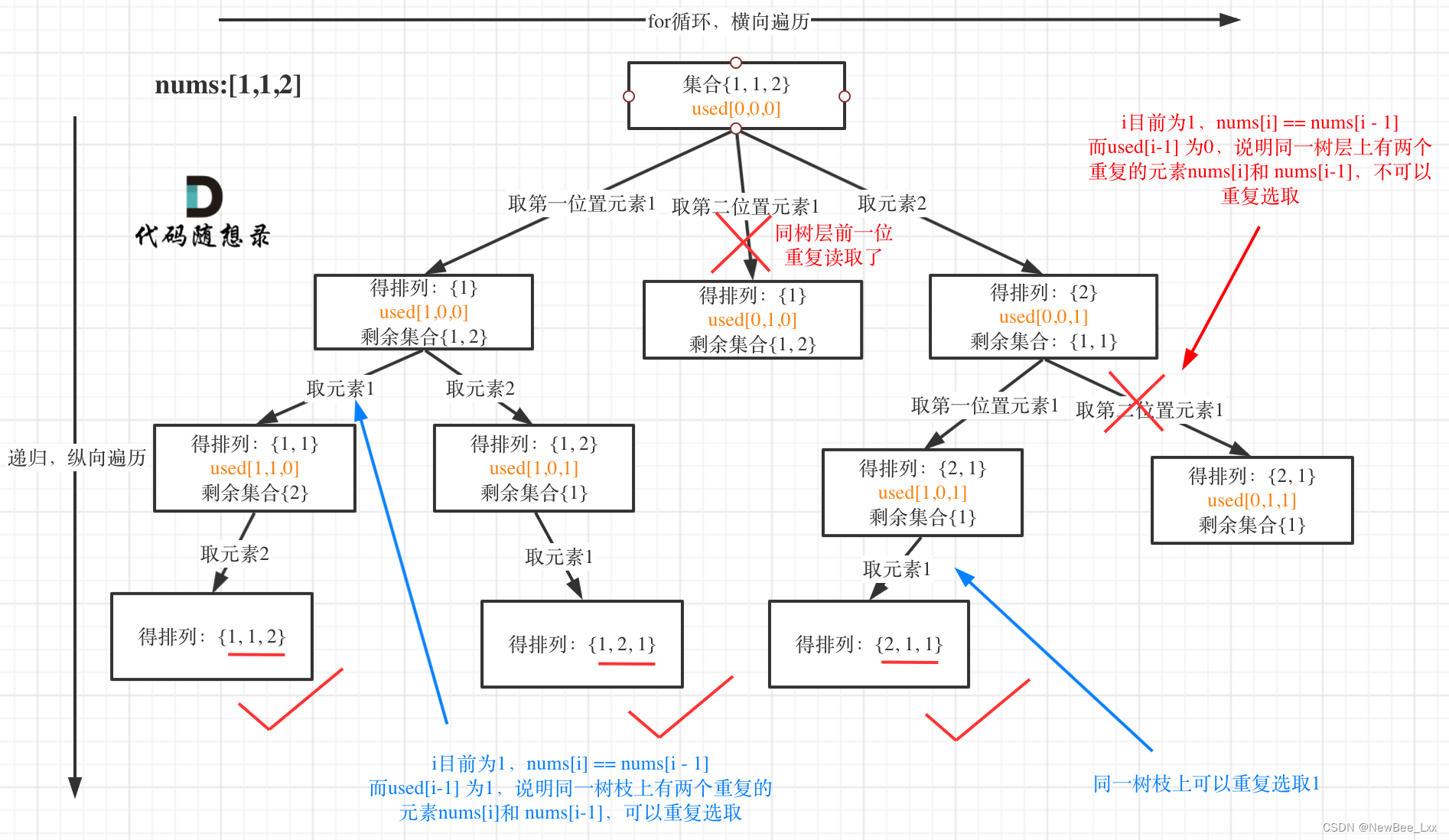
?先排序，樹層去重，123，132可以出現所以不用index，一次排列用過的元素不能再用了 所以設置used數組
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此時說明找到了一組if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {// used[i - 1] == true，說明同一樹枝nums[i - 1]使用過// used[i - 1] == false，說明同一樹層nums[i - 1]使用過// 如果同一樹層nums[i - 1]使用過則直接跳過if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}if (used[i] == false) {used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 排序vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};
51. N皇后
力扣題目鏈接
?
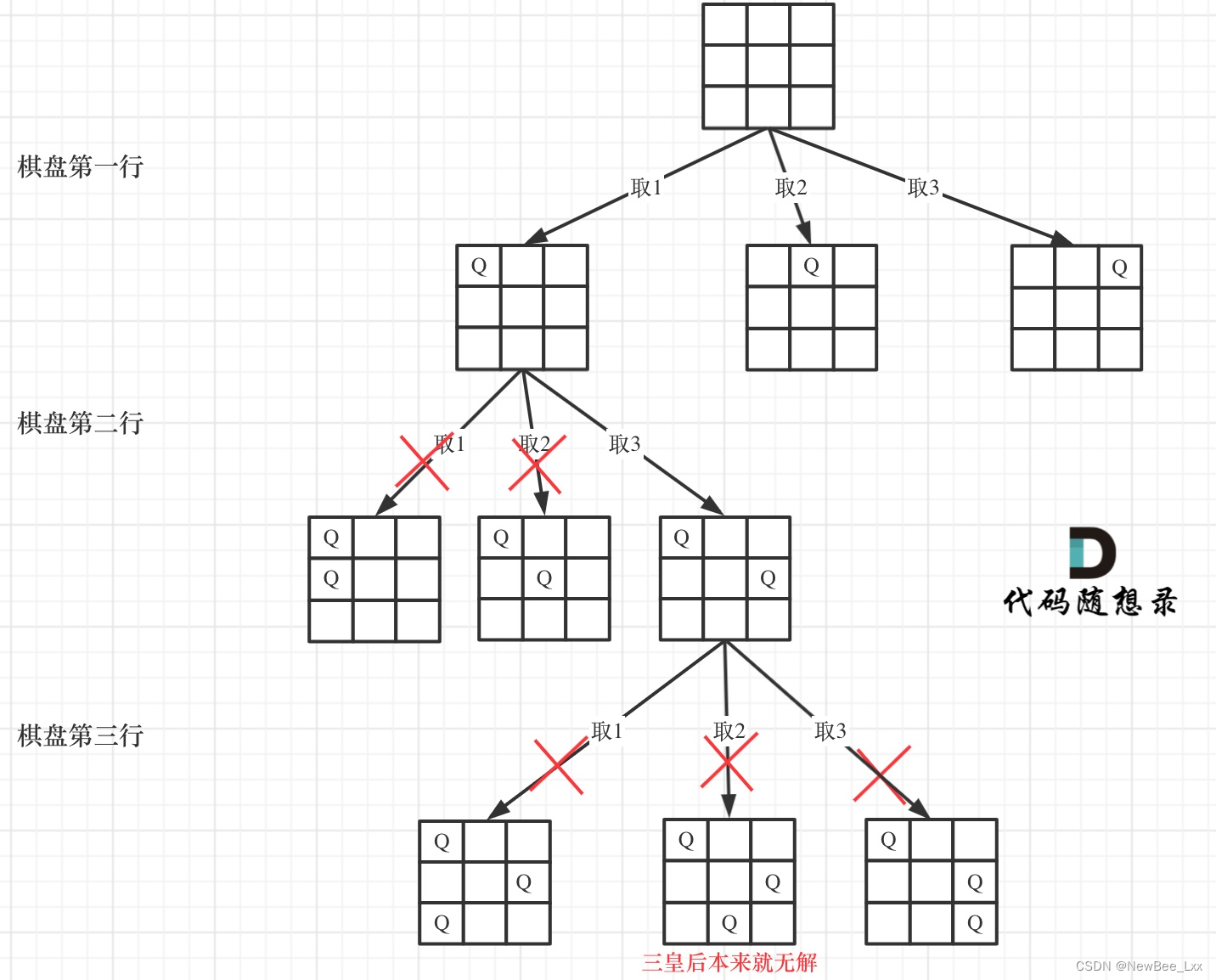
- 驗證棋盤是否合法
按照如下標準去重：
- 不能同行
- 不能同列
- 不能同斜線 （45度和135度角）
回溯三部曲：
（1）確定參數及返回值：返回類型為void型，參數n為棋盤大小，row記錄到第幾層。
（2）返回條件：當遍歷到棋盤的最后一層，就可以收集結果并返回。
（3）單層搜索的邏輯：每一行每一列進行遍歷確定皇后的位置。
class Solution {
private:
vector<vector<string>> result;
// n 為輸入的棋盤大小
// row 是當前遞歸到棋盤的第幾行了
void backtracking(int n, int row, vector<string>& chessboard) {if (row == n) {result.push_back(chessboard);return;}for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) { // 驗證合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][col] = '.'; // 回溯，撤銷皇后}}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {// 檢查列for (int i = 0; i < row; i++) { // 這是一個剪枝if (chessboard[i][col] == 'Q') {return false;}}// 檢查 45度角是否有皇后for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 檢查 135度角是否有皇后for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;
}
public:vector<vector<string>> solveNQueens(int n) {result.clear();std::vector<std::string> chessboard(n, std::string(n, '.'));backtracking(n, 0, chessboard);return result;}
};?
)